<< 4.2 Коэффициент теплопро...
| Оглавление |
4.4 Критическая светимость >>
Зависимость 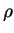 и и 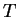 от радиуса определяется уравнениями: от радиуса определяется уравнениями:
1)
 -- уравнение гидростатики, -- уравнение гидростатики,
2)
 -- уравнение
теплопроводности, где -- уравнение
теплопроводности, где
 -- светимость, т.е. полный поток энергии
через сферу радиуса -- светимость, т.е. полный поток энергии
через сферу радиуса 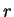 . Так как . Так как
 , перепишем последнее
уравнение в виде , перепишем последнее
уравнение в виде

Если бы ядерная энергия каждой единицы массы звезды
 эрг эрг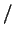 г г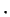 с с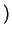 выделялась одинаково, так что выделялась одинаково, так что
 const
по звезде и const
по звезде и
 , то мы получили бы, что , то мы получили бы, что
 Поскольку приближенно
Поскольку приближенно
 |
(4.3) |
мы получим решение, положив, например,
 const const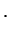
Несколько десятков лет назад, когда мало знали об источниках ядерной энергии,
астрофизики занимались задачами подобного рода, однако сейчас это представляет
чисто исторический интерес.
Вблизи поверхности звезды
 -- полная светимость звезды и -- полная светимость звезды и
 это хорошее приближение потому, что постоянно выделение энергии
это хорошее приближение потому, что постоянно выделение энергии
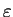 ,
а потому, что у поверхности ,
а потому, что у поверхности  . .
При   , ,  и и
 const const . Из (4.3) получим . Из (4.3) получим
 const, а из уравнения гидростатики const, а из уравнения гидростатики
 const const имеем
имеем
 const const . Из . Из
 const следует const следует
 const const . Таким образом, независимо от того, как распределены
источники ядерной энергии вблизи центра звезды, следует асимптотическое распределение . Таким образом, независимо от того, как распределены
источники ядерной энергии вблизи центра звезды, следует асимптотическое распределение
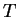 и и 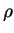 вблизи поверхности. Заметим только, что на краю вблизи поверхности. Заметим только, что на краю  , а , а
 . Поэтому наши асимптотики верны при . Поэтому наши асимптотики верны при  , где , где  определяется
соотношением определяется
соотношением
 т.е. не в атмосфере и не в короне.
т.е. не в атмосфере и не в короне.
<< 4.2 Коэффициент теплопро...
| Оглавление |
4.4 Критическая светимость >>
Посмотреть комментарии[2]
|

