<< 3.3 Кинетика фотонов и
| Оглавление |
3.5 Рассеяние излучения на ... >>
Заряд (электрон), движущийся равномерно и прямолинейно, очевидно, ничего не излучает
(чтобы в этом убедиться, достаточно перейти в систему отсчета, где он покоится).
Из классической электродинамики известно, что количество энергии, излучаемой зарядом
в единицу времени, определяется его ускорением:
 Подчеркнем, что эта формула относится к одному заряду. Если ускоряются два жестко
связанных электрона, то
Подчеркнем, что эта формула относится к одному заряду. Если ускоряются два жестко
связанных электрона, то 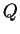 возрастает в 4 раза (так как возрастает в 4 раза (так как  ). Таким образом,
нельзя просто суммировать ). Таким образом,
нельзя просто суммировать 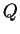 от различных зарядов. от различных зарядов.
Ниже мы будем рассматривать излучение электрона при ускорении его во внешнем
электрическом поле, скажем, в кулоновском поле иона. Вдали электрон движется
практически с постоянной скоростью. Ускорение электрона максимально при пролете
на минимальном расстоянии от иона. Очевидно, при этом максимально и излучение.
Нас будет интересовать и спектральный состав излучения
 , где , где  -- фурье-компонента ускорения. -- фурье-компонента ускорения.
Займемся излучением длинных волн. Фурье-компонента ускорения
 Если
Если
 (длинные волны) (длинные волны)
 т.е.
т.е.
 равно изменению скорости за время полета и не зависит от равно изменению скорости за время полета и не зависит от 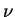 . Тогда при одном столкновении в единичном интервале частот излучается энергия . Тогда при одном столкновении в единичном интервале частот излучается энергия
![$\displaystyle Q_\nu\,\left[{\mbox{эрг}\over \mbox{Гц}}\right]={4\over 3}\,e^2\,{(\Delta x)^2\over c^3}.$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img685.gif) |
(3.3) |
Подчеркнем еще раз, что это выражение справедливо только при
 , где , где
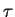 -- длительность события (столкновения) (рассматриваем длинные волны).
Заметим, что размерность -- длительность события (столкновения) (рассматриваем длинные волны).
Заметим, что размерность  в формуле (3.3) изменилась на
с в формуле (3.3) изменилась на
с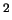 по сравнению с размерностью
по сравнению с размерностью
![$ Q\,\left[{\mbox{эрг}\over \mbox{с}}\right]$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img688.gif) , так как
мы перешли сначала на единичный интервал частот и, кроме того, рассматриваем энергию,
излученную не в секунду, а за все время пролета. , так как
мы перешли сначала на единичный интервал частот и, кроме того, рассматриваем энергию,
излученную не в секунду, а за все время пролета.
 |
| Рис. 18. |
Легко подсчитать изменение импульса электрона, пролетающего в поле иона, первоначально
имеющего скорость 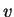 и прицельный параметр и прицельный параметр  (рис. 18): (рис. 18):
 откуда
откуда

Пусть на ион с бесконечности падает пучок электронов со скоростью 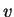 и плотностью и плотностью
 . Через кольцо площадью . Через кольцо площадью  около поля иона проходит около поля иона проходит
 электронов в секунду. Каждый из них в единичном интервале частот излучает
электронов в секунду. Каждый из них в единичном интервале частот излучает  .
Если в 1
см .
Если в 1
см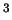 находится находится  ионов, то полный поток энергии, излучаемый
в единицу времени, очевидно, равен интегралу (логарифмический множитель опускаем) ионов, то полный поток энергии, излучаемый
в единицу времени, очевидно, равен интегралу (логарифмический множитель опускаем)
 Из квантовой механики известно, что квант частотой
Из квантовой механики известно, что квант частотой 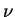 может излучить только
электрон, имеющий энергию больше может излучить только
электрон, имеющий энергию больше
 . Поэтому в полное выражение
войдет множитель . Поэтому в полное выражение
войдет множитель

![$\displaystyle J_\nu={32\pi\over 3}\,{\left({2\pi\,m\over {3kT}}\right)}^{1/2}\,...
...^{-{h\nu\over {kT}}}\;\left[{\mbox{эрг}\over {\mbox{см}^3
\mbox{с Гц}}}\right]
$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img700.gif) (формула тормозного или
(формула тормозного или  -излучения). В этой формуле учтено, что электроны
имеют максвелловское распределение по скоростям с температурой -излучения). В этой формуле учтено, что электроны
имеют максвелловское распределение по скоростям с температурой 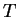 . Как видим,
число квантов с . Как видим,
число квантов с  экспоненциально мало. Это связано с тем, что большие
кванты излучаются электронами с большими энергиями, сосредоточенными в ``хвосте''
максвелловского распределения. экспоненциально мало. Это связано с тем, что большие
кванты излучаются электронами с большими энергиями, сосредоточенными в ``хвосте''
максвелловского распределения.
При данном объемном коэффициенте  изменение интенсивности изменение интенсивности 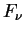 в прозрачной
среде, очевидно, определяется уравнением в прозрачной
среде, очевидно, определяется уравнением
 где
где 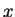 -- координата вдоль произвольного направления -- координата вдоль произвольного направления 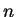 . Прозрачный источник (
малы поглощение и индуцированное излучение) дает одну и ту же освещенность в любой
точке сферы с радиусом много больше размеров источника независимо от формы источника.
В общем случае с учетом индуцированного излучения и поглощения изменение интенсивности
вдоль определенного направления выражается уравнением . Прозрачный источник (
малы поглощение и индуцированное излучение) дает одну и ту же освещенность в любой
точке сферы с радиусом много больше размеров источника независимо от формы источника.
В общем случае с учетом индуцированного излучения и поглощения изменение интенсивности
вдоль определенного направления выражается уравнением
 где
где
 см см![$ ^{-1}]$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img707.gif) -- коэффициент поглощения. -- коэффициент поглощения.
При полном термодинамическом равновесии
 .
Получаем, что отношение объемного коэффициента излучения вещества .
Получаем, что отношение объемного коэффициента излучения вещества  к его
коэффициенту поглощения к его
коэффициенту поглощения  есть универсальная функция есть универсальная функция 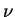 и и 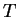 (закон
Кирхгофа): (закон
Кирхгофа):
 Таким образом, если вычислено
Таким образом, если вычислено  , то , то  находится элементарно, и для
свободно-свободных находится элементарно, и для
свободно-свободных  -переходов получаем -переходов получаем
![$\displaystyle a_\nu={4\over 3}\,{\left({2\pi\over {3kTm}}\right)}^{1\over 2}\,{...
...{hcm\,\nu^3}}={3,7\cdot 10^8Z^2N_ZN_e\over {\nu^3\sqrt{T}}}\;[\mbox{см}^{-1}].
$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img712.gif) Объединим в правой части уравнения переноса члены, отвечающие индуцированному
излучению и поглощению, так как оба они пропорциональны неизвестной функции координат
-- интенсивности излучения
Объединим в правой части уравнения переноса члены, отвечающие индуцированному
излучению и поглощению, так как оба они пропорциональны неизвестной функции координат
-- интенсивности излучения 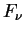 (поскольку (поскольку
 ). В члене индуцированного
испускания ). В члене индуцированного
испускания
 выразим выразим  через коэффициент поглощения через коэффициент поглощения  ,
тогда правая часть примет вид ,
тогда правая часть примет вид
 . .
Отсюда видно, что вынужденное испускание можно трактовать как некое уменьшение
поглощения: часть квантов как бы поглощается и тут же испускается с той же частотой
и в том же направлении с вероятностью
 . Физически такие акты никак
себя не проявляют и их можно вообще исключить из рассмотрения, вводя . Физически такие акты никак
себя не проявляют и их можно вообще исключить из рассмотрения, вводя
 Уравнение переноса принимает вид
Уравнение переноса принимает вид
 и взаимодействие излучения с веществом можно представить так, как будто существует
только спонтанное испускание и эффективное поглощение, описываемое коэффициентом
и взаимодействие излучения с веществом можно представить так, как будто существует
только спонтанное испускание и эффективное поглощение, описываемое коэффициентом
 . .
Коэффициент истинного поглощения
 , но при , но при  эффективное
поглощение эффективное
поглощение
 и в равновесии это дает рэлей-джинсовскую формулу
для интенсивности и в равновесии это дает рэлей-джинсовскую формулу
для интенсивности
 (коэффициент излучения (коэффициент излучения
 при при  фактически постоянен). Используя закон Кирхгофа фактически постоянен). Используя закон Кирхгофа
 , запишем в общем случае уравнение переноса в виде , запишем в общем случае уравнение переноса в виде
 Это уравнение записано для координаты, изменяющейся вдоль луча зрения. Из него
видно, что, если при
Это уравнение записано для координаты, изменяющейся вдоль луча зрения. Из него
видно, что, если при
 , то сначала, при малых , то сначала, при малых
 стремится к
стремится к
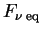 линейно: линейно:
 , а затем при , а затем при
 быстро устанавливается равновесие, при котором быстро устанавливается равновесие, при котором
 . Если
размеры излучающего облака (слоя) . Если
размеры излучающего облака (слоя) 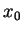 меньше меньше  , то оно является оптически
тонким и интенсивность его излучения всегда меньше равновесной в , то оно является оптически
тонким и интенсивность его излучения всегда меньше равновесной в
 раз.
Полный поток энергии, излучаемой такими облаками, пропорционален раз.
Полный поток энергии, излучаемой такими облаками, пропорционален
 . Введем средний коэффициент поглощения . Введем средний коэффициент поглощения
 тогда
тогда
 Средний коэффициент поглощения для тормозного механизма, очевидно, равен
Средний коэффициент поглощения для тормозного механизма, очевидно, равен
 см см![$\displaystyle ^{-1}].
$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img739.gif) Соответствующая средняя длина свободного пробега фотона
Соответствующая средняя длина свободного пробега фотона
 см см![$\displaystyle ].
$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img741.gif) Причем, если плазма содержит смесь ионов с зарядами
Причем, если плазма содержит смесь ионов с зарядами  и атомными массами и атомными массами  ,
то ,
то

 где
где  -- весовая доля данного иона. -- весовая доля данного иона.
 |
| Рис. 19. |
Рассмотрим процесс установления равновесия между веществом и излучением для однородной
неограниченной среды, в которой в начальный момент  излучение отсутствовало,
а вещество было мгновенно нагрето до температуры излучение отсутствовало,
а вещество было мгновенно нагрето до температуры 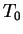 . Очевидно, что прежде всего
это равновесие установится на низких частотах, так как . Очевидно, что прежде всего
это равновесие установится на низких частотах, так как
 . С
течением времени равновесие будет устанавливаться при больших
значениях . С
течением времени равновесие будет устанавливаться при больших
значениях 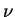 (см. рис. 19). (см. рис. 19).
<< 3.3 Кинетика фотонов и
| Оглавление |
3.5 Рассеяние излучения на ... >>
Посмотреть комментарии[2]
|

