<< 3.1 Введение
| Оглавление |
3.3 Кинетика фотонов ... >>
Пусть 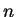 -- число фотонов в клетке фазового пространства, т.е. число заполнения,
которое безразмерно. Для ``ящика'' данного объема можно говорить о числе состояний.
Если состояний много, то число уровней в объеме -- число фотонов в клетке фазового пространства, т.е. число заполнения,
которое безразмерно. Для ``ящика'' данного объема можно говорить о числе состояний.
Если состояний много, то число уровней в объеме 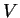 и в импульсном объеме и в импульсном объеме  есть
есть
 Тогда плотность числа фотонов
Тогда плотность числа фотонов
 см см![$\displaystyle ^{-3}],$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img582.gif) |
(3.1) |
где коэффициент 2 учитывает два возможных состояния с разными поляризациями.
Известно, что импульс фотона  связан с волновым вектором связан с волновым вектором  формулой
Де Бройля формулой
Де Бройля

Подставляя это выражение в формулу (3.1), получим более наглядное выражение
для плотности числа фотонов
 Поскольку
Поскольку
 , очевидна размерность , очевидна размерность
  и, кроме того, исчезает постоянная Планка и, кроме того, исчезает постоянная Планка  , которая была важна
только при подсчете числа состояний. , которая была важна
только при подсчете числа состояний.
В сферической системе координат
 В случае сферической симметрии
В случае сферической симметрии
 и и
 где
где 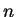 -- функция только от -- функция только от
 . .
Поскольку энергия одного фотона
 то плотность энергии излучения (фотонного газа)
то плотность энергии излучения (фотонного газа)

Кроме плотности энергии
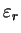 важной характеристикой является спектральная
интенсивность излучения важной характеристикой является спектральная
интенсивность излучения
![$ F_\nu\;([F_\nu]=$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img597.gif) эрг эрг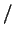 см см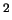 с Гц стер с Гц стер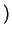 -- величина, которая при отсутствии поглощения или рассеивания не
зависит от расстояния до источника. Из наблюдений всегда получается -- величина, которая при отсутствии поглощения или рассеивания не
зависит от расстояния до источника. Из наблюдений всегда получается 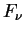 , а
в физику дела входит число заполнения , а
в физику дела входит число заполнения 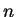 . .
Получим связь между 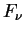 и и 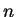 : :
 (при этом мы использовали, что
(при этом мы использовали, что
 ). ). 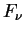 имеет смысл энергии,
проходящей через площадку имеет смысл энергии,
проходящей через площадку  в единицу времени в единичном интервале частот,
поэтому в единицу времени в единичном интервале частот,
поэтому
![$ [F_\nu]=$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img602.gif) эрг эрг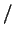 см см c c Гц. Гц.
В общем случае (и при отсутствии равновесия) связь между
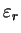 и и 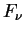 дается формулой
дается формулой

<< 3.1 Введение
| Оглавление |
3.3 Кинетика фотонов ... >>
Посмотреть комментарии[2]
|

