<< Титульный лист
| Оглавление |
1.2 Основные формулы фотометрии >>
1. Основные понятия
| ...толпы светов я увидел вдруг, |
| Залитые лучами огневыми ... |
| Данте. Рай, песнь 23 |
| (перевод М.Лозинского) |
|
Разделы
Пусть на верхнюю границу земной атмосферы за время 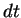 от
звезды приходит некоторое количество световой энергии от
звезды приходит некоторое количество световой энергии 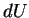 и
падает нормально на площадку площадью и
падает нормально на площадку площадью 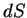 . Величина . Величина
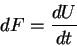 |
(1.1) |
называется световым потоком и имеет размерность мощности. С
помощью фотометра на телескопе мы измеряем именно световой поток.
Световой поток, проходящий через единицу площади,
называется освещенностью 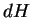 и имеет размерность мощности на
см и имеет размерность мощности на
см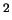
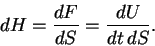 |
(1.2) |
Монохроматическая освещенность 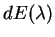 , т.е. освещенность
отнесенная к узкому интервалу длин волн , т.е. освещенность
отнесенная к узкому интервалу длин волн 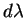 , называется удельной
освещенностью и обычно имеет размерность
эрг/(ссм , называется удельной
освещенностью и обычно имеет размерность
эрг/(ссм
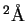 ) )
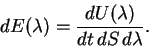 |
(1.3) |
Если интервал длин волн выражать не в ангстремах, а в сантиметрах, то
величина приобретает размерность эрг с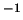 см см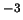 . Согласно ГОСТу она называется спектральной
плотностью энергетической освещенности. В этих величинах обычно
представляются данные в спектрофотометрических каталогах. Астрономы
обычно называют функцию . Согласно ГОСТу она называется спектральной
плотностью энергетической освещенности. В этих величинах обычно
представляются данные в спектрофотометрических каталогах. Астрономы
обычно называют функцию 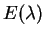 распределением энергии в
спектре. Величину распределением энергии в
спектре. Величину
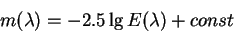 |
(1.4) |
мы будем называть монохроматической звездной величиной. Чтобы
эта величина приходилась на привычный нам интервал чисел (тот
самый, который выбрал давным-давно Гиппарх), в формуле (1.4)
предусмотрена константа.
<< Титульный лист
| Оглавление |
1.2 Основные формулы фотометрии >>
Написать комментарий
|

