Документ взят из кэша поисковой машины. Адрес оригинального документа : http://www.nature.web.ru/db/msg.html?mid=1158396&uri=s6node2.html
Дата изменения: Unknown
Дата индексирования: Mon Apr 11 14:47:35 2016
Кодировка: Windows-1251
Научная Сеть >> "Тригонометрия" И.М. Гельфанд, С.М. Львовский, А.Л. Тоом.
Rambler's Top100 Service
Поиск   
 
Обратите внимание!   Посмотрите новые поступления ... Обратите внимание!
 
  Наука >> Математика >> Алгебра, математическая логика и теория чисел | Книги
 Написать комментарий  Добавить новое сообщение
       
Next:   3 Показательная функция и формула Up:   Комплексные числа Previous:   1 Что такое комплексные

2 Модуль и аргумент комплексного числа

Повторить:п. 5.2: отбор чисел на круге.

В этом параграфе мы выясним геометрический смысл умножения комплексных чисел. Сначала - небольшая подготовка.

Рис. 112:
\begin{figure}\epsfbox{t29.1}\end{figure}

Расстояние на комплексной плоскости от начала координат (точки $ O$) до точки $ z$ называется модулем комплексного числа $ z$. Модуль комплексного числа $ z$ обозначается $ \vert z\vert$, как и модуль действительного числа. Такое совпадение обозначений не приводит к путанице, поскольку модуль действительного числа также равен расстоянию от соответствующей точки на числовой оси до точки $ O$. Если $ z = a + bi$, то, очевидно, $ \vert z\vert=\sqrt{a^2 +b^2}$ (рис. 112).

Задача 2.1   Докажите, что для любых комплексных чисел $ z$ и $ w$ верно неравенство $ \vert z+w\vert\leqslant \vert z\vert+ \vert w\vert$.

Теперь соединим точку $ z$ с точкой $ O$. Угол, образуемый полученным отрезком с действительной осью (точнее говоря, с положительным направлением действительной оси), называется аргументом числа $ z$ (рис. 113а). Этот угол принято выражать в радианах.

Рис. 113:
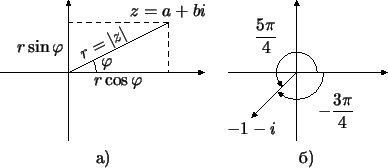
\begin{figure}\begin{tabular}{cc} \epsfbox{t29.2}& \epsfbox{t29.3}\\ а) & б) \end{tabular}\end{figure}

Если $ z = a + bi$, $ \vert z\vert= r$, аргумент $ z$ равен $ \varphi $, то, очевидно,

$\displaystyle a$ $\displaystyle = r\cos\varphi ;$    
$\displaystyle b$ $\displaystyle = r\sin\varphi .$    

Стало быть, $ z = r\cos\varphi + i r\sin\varphi = r(\cos\varphi + i\sin\varphi )$.

Запись комплексного числа в виде $ r(\cos\varphi + i\sin\varphi )$, где $ r>0$, называется тригонометрической формой комплексного числа. В тригонометрической форме можно записать любое комплексное число, кроме нуля (аргумент нуля мы не определяем).

Запишем, например, в тригонометрической форме число $ z = -1-i$. Очевидно, $ \vert z\vert=\sqrt 2$, и из рис. 113б видно, что в качестве аргумента можно взять $ 5\pi/4$:

$\displaystyle -1-i = 2\Bigr(\cos\frac{5\pi}4+ i\sin\frac{5\pi}4\Bigr). $

Впрочем, с тем же успехом можно было бы сказать, что аргумент $ -1-i$ равен $ -\frac{3\pi}4$: ведь равенство $ -1-i =\sqrt 2\Bigl(\cos\bigl(- \dfrac{3\pi}4\bigr) + i\sin\bigl(-\dfrac{3\pi}4\bigr)\Bigr)$ также верно. Вообще, аргумент комплексного числа определен не однозначно, а с точностью до прибавления $ 2\pi n$, где $ n$ - целое число. В качестве аргумента числа $ z$ можно взять любое число $ \varphi $, для которого $ z = \vert z\vert(\cos\varphi + i\sin\varphi )$.

Задача 2.2   Найдите аргументы следующих чисел, после чего запишите эти числа в тригонометрической форме: а) $ i$; б) $ -1$; в) $ \sqrt3 + i$; г) $ \sqrt3 - i$; д) $ -(\cos\varphi + i\sin\varphi )$; е) $ \cos\varphi - i\sin\varphi $.

Задача 2.3   Докажите, что

$\displaystyle \frac1{\cos\varphi +i\sin\varphi }=\cos\varphi -i\sin\varphi . $

Пусть теперь нам даны комплексные числа $ z_1= r_1(\cos\varphi _1+ i\sin\varphi _1)$ и  $ z_2= r_2(\cos\varphi _2 + i\sin\varphi _2)$. Давайте их перемножим:

$\displaystyle z_1z_2$ $\displaystyle =r_1(\cos\varphi _1+ i\sin\varphi _1)r_2(\cos\varphi _2 + i\sin\varphi _2)={}$    
$\displaystyle {}$ $\displaystyle =r_1r_2(\cos\varphi _1+ i\sin\varphi _1)(\cos\varphi _2 + i\sin\varphi _2)={}$    
$\displaystyle {}$ $\displaystyle =r_1r_2(\cos\varphi _1\cos\varphi _2- \sin\varphi _1\sin\varphi _2)+$    
  $\displaystyle \qquad{}+i(\sin\varphi _1\cos\varphi _2 +\cos\varphi _1\sin\varphi _2)={}$    
$\displaystyle {}$ $\displaystyle =r_1r_2(\cos(\varphi _1+\varphi _2) + i\sin(\varphi _1+\varphi _2)).$    

(мы воспользовались формулами синуса и косинуса суммы).

Как видите, если перейти к тригонометрической форме, то умножение комплексных чисел запишется простой формулой:

\begin{multline*} r_1(\cos\varphi _1+ i\sin\varphi _1)r_2(\cos\varphi _2 + i\si... ...r_2(\cos(\varphi _1+\varphi _2) + i\sin(\varphi _1+\varphi _2)). \end{multline*}

Или словами:

При умножении комплексных чисел их модули перемножаются, а аргументы складываются.

Поскольку деление - действие, обратное к умножению, то:

При делении комплексных чисел их модули делятся, а аргументы вычитаются.

Итак, мы придали геометрический смысл умножению комплексных чисел, рассматриваемых как векторы на плоскости. На первый взгляд это противоречит сказанному в п. 4.0, где мы говорили, что геометрически определить умножение векторов на плоскости невозможно. Представьте себе, однако, что у нас даны два вектора и мы хотим их умножить ``как комплексные числа'' - тут же выяснится, что для того, чтобы сложить аргументы, надо сначала иметь ось, от которой эти аргументы отсчитывать, причем если выбрать ``действительную ось'' по-другому, то произведение изменится!

Рассматривая умножение комплексных чисел, записанных в тригонометрической форме, мы убедились, что при умножении комплексных чисел их модули перемножаются. Запишем это свойство комплексных чисел в виде формулы

$\displaystyle \vert zw\vert =\vert z\vert\cdot \vert w\vert.$ (3)

Задача 2.4   Докажите формулу (3), исходя из определения умножения комплексных чисел.

Задача 2.5   а) Докажите, что $ \vert z\vert = z\cdot\bar z$; б) выведите из этой формулы тождество (3).

Формулу (3) можно переписать и не используя комплексных чисел. В самом деле, если $ z=a_1+b_1i$ и  $ w=a_2+b_2i$, то, возводя (3) в квадрат, получаем такое тождество:

$\displaystyle (a_1^2+b_1^2)(a_2^2+b_2^2)=(a_1a_2-b_1b_2)^2+ (a_1b_2+b_1a_2)^2.$ (4)

Разумеется, это тождество легко проверить и непосредственно.

Задача 2.6   Докажите, что число

$\displaystyle 32858969712941053630927296788431704044342041015625 = 5^{31}\cdot13^{25} $

является суммой квадратов двух целых чисел.

Задача 2.7   Докажите, что число

\begin{multline*} 73734314159378042035384049570 ={}\\ {}=2\cdot 5\cdot 13\cdot... ...89\cdot 97\cdot 101\cdot 113\cdot 137\cdot 149\cdot 157\cdot 173 \end{multline*}

также является суммой квадратов двух целых чисел.

Указание. $ 2=1^2+1^2$; $ 5=1^2+2^2$...

Существует аналог тождества (4) для сумм четырех квадратов, показывающий, что произведение двух сумм четырех квадратов также равно сумме четырех квадратов:

\begin{multline*} (a_1^2+a_2^2+a_3^2+a_4^2) (b_1^2+b_2^2+b_3^2+b_4^2)={}\\ {}=(... ...1b_3+a_3b_1-a_2b_4+a_4b_2)^2 + (a_1b_4+a_4b_1+a_2b_3-a_3b_2)^2. \end{multline*}

Задача 2.8   Докажите это тождество.

Имеется также аналог этих двух тождеств для сумм восьми квадратов, но на этом все и кончается: при $ n\ne 2, 4, 8$ тождеств типа ``произведение двух сумм $ n$ квадратов равно сумме $ n$ квадратов'' не существует.

Теперь посмотрим, что вытекает из того, что аргументы комплексных чисел при умножении складываются.

Если возвести комплексное число в степень $ n$, то есть умножить его на себя $ n$ раз, то его модуль возведется в степень $ n$, а аргумент умножится на $ n$:

$\displaystyle (r(\cos\varphi + i \sin\varphi ))^n= r^n(\cos n\varphi + i\sin n\varphi ). $

В частности, при $ r=1$ получится вот что:

$\displaystyle (\cos\varphi + i\sin\varphi )^n =\cos n\varphi + i\sin n\varphi . $

Эта формула называется формулой Муавра.

Из формулы Муавра легко вывести формулы, выражающие $ \cos n\varphi $ и $ \sin n\varphi $ через $ \cos\varphi $ и  $ \sin\varphi $. Для этого надо в ее левой части раскрыть скобки и привести подобные. При $ n = 5$, например, получится вот что:

$\displaystyle (\cos\varphi + i\sin\varphi )^5$ $\displaystyle = (\cos^5\varphi - 10\cos^3\varphi \sin^2\varphi + 5\cos\varphi \sin^4\varphi )+{}$    
  $\displaystyle {}+ i(5\cos^4\varphi \sin\varphi - 10\cos^2\varphi \sin^3\varphi +\sin^5\varphi )={}$    
$\displaystyle {}$ $\displaystyle =\cos 5\varphi + i\sin 5\varphi .$    

Так как выражения слева и справа равны, то равны по отдельности их вещественные и мнимые части, откуда:

$\displaystyle \cos 5\varphi$ $\displaystyle =\cos^5\varphi - 10\cos^3\varphi \sin^2\varphi + 5\cos\varphi \sin^4\varphi ,$    
$\displaystyle \sin 5\varphi$ $\displaystyle =5\cos^4\varphi \sin\varphi - 10cos^2\varphi \sin^3\varphi +\sin^5\varphi .$    

Чтобы получить такие формулы для произвольного $ n$, надо раскрывать скобки в  $ (\cos\varphi + i\sin\varphi )^n$, а для этого требуется общая формула для раскрытия скобок в выражении $ (a+b)^n$. Мы выпишем эту формулу, но не будем ее доказывать. Выглядит она так:

\begin{displaymath} \begin{array}{l} (a+b)^n=a^n + na^{n-1}b + \dfrac{n(n-1)}{1... ...dots2}{1\cdot 2\cdot \dots(n-1)} a^1b^{n-1} + b^n. \end{array}\end{displaymath}

Иными словами, в правой части коэффициент при $ a^{n-k}b^k$ равен $ \dfrac{n(n-1)\dots(n-k+1)}{1\cdot 2\cdot\dots\cdot k}$: в знаменателе стоит произведение первых $ k$ натуральных чисел, а в числителе - произведение $ k$ идущих подряд целых чисел в убывающем порядке, начиная с $ n$. Хотя коэффициенты в нашей формуле записаны как дроби, на самом деле все они - целые числа.

Формула для $ (a+b)^n$, которую мы выписали, называется формулой бинома Ньютона.

Задача 2.9   Проверьте формулу бинома Ньютона для $ n = 3,4,5$.

Задача 2.10   а) Выпишите формулу бинома Ньютона для $ n = 6$.

б) Выпишите формулы для $ \cos6\varphi $ и  $ \sin6\varphi $.

Задача 2.11   Убедитесь, что в формуле бинома Ньютона коэффициент при $ ab^{n-1}$ равен $ n$.

Задача 2.12   Докажите, что в формуле бинома Ньютона коэффициенты при $ a^{n-k}b^k$ и  $ a^kb^{n-k}$ равны (что и не удивительно: если левая часть тождества не меняется, когда меняешь местами $ a$ и $ b$, то такой же должна быть и правая часть).

Другое приложение формулы Муавра - еще один вывод формулы для суммы косинусов или синусов углов, образующих арифметическую прогрессию (п. 4.5). В самом деле, пусть нам надо вычислить сумму

$\displaystyle \cos\alpha +\cos(\alpha + \beta) +\cos(\alpha +2 \beta) +\ldots +\cos(\alpha +n \beta). $

Рассмотрим комплексные числа $ a =\cos\alpha+ i\sin\alpha$, $ b =\cos\beta + i\sin\beta$. Тогда, очевидно, $ ab^k =\cos(\alpha+k\beta) + i\sin(\alpha+k\beta)$. Следовательно,

\begin{displaymath} \begin{array}{@{}l@{}} a+ab+ab^2 +\ldots+ab^n= (\cos + \cos... ...\sin(\alpha + \beta)+\ldots+\sin(\alpha +n \beta)). \end{array}\end{displaymath}

Однако правую часть можно вычислить по формуле для суммы геометрической прогрессии:

\begin{displaymath} \begin{array}{@{}l@{}} a+ab+ab^2 +\ldots+ab^n=a\dfrac{1-b^{... ...\beta-i \sin(n+1)\beta}{1-\cos\alpha- i\sin\alpha}. \end{array}\end{displaymath}

(Если вас смущает, что мы применяем эту формулу к комплексным числам, посмотрите в вашем школьном учебнике, как она доказывается, и убедитесь, что дословно то же доказательство годится и для комплексных чисел.)

Теперь осталось упростить выражение в правой части (для этого, как обычно при делении комплексных чисел, надо умножить числитель и знаменатель дроби на $ (1-\cos\alpha)+i \sin\alpha$ и выделить в полученном выражении действительную и мнимую части. Действительная часть будет равна $ \cos\alpha + \cos(\alpha +\beta)+\ldots+\cos(\alpha +n\beta)$, а мнимая часть будет равна $ \sin\alpha + \sin(\alpha+\beta)+\ldots+\sin(\alpha +n\beta)$.

Задача 2.13   Проведите эти выкладки и убедитесь, что ответы совпадают с полученными в п. 4.5.

Раз с помощью тригонометрической формы комплексные числа удобно возводить в степень, естественно надеяться, что та же тригонометрическая форма поможет и в выполнении обратной операции - извлечения корней из комплексных чисел. Покажем на примере, какие новые явления при этом возникают.

Давайте извлечем корень пятой степени из 32, то есть найдем число, которое, будучи возведенным в пятую степень, даст 32. Среди действительных чисел такое число одно - это число 2. Посмотрим, что будет, если рассматривать любые комплексные числа. Мы ищем такие числа $ z$, что $ z^5= 32$. Проще всего найти модуль числа $ z$: если $ z^5= 32$, то $ \vert z^5\vert=\vert z\vert^5= 32$ (при перемножении чисел модули перемножаются), откуда $ z= 2$ (уж $ \vert z\vert$-то - это обычное действительное число, так что тут никаких разночтений не будет). Осталось найти аргумент $ z$. Для этого запишем $ z$ в тригонометрической форме: $ z = 2(\cos\varphi + i \sin\varphi )$. Тогда $ z^5= 32(\cos 5\varphi + i \sin 5\varphi )$, откуда $ 32(\cos 5\varphi + i \sin 5\varphi ) = 32$, $ \cos 5\varphi + i \sin 5\varphi = 1$, что, в свою очередь, равносильно системе тригонометрических уравнений

$\displaystyle \left\{ \begin{aligned} \cos 5\varphi &= 1;\\ \sin 5\varphi &=0. \end{aligned}\right. $

Этой системе, очевидно, удовлетворяют в точности те и только те числа $ \varphi $, для которых числу $ 5\varphi $ соответствует начало отсчета на тригонометрической окружности, то есть $ 5\varphi = 2 k\pi$, или $ \varphi =2\pi k/5$ ( $ k\in\mathbb{Z})$. Стало быть, решения уравнения $ z^5= 32$ - это числа вида $ 2(\cos2\pi k/5 + i \sin2\pi k/5)$, где $ k\in \mathbb{Z}$. Не все эти числа различны: так как комплексные числа с аргументами, отличающимися на $ 2\pi$, совпадают, то разные комплексные числа получаются только при $ k = 0,1,2,3,4$, а дальше значения $ z$ будут повторяться. Итак, все корни уравнения $ z^5= 32$ или, если угодно, все корни пятой степени из 32 таковы:

$\displaystyle z_1$ $\displaystyle = 2(\cos 0 + i \sin 0);$    
$\displaystyle z_2$ $\displaystyle = 2(\cos 2\pi/5+ i \sin2\pi/5);$    
$\displaystyle z_3$ $\displaystyle = 2(\cos 4\pi/5+ i \sin4\pi/5);$    
$\displaystyle z_4$ $\displaystyle = 2(\cos 6\pi/5+ i \sin6\pi/5);$    
$\displaystyle z_5$ $\displaystyle = 2(\cos 8\pi/5+ i \sin8\pi/5);$    

Здесь $ z_1$ - это просто число 2, действительный корень уравнения $ z^5= 32$. Прочие корни этого уравнения действительными

Рис. 114:
\begin{figure}\epsfbox{t29.4}\end{figure}

уже не являются. Если изобразить все корни пятой степени из 32 на комплексной плоскости, то окажется, что они расположены в вершинах правильного пятиугольника.

В наших рассуждениях не играло никакой роли ни то, что мы извлекали корень именно степени 5, ни то, что мы извлекали его из 32. На самом деле для всякого комплексного числа $ a\ne0$ существует ровно $ n$ решений уравнения $ z^n= a$ (эти решения называются корнями степени $ n$ из $ a$). При изображении на комплексной плоскости корни степени $ n$ из $ a$ располагаются в вершинах правильного $ n$-угольника с центром в точке 0.

Задача 2.14   Найдите: а) все три кубических корня из $ i$; б) все шесть корней степени 6 из 1 и изобразите их на комплексной плоскости.

Задача 2.15   а) Докажите, что произведение двух корней степени $ n$ из 1 - тоже корень степени $ n$ из 1.

б*) Пусть $ z_1,z_2,\dots,z_n$ - все корни степени $ n$ из 1, $ k$ - целое число. Докажите, что

$\displaystyle z_1^k+z_2^k+\dots+z_n^k= \begin{cases} 0, &\text{если $k$ не дели... ...лексные числа!извлечение корней\vert)}\index{Корни из комплексных чисел\vert)} $

Мы добавили к обычным вещественным числам число $ i$ для того, чтобы можно было извлекать квадратные корни из отрицательных чисел; при этом оказалось, что в комплексных числах можно решить любое квадратное уравнение. Замечательно, что и вообще любое алгебраическое уравнение имеет корень в комплексных числах: никаких новых чисел помимо $ i$ ради этого вводить не надо. Этот важный факт, который называют по традиции основной теоремой алгебры, доказал в конце 18 века великий немецкий математик К.Ф.Гаусс.

       


Написать комментарий
 Copyright © 2000-2015, РОО "Мир Науки и Культуры". ISSN 1684-9876 Rambler's Top100 Яндекс цитирования