Next: 3 Как решать тригонометрические
Up: Тригонометрия для абитуриентов
Previous: 1 Как решать тригонометрические
Subsections
Повторить:п. 2. Определение тригонометрических функций.
п. 2.6. Простейшие тригонометрические уравнения.
В уравнениях, встречавшихся нам до сих пор, при отборе корней
получалось так, что при проверке в ответ включалась или же
отбрасывалась вся серия целиком. В этом параграфе мы расскажем,
что делать в более сложных случаях, когда часть серии в ответ
входит, а часть - нет.
Пример 2.1
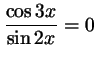 . .
Решение. Это уравнение, очевидно, равносильно системе
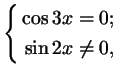 или
или
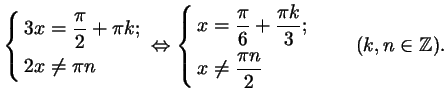 Итак, нам нужно из множества всех
Итак, нам нужно из множества всех  , представимых в виде , представимых в виде
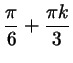 , где , где  - некоторое целое число,
выкинуть посторонние корни - те, что представимы в виде - некоторое целое число,
выкинуть посторонние корни - те, что представимы в виде
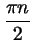 , где , где 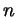 - какое-то целое число. Для этого
нанесем на тригонометрический круг все числа вида - какое-то целое число. Для этого
нанесем на тригонометрический круг все числа вида
 , где , где
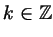 (рис. 102а). (рис. 102а).
Рис. 102:
 |
При этом получится 6 точек, обозначенных на рис. 102а. Эти
точки появляются, если взять любые 6 последовательных значений
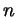 , при остальных , при остальных 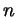 точки будут повторяться. Более того, ясно,
что всякое число, которому соответствует одна из отмеченных на
рис. 102а точек, имеет вид точки будут повторяться. Более того, ясно,
что всякое число, которому соответствует одна из отмеченных на
рис. 102а точек, имеет вид
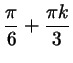 для некоторого целого
для некоторого целого  . .
Если нанести на этот рисунок еще и точки, соответствующие числам
вида
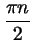 , то у нас получится рис. 102б
(точки, соответствующие числам , то у нас получится рис. 102б
(точки, соответствующие числам
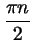 , отмечены белыми
кружками). Ответом к нашему уравнению будут числа, представимые в
виде , отмечены белыми
кружками). Ответом к нашему уравнению будут числа, представимые в
виде
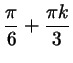 и при этом не представимые в виде и при этом не представимые в виде
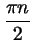 . Иными словами, решения
уравнения - числа, которым соответствуют черные кружки, не
совпадающие с белыми. Обращаясь к рис. 102б, видим, что
таких кружков ровно четыре, и каждому из них
соответствует бесконечная серия значений . Иными словами, решения
уравнения - числа, которым соответствуют черные кружки, не
совпадающие с белыми. Обращаясь к рис. 102б, видим, что
таких кружков ровно четыре, и каждому из них
соответствует бесконечная серия значений  : :
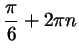 ; ;
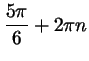 ; ;
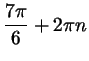 ; ;
 . Можно также объединить первую серию
с третьей, а вторую - с четвертой. Тогда
ответ запишется так: . Можно также объединить первую серию
с третьей, а вторую - с четвертой. Тогда
ответ запишется так:
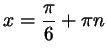 ; ;
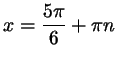 ( (
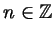 ). ).
Мы не случайно при записи системы
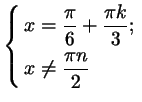 использовали две разные буквы для
обозначения ``произвольного целого числа'': ведь если
использовали две разные буквы для
обозначения ``произвольного целого числа'': ведь если
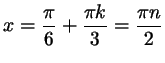 , где , где 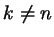 , то , то
 - все равно посторонний корень. Например, так будет при - все равно посторонний корень. Например, так будет при 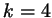 и и 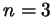 (получается посторонний корень (получается посторонний корень 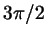 ). ).
Пример 2.2
 . .
Решение Это уравнение равносильно системе
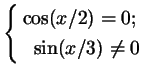 или или 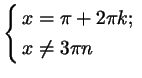 ($k,n&isin#in; ($k,n&isin#in;
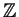 $). $). Попробуем
действовать так же, как и в предыдущем примере: нанесем на
тригонометрический круг черные точки - числа вида
Попробуем
действовать так же, как и в предыдущем примере: нанесем на
тригонометрический круг черные точки - числа вида
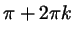 и белые точки - числа вида и белые точки - числа вида 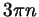 . То, что получится,
изображено на рис. 103. . То, что получится,
изображено на рис. 103.
Рис. 103:
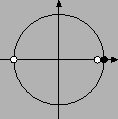 |
На основании этого рисунка надо, казалось бы, сделать вывод, что
решений у уравнения нет: ведь на рисунке нет черных точек, не
совпадающих с белыми. Тем не менее легко видеть, что, скажем,
число 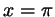 будет решением уравнения. Где же мы ошиблись? Дело
в том, что изображение чисел вида будет решением уравнения. Где же мы ошиблись? Дело
в том, что изображение чисел вида 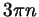 , где , где
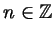 , на
тригонометрическом круге неадекватно: верно, что все такие числа
изображаются одной из белых точек на рис. 103, но
неверно, что все числа, соответствующие белым точкам, имеют вид , на
тригонометрическом круге неадекватно: верно, что все такие числа
изображаются одной из белых точек на рис. 103, но
неверно, что все числа, соответствующие белым точкам, имеют вид
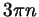 с целым с целым 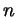 : белым точкам на рис. 103
соответствуют и числа : белым точкам на рис. 103
соответствуют и числа 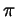 , , 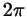 , , 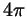 , , 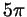 и т.д. и т.д.
Вообще, изображение множества чисел на тригонометрическом круге
будет адекватно, только если это множество ``имеет период
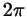 '': вместе с каждым числом '': вместе с каждым числом  содержит числа содержит числа 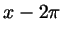 и и
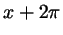 . В частности, будет иметь период . В частности, будет иметь период 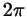 множество
решений уравнения, обе части которого имеют период множество
решений уравнения, обе части которого имеют период 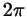 как
функции от как
функции от  . .
Доведем теперь до конца решение уравнения
 . Все, что нам нужно, - выяснить, для
каких целых чисел . Все, что нам нужно, - выяснить, для
каких целых чисел  число число
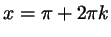 окажется
посторонним корнем. Это будет тогда, когда найдется такое число окажется
посторонним корнем. Это будет тогда, когда найдется такое число
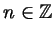 , что , что
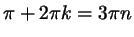 . Сокращая в этом равенстве
на . Сокращая в этом равенстве
на 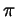 , получаем вопрос, к которому все сводится:
для каких , получаем вопрос, к которому все сводится:
для каких
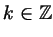 существует такое существует такое
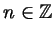 , что , что
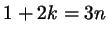 ? ?
Чтобы ответить на этот вопрос, выразим  через через 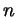 : :
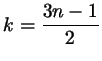 ;
выделим из этой дроби ``целую часть'': ;
выделим из этой дроби ``целую часть'':
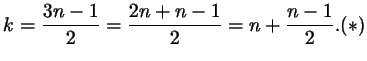 Так как
Так как  и и 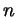 - целые числа, то - целые числа, то
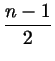 - тоже
целое число. Значит, - тоже
целое число. Значит,
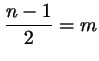 , ,
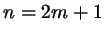 ( (
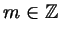 ).
Подставляя в ).
Подставляя в 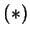 , получаем , получаем
 ( (
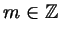 ). Итак, мы
получили ответ на наш вопрос: посторонние корни получаются при ). Итак, мы
получили ответ на наш вопрос: посторонние корни получаются при
 , ,
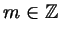 . Нас же интересуют как раз все остальные . Нас же интересуют как раз все остальные
 . Ясно, что сказать `` . Ясно, что сказать ``
 , ,
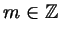 '' - все
равно, что сказать ``число '' - все
равно, что сказать ``число  при делении на при делении на  дает остаток,
не равный дает остаток,
не равный 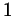 ''. Однако кроме единицы при делении на ''. Однако кроме единицы при делении на  возможны только остатки 0 или
возможны только остатки 0 или 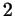 . Так что можно еще сказать,
что для числа . Так что можно еще сказать,
что для числа
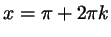 , являющегося корнем, число , являющегося корнем, число  дает при делении на
дает при делении на  остаток 0 или остаток 0 или 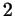 , или, иными словами, , или, иными словами,
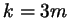 или или
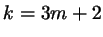 , ,
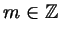 . Подставляя это выражение
для . Подставляя это выражение
для  , получаем окончательно ответ: , получаем окончательно ответ:
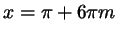 или или
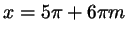 . .
Прием, позволивший нам выделить ``плохие'' значения  ,
срабатывает всегда; как им пользоваться в общем случае,
рассказано в приложении к этому параграфу. ,
срабатывает всегда; как им пользоваться в общем случае,
рассказано в приложении к этому параграфу.
Заметим еще, что и для уравнения
 можно было бы обойтись изображением чисел на круге. Для
этого надо было бы сделать замену переменной можно было бы обойтись изображением чисел на круге. Для
этого надо было бы сделать замену переменной 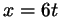 . После
этого уравнение принимает вид . После
этого уравнение принимает вид
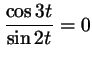 . Левая
часть этого уравнения уже имеет период . Левая
часть этого уравнения уже имеет период 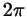 как функция от как функция от 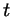 ,
так что его можно решать, отбирая числа на круге. Найдя ,
так что его можно решать, отбирая числа на круге. Найдя 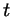 ,
остается найти ,
остается найти 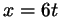 . .
Задача 2.1
Решите уравнения:
а)
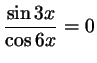 ;
б) ;
б)
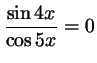 ;
в) ;
в)
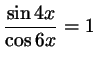 ;
г) ;
г)
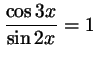 ;
д) ;
д)
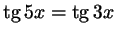 . .
Задача 2.2
Решите уравнения:
а)
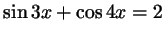 ;
б) ;
б)
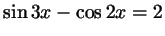 ;
в) ;
в)
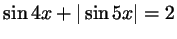 ;
г) ;
г)
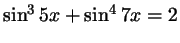 ;
д) ;
д)
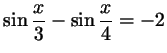 . .
Указание к пункту а). При всех  верны неравенства верны неравенства
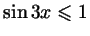 , ,
 . Складывая их, получаем,
что . Складывая их, получаем,
что
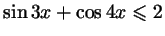 , причем равенство достигается
только в том случае, когда оба слагаемых одновременно равны , причем равенство достигается
только в том случае, когда оба слагаемых одновременно равны 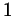 . .
Задача 2.3
Решите уравнения:
а)
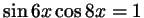 ;
б) ;
б)
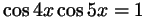 ;
в) ;
в)
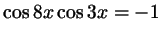 ;
г) ;
г)
 ;
д) ;
д)
 . .
Указание к пункту а). При всех  верны
неравенства верны
неравенства
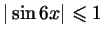 , ,
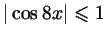 . Следовательно, . Следовательно,
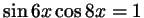 тогда и только тогда, когда оба сомножителя
одновременно равны тогда и только тогда, когда оба сомножителя
одновременно равны 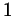 или или 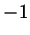 . .
Задача 2.4
а) Решите уравнение
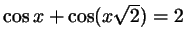 . .
б) При каких
значениях 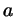 уравнение уравнение
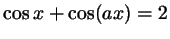 имеет бесконечно
много решений? имеет бесконечно
много решений?
При отборе корней
тригонометрических уравнений иногда приходится отвечать на
вопросы наподобие: ``для каких
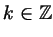 существует такое существует такое
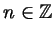 , что , что
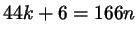 ''? Посмотрим на этот вопрос
немного с другой стороны: выясним, для каких вообще целых ''? Посмотрим на этот вопрос
немного с другой стороны: выясним, для каких вообще целых  и и
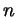 выполняется равенство выполняется равенство
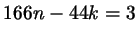 . Такого рода задачи
называются неопределенными
уравнениями (точнее говоря, линейными неопределенными
уравнениями с двумя неизвестными, но эти уточняющие слова мы
будем опускать, поскольку других неопределенных уравнений нам не
встретится). Расскажем, как можно
решать такие уравнения. . Такого рода задачи
называются неопределенными
уравнениями (точнее говоря, линейными неопределенными
уравнениями с двумя неизвестными, но эти уточняющие слова мы
будем опускать, поскольку других неопределенных уравнений нам не
встретится). Расскажем, как можно
решать такие уравнения.
Первое, что надо сделать для решения неопределенного уравнения,
- это найти наибольший общий
делитель коэффициентов при неизвестных и попробовать сократить
на него обе части уравнения (разумеется, свободный член должен
при этом остаться целым числом). Рассмотрим, например, уравнение
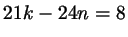 . Наибольший общий делитель коэффициентов равен
3, и сократить на него не удается, так как . Наибольший общий делитель коэффициентов равен
3, и сократить на него не удается, так как 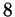 на на  не
делится. Тогда можно сразу сказать, что это уравнение решений
в целых числах не имеет. В самом деле, если не
делится. Тогда можно сразу сказать, что это уравнение решений
в целых числах не имеет. В самом деле, если 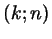 - решение
этого уравнения 13, то левая часть делится
на - решение
этого уравнения 13, то левая часть делится
на  (так как на (так как на  делятся оба коэффициента), а правая часть
на делятся оба коэффициента), а правая часть
на  не делится. Значит, у этого уравнения решений
нет. Сформулируем примененное нами соображение в общем виде: не делится. Значит, у этого уравнения решений
нет. Сформулируем примененное нами соображение в общем виде:
Если в уравнении
 (с целыми (с целыми 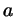 , , 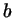 и и 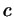 )
коэффициенты )
коэффициенты 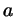 и и 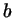 делятся на некоторое число делятся на некоторое число 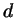 , а
свободный член , а
свободный член 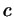 не делится на не делится на 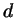 , то это уравнение не имеет
решений в целых числах. , то это уравнение не имеет
решений в целых числах.
Мы указали одну причину, по которой наше неопределенное уравнение
может не иметь решений. Оказывается, во всех остальных случаях
решения обязательно будут.
Если в неопределенном уравнении
 свободный член свободный член 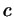 делится на наибольший общий делитель коэффициентов
делится на наибольший общий делитель коэффициентов 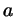 и и 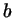 (в
частности, так будет, если (в
частности, так будет, если 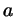 и и 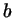 вообще не имеют общих
делителей, кроме единицы), то уравнение обязательно имеет решения
в целых числах. вообще не имеют общих
делителей, кроме единицы), то уравнение обязательно имеет решения
в целых числах.
Мы не будем доказывать это утверждение, а просто покажем, как
искать решения.
Решим уравнение
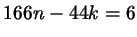 . Для начала, как мы уже
говорили, поделим обе части на . Для начала, как мы уже
говорили, поделим обе части на 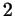 : :
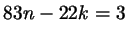 . Теперь
выберем ту неизвестную, коэффициент при которой меньше по
абсолютной величине - в нашем случае это . Теперь
выберем ту неизвестную, коэффициент при которой меньше по
абсолютной величине - в нашем случае это  , - и выразим ее
через другую неизвестную: , - и выразим ее
через другую неизвестную:
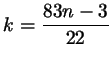 . Выделим в этой
дроби целую часть: . Выделим в этой
дроби целую часть:
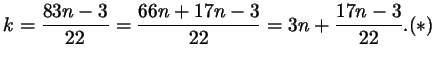 Как видите, целочисленные решения нашего уравнения будут
получаться, если подставлять в него все те целые
Как видите, целочисленные решения нашего уравнения будут
получаться, если подставлять в него все те целые 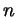 , для которых
число , для которых
число
 тоже будет целым: ведь тогда из тоже будет целым: ведь тогда из  получается, что и
получается, что и  - целое число. Но как же узнать, когда
число - целое число. Но как же узнать, когда
число
 будет целым? Для этого обозначим будет целым? Для этого обозначим
 буквой буквой 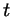 и запишем: и запишем:
 , или , или
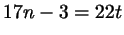 . Как видите, снова получилось
неопределенное уравнение, но его коэффициенты уже меньше, чем у
исходного. Проделаем с этим новым уравнением ту же операцию, что
и c исходным: выразим из него ту неизвестную, коэффициент при которой
меньше по абсолютной величине (на сей раз это будет . Как видите, снова получилось
неопределенное уравнение, но его коэффициенты уже меньше, чем у
исходного. Проделаем с этим новым уравнением ту же операцию, что
и c исходным: выразим из него ту неизвестную, коэффициент при которой
меньше по абсолютной величине (на сей раз это будет 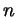 ), и
выделим из получающейся дроби целую часть: ), и
выделим из получающейся дроби целую часть:
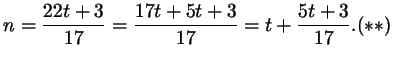 Из
Из  видно, что число видно, что число
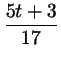 обязано быть
целым. Обозначим его буквой обязано быть
целым. Обозначим его буквой 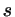 : :
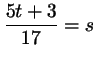 , ,
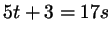 . Продолжая в том же духе, выразим . Продолжая в том же духе, выразим 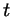 через через 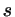 : :
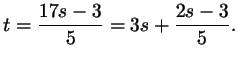 Обозначим, далее,
Обозначим, далее,
 буквой буквой 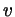 : :
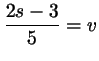 , ,
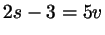 , ,
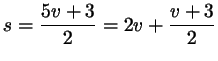 .
Обозначим, наконец, .
Обозначим, наконец,
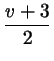 буквой буквой 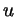 : :
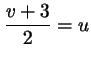 , ,
 . В этом месте наши мучения и кончаются. В самом
деле, нам надо выяснить, для каких целых . В этом месте наши мучения и кончаются. В самом
деле, нам надо выяснить, для каких целых 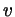 число число
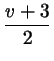 будет целым, и ответ на этот вопрос уже готов: если
будет целым, и ответ на этот вопрос уже готов: если
 ,
где ,
где 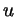 - любое целое число! (дело тут, конечно, в том, что в
неопределенном уравнении - любое целое число! (дело тут, конечно, в том, что в
неопределенном уравнении
 коэффициент при коэффициент при 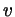 равен
единице). Теперь, чтобы получить решения исходного уравнения, нам
осталось последовательно выразить равен
единице). Теперь, чтобы получить решения исходного уравнения, нам
осталось последовательно выразить 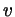 через через 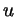 , , 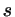 через через 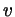 , ,
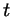 через через 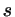 , , 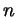 через через 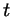 и и  через через 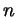 . Отправимся в
обратный путь: . Отправимся в
обратный путь:
 ; ;
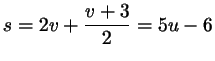 ; ;
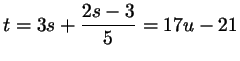 ; ;
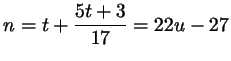 ; ;
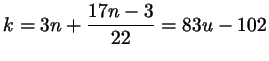 . Итак, решение получено: . Итак, решение получено:
 , ,
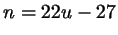 , где , где 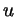 - произвольное целое число.
Стало быть, ответ на наш исходный вопрос таков: пусть - произвольное целое число.
Стало быть, ответ на наш исходный вопрос таков: пусть  -
целое число. Тогда -
целое число. Тогда
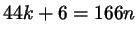 для некоторого для некоторого
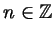 тогда и
только тогда, когда тогда и
только тогда, когда
 , где , где
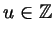 . .
Изложенный нами способ нахождения решения линейного
неопределенного уравнения с целыми коэффициентами называется
алгоритмом Евклида.
Задача 2.5
Для каких целых  существует такое целое существует такое целое 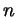 , что , что
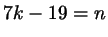 ? ?
Задача 2.6
Решите уравнения в целых числах:
а)
 ;
б) ;
б)
 ;
в*
) ;
в*
)
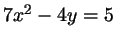 . .
Задача 2.7
При решении в целых числах уравнения
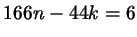 нам
пришлось ввести помимо нам
пришлось ввести помимо 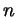 и и  четыре дополнительные
переменные ( четыре дополнительные
переменные (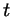 , , 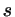 , , 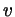 и и 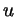 ). Приведите пример
неопределенного уравнения вида ). Приведите пример
неопределенного уравнения вида  , в котором , в котором 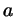 и и 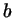 -
двузначные числа, для решения которого по изложенному методу надо
ввести шесть дополнительных переменных. Попробуйте также
доказать, что большего количества дополнительных переменных при
двузначных -
двузначные числа, для решения которого по изложенному методу надо
ввести шесть дополнительных переменных. Попробуйте также
доказать, что большего количества дополнительных переменных при
двузначных 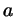 и и 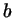 никогда не
потребуется. никогда не
потребуется.
Написать комментарий
|

