Next: 3 Простейшие формулы
Up: Начальные свойства тригонометрических функций
Previous: 1 Часы, или современный
Subsections
В этом параграфе мы аккуратно сформулируем определения
тригонометрических функций.
Для этого введем на плоскости прямоугольную систему координат
и рассмотрим окружность радиуса 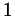 с центром в начале координат
(рис. 24а). с центром в начале координат
(рис. 24а).
Рис. 24:
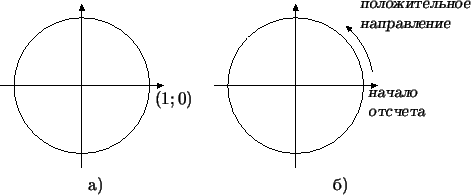 |
Такой чертеж принято называть
тригонометрическим
кругом (или тригонометрической окружностью). Точку
с координатами 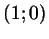 , лежащую на этой окружности, будем
называть началом отсчета или точкой ноль (не
путайте с началом координат!). Направление движения против
часовой стрелки будем называть положительным направлением
(рис. 24б). , лежащую на этой окружности, будем
называть началом отсчета или точкой ноль (не
путайте с началом координат!). Направление движения против
часовой стрелки будем называть положительным направлением
(рис. 24б).
Тригонометрическая окружность служит для того, чтобы
наносить на нее числа. Это делается так. Пусть у нас есть
число  . Начав с начала отсчета, пройдем по тригонометрической
окружности путь длиной . Начав с начала отсчета, пройдем по тригонометрической
окружности путь длиной 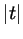 : если : если 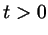 - в положительном
направлении, если - в положительном
направлении, если 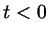 - в отрицательном (возможно, нам
придется при этом несколько раз пройти по одному и тому же
месту). Точка, в которой мы остановились, и есть точка на
окружности, соответствующая числу - в отрицательном (возможно, нам
придется при этом несколько раз пройти по одному и тому же
месту). Точка, в которой мы остановились, и есть точка на
окружности, соответствующая числу  . .
По-другому точку на окружности, соответствующую числу  , можно
себе представить как второй конец намотанной на окружность
нерастяжимой нити длины , можно
себе представить как второй конец намотанной на окружность
нерастяжимой нити длины 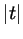 , один конец которой закреплен
в начале отсчета, или как положение стрелки часов, о которых мы
говорили в предыдущем параграфе, в момент , один конец которой закреплен
в начале отсчета, или как положение стрелки часов, о которых мы
говорили в предыдущем параграфе, в момент  . .
Рис. 25:
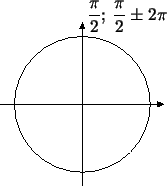 |
На рис. 25 отмечено, какая точка соответствует
числу
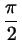 (длина дуги от 0 до этой точки составляет как раз (длина дуги от 0 до этой точки составляет как раз
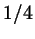 всей длины окружности, т.е. всей длины окружности, т.е.
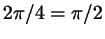 ). Впрочем, в ту
же точку попадут и числа ). Впрочем, в ту
же точку попадут и числа
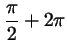 , ,
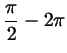 , ,
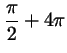 - при движении по окружности мы сделаем один или
несколько лишних кругов, но остановимся все в той же точке. - при движении по окружности мы сделаем один или
несколько лишних кругов, но остановимся все в той же точке.
Задача 2.1
Нанесите на тригонометрический круг числа 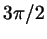 , , 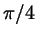 , ,
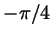 , , 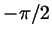 , , 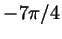 , , 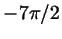 . Сколько различных точек
у вас получилось? . Сколько различных точек
у вас получилось?
Задача 2.2
Нанесите на тригонометрическую окружность точки,
соответствующие числам 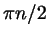 для всех целых для всех целых 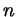 . Сколько
различных точек у вас получилось? . Сколько
различных точек у вас получилось?
Задача 2.3
Выполните задание предыдущей задачи для чисел:
а)
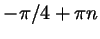 ;
б) ;
б)
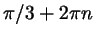 ( (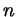 - любое целое число). - любое целое число).
Задача 2.4
В какой четверти будет находиться точка тригонометрической
окружности, соответствующая числу 1000?
Задача 2.5
Сколько точек получится, если нанести на тригонометрический круг
все числа вида
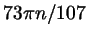 , где , где 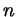 - целое число? - целое число?
Задача 2.6
Каким должно быть число  , чтобы среди точек, соответствующих
числам вида , чтобы среди точек, соответствующих
числам вида 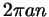 при всех целых при всех целых 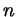 , было бы конечное число
различных? , было бы конечное число
различных?
Задача 2.7
Пусть числу  соответствует на тригонометрической окружности
точка соответствует на тригонометрической окружности
точка 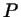 . Запишите какое-нибудь другое число, которому на
тригонометрической окружности соответствуют:
а)
та же самая точка . Запишите какое-нибудь другое число, которому на
тригонометрической окружности соответствуют:
а)
та же самая точка 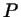 ;
б)
точка, симметричная точке ;
б)
точка, симметричная точке 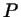 относительно начала координат;
в)
точка, симметричная точке относительно начала координат;
в)
точка, симметричная точке 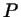 относительно оси абсцисс;
г)
точка, симметричная точке относительно оси абсцисс;
г)
точка, симметричная точке 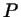 относительно оси ординат;
д)
точка, симметричная точке относительно оси ординат;
д)
точка, симметричная точке 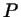 относительно
биссектрисы первого и третьего координатных углов. относительно
биссектрисы первого и третьего координатных углов.
Задача 2.8
Как выглядит на тригонометрическом круге множество точек,
соответствующих числам из промежутков:
а) ![$ [0;\pi/2]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img106.gif) ; б) ; б)
![$ [\pi/2;2\pi]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img107.gif) ; в) ; в)
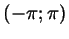 ; г) ; г) 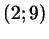 . .
Рис. 26
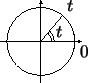 |
Если 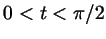 , то число , то число  на круге будет расположено так,
что отрезок, соединяющий соответствующую точку с началом
координат, составит угол на круге будет расположено так,
что отрезок, соединяющий соответствующую точку с началом
координат, составит угол  радиан с осью
абсцисс. В самом деле, в этом случае длина дуги от 0 до радиан с осью
абсцисс. В самом деле, в этом случае длина дуги от 0 до  будет
как раз равна будет
как раз равна  (рис. 26).
(рис. 26).
Теперь все готово для того, чтобы ввести основные
определения тригонометрии.
Определение. Косинусом числа
 называется абсцисса точки на
тригонометрическом круге, соответствующей числу называется абсцисса точки на
тригонометрическом круге, соответствующей числу  . .
Если  - радианная мера острого угла, то косинус этого угла
в нашем прежнем смысле равен косинусу числа - радианная мера острого угла, то косинус этого угла
в нашем прежнем смысле равен косинусу числа  в новом смысле. в новом смысле.
Косинус числа  обозначается обозначается 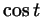 . .
Определение. Синусом числа
 называется ордината точки на
тригонометрическом круге, соответствующей числу называется ордината точки на
тригонометрическом круге, соответствующей числу  . .
Если  - радианная мера острого угла, то синус этого угла
в нашем прежнем смысле равен синусу числа - радианная мера острого угла, то синус этого угла
в нашем прежнем смысле равен синусу числа  в новом смысле. в новом смысле.
Синус числа  обозначается обозначается 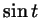 . .
Определение. Тангенсом числа
 называется отношение синуса
числа называется отношение синуса
числа  к его косинусу. к его косинусу.
Если  - радианная мера острого угла, то тангенс этого угла
в нашем прежнем смысле равен тангенсу числа - радианная мера острого угла, то тангенс этого угла
в нашем прежнем смысле равен тангенсу числа  в новом смысле
(так как для острых углов верна формула в новом смысле
(так как для острых углов верна формула
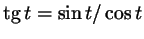 ). ).
Тангенс числа  обозначается обозначается
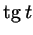 . .
Определения синуса и косинуса, которые вы сейчас прочитали, -
это те же самые определения, что были даны в предыдущем параграфе,
только сформулированные более аккуратно. В предыдущем же
параграфе было объяснено, почему для острых углов эти определения
согласуются с прежними.
Кроме синуса, косинуса и тангенса используются также и менее
употребительные функции
котангенс,
секанс
и косеканс, которые
определяются так:
Теперь, когда мы определили тригонометрические функции числового
аргумента, можно узнать, чему равны тригонометрические функции не
только острых, но и прямого и тупых углов: надо перевести
величину угла в радианы и взять синус, косинус или тангенс от
получившегося числа.
Задача 2.9
Заполните пустые места в следующей таблице:
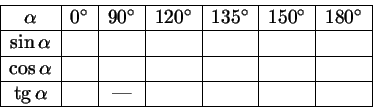
Замечание. В графе для
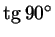 мы сразу поставили
прочерк, так как, по определению, мы сразу поставили
прочерк, так как, по определению,
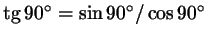 , но , но
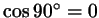 , так что , так что
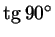 не определен. не определен.
Задача 2.10
Определите котангенс, секанс и косеканс острых углов с помощью
прямоугольных треугольников (аналогично тому, как мы определяли
синус, косинус и тангенс).
Задача 2.11
Одна из вершин правильного шестиугольника, вписанного
в тригонометрическую окружность, расположена в начале
отсчета. Найдите координаты остальных его вершин.
Задача 2.12
Тот же вопрос, что и в предыдущей задаче, но для правильного
пятиугольника (указание: см. задачу 13).
Задача 2.13
В задаче 23 было сказано, что в качестве
приближенного значения косинуса малого угла 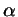 можно взять
число можно взять
число 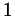 , то есть значение функции косинус в нуле. Что, если
в качестве приближенного значения для синуса малого
угла , то есть значение функции косинус в нуле. Что, если
в качестве приближенного значения для синуса малого
угла 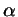 , не мудрствуя лукаво, взять , не мудрствуя лукаво, взять 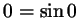 ? Чем это
плохо? ? Чем это
плохо?
Рис. 27:
Точка 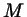 движется по циклоиде. движется по циклоиде.
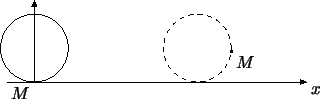 |
Задача 2.14
Рассмотрим колесо радиуса 1, касающееся оси абсцисс в начале
координат (рис. 27). Предположим, что колесо
покатилось по оси абсцисс в положительном направлении со скоростью
1 (т.е. за время  его центр смещается на его центр смещается на  вправо). вправо).
а)
Нарисуйте (примерно) кривую, которую
будет описывать точка 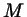 , касающаяся в первый момент оси
абсцисс.
б)
Найдите, каковы будут абсцисса и ордината точки , касающаяся в первый момент оси
абсцисс.
б)
Найдите, каковы будут абсцисса и ордината точки 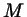 через
время через
время  после начала движения. после начала движения.
Синус и косинус мы в этом параграфе определили геометрически, как
ординату и абсциссу точки, а тангенс - алгебраически, как
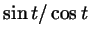 . Можно, однако, и тангенсу придать геометрический
смысл. . Можно, однако, и тангенсу придать геометрический
смысл.
Для этого проведем через точку с координатами 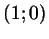 (начало
отсчета на тригонометрической окружности) касательную
к тригонометрической окружности - прямую, параллельную оси
ординат. Назовем эту прямую осью тангенсов
(рис. 28). Название это оправдывается так: пусть (начало
отсчета на тригонометрической окружности) касательную
к тригонометрической окружности - прямую, параллельную оси
ординат. Назовем эту прямую осью тангенсов
(рис. 28). Название это оправдывается так: пусть 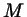 - точка на тригонометрической окружности, соответствующая числу
- точка на тригонометрической окружности, соответствующая числу
 . Продолжим радиус . Продолжим радиус 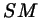 до пересечения с осью
тангенсов. Тогда оказывается, что ордината точки пересечения
равна до пересечения с осью
тангенсов. Тогда оказывается, что ордината точки пересечения
равна
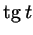 . .
В самом деле, треугольники 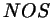 и и 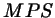 на рис. 28,
очевидно, подобны. Отсюда на рис. 28,
очевидно, подобны. Отсюда
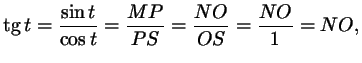 что и утверждалось.
что и утверждалось.
Если точка 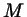 имеет координаты имеет координаты 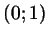 или или 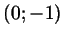 , то прямая , то прямая
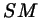 параллельна оси тангенсов, и тангенс нашим способом
определить нельзя. Это и не удивительно: абсцисса этих точек
равна 0, так что параллельна оси тангенсов, и тангенс нашим способом
определить нельзя. Это и не удивительно: абсцисса этих точек
равна 0, так что 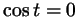 при соответствующих значениях при соответствующих значениях  , и , и
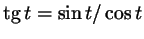 не определен. не определен.
Разберемся, при каких значениях  синус, косинус и тангенс
положительны, а при каких - отрицательны. Согласно определению, синус, косинус и тангенс
положительны, а при каких - отрицательны. Согласно определению,
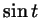 - это ордината точки на тригонометрической окружности,
соответствующая числу - это ордината точки на тригонометрической окружности,
соответствующая числу  . Поэтому . Поэтому 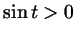 , если точка , если точка  на
окружности лежит выше оси абсцисс, и на
окружности лежит выше оси абсцисс, и 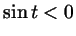 , если точка , если точка  на окружности лежит ниже оси абсцисс (рис. 29а).
на окружности лежит ниже оси абсцисс (рис. 29а).
Рис. 29:
Знаки синуса и косинуса.
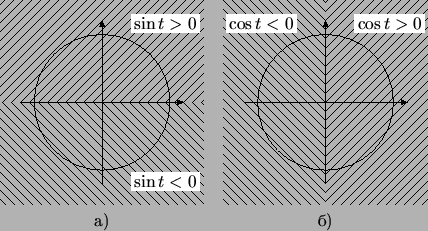 |
На рис. 29б аналогичным образом изображено, когда
положителен и когда отрицателен 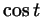 . Увидеть, когда
положителен, а когда отрицателен . Увидеть, когда
положителен, а когда отрицателен
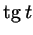 , проще всего с помощью
оси тангенсов: , проще всего с помощью
оси тангенсов:
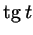 положителен, если точка на окружности,
соответствующая числу положителен, если точка на окружности,
соответствующая числу  , лежит в первой или третьей четверти, и отрицателен, если эта точка лежит во второй или четвертой
четверти. Схематически это изображено на рис. 30а, 30б. , лежит в первой или третьей четверти, и отрицателен, если эта точка лежит во второй или четвертой
четверти. Схематически это изображено на рис. 30а, 30б.
Рис. 30:
Знаки тангенса.
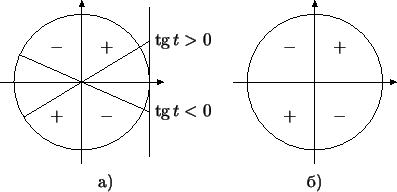 |
Задача 2.15
Нарисуйте картинки, аналогичные рис. 30а, для знаков
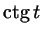 . .
Задача 2.16
а) Изобразите на числовой оси множество точек  ,
удовлетворяющих системе неравенств: ,
удовлетворяющих системе неравенств:
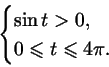
б) Рассмотрим множество чисел на числовой оси,
удовлетворяющих системе неравенств:
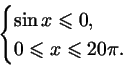 Найдите сумму длин отрезков, из которых состоит это множество.
Найдите сумму длин отрезков, из которых состоит это множество.
Написать комментарий
|

