Next: 2 Определение тригонометрических функций
Up: Начальные свойства тригонометрических функций
Previous: Начальные свойства тригонометрических функций
1 Часы, или современный взгляд на
тригонометрию
До сих пор тригонометрия была для
нас наукой о соотношениях сторон в треугольниках. Именно с этого
развитие тригонометрии и начиналось (слово ``тригонометрия''
означает в переводе с древнегреческого ``измерение
треугольников''). Позднее, однако, акценты сместились, и сейчас
тригонометрию правильнее рассматривать как науку не
о треугольниках, а о периодических процессах. Чтобы понять, при
чем тут периодические процессы, рассмотрим простейший из них -
движение стрелок часов.
Задача 1.1
Предположим, что все стрелки часов имеют длину 1 см (видимо, это
женские наручные часики). Какой путь проходит за сутки:
а)
секундная стрелка;
б)
минутная стрелка;
в)
часовая стрелка?
(Мы имеем в виду, конечно, путь, проходимый концом стрелки.)
Задача 1.2
Секундная стрелка часов имеет длину 1 см. Часы завели
в 12 часов дня 1 января. В котором часу и какого числа
путь, пройденный концом секундной стрелки, составит 1 км?
С какой точностью надо знать пройденный стрелкой путь,
чтобы иметь возможность ответить на вопрос о дате?
Часы нам еще сослужат добрую службу, но чтобы не входить
в противоречие с общепринятой терминологией и обозначениями, нам
нужны часы не совсем обычные. Наши ``часы для любителей
тригонометрии'' имеют всего одну стрелку. Эта стрелка движется
в обратном (по сравнению с обычными часами) направлении. В момент
пуска часов стрелка указывает вправо (туда, где на обычных часах
написана цифра 3). За час стрелка поворачивается на 1 радиан.
Рис. 20:
Часы фирмы ``Тригонометрия''.
 |
Будем считать, что длина стрелки равна 1. Тогда, согласно
определению радианной меры угла, длина дуги, описываемой концом
стрелки за час, равна 1, за два часа - 2 и т.д.
Объясним теперь, какое отношение эти часы имеют к синусам
и косинусам. Для этого рассмотрим систему координат,
расположенную, как показано на рис. 21а.
Рис. 21:
Часы и тригонометрия.
 |
Каковы будут координаты конца стрелки в момент  (через (через  часов после запуска)? Из рис. 21б ясно, что, пока
стрелка не успела выйти за пределы первой координатной четверти,
ее координаты будут
часов после запуска)? Из рис. 21б ясно, что, пока
стрелка не успела выйти за пределы первой координатной четверти,
ее координаты будут
 (имеются в виду косинус и синус угла в (имеются в виду косинус и синус угла в  радиан). В самом деле, из прямоугольного
треугольника радиан). В самом деле, из прямоугольного
треугольника  видно, что видно, что
 , ,
 , а радианная мера угла , а радианная мера угла
 равна равна  . .
Пусть теперь стрелка вышла за пределы первой координатной
четверти (это означает, что пройденный ей путь  превысил превысил
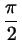 ). Формально мы не можем сказать, что координаты конца
стрелки равны ). Формально мы не можем сказать, что координаты конца
стрелки равны
 , так как , так как  больше не является
радианной мерой острого угла, а синус и косинус мы определили
только для острых углов. Однако мы можем обобщить наши
определения. Можно определить косинус
числа больше не является
радианной мерой острого угла, а синус и косинус мы определили
только для острых углов. Однако мы можем обобщить наши
определения. Можно определить косинус
числа  как абсциссу конца
стрелки в тот момент, когда пройденное этим концом расстояние
составит как абсциссу конца
стрелки в тот момент, когда пройденное этим концом расстояние
составит  . Аналогично синус . Аналогично синус
 определяется как ордината
конца стрелки в тот же момент. Как мы видели, в тех случаях,
когда определяется как ордината
конца стрелки в тот же момент. Как мы видели, в тех случаях,
когда  является радианной мерой острого угла, новые
определения согласуются с прежними. является радианной мерой острого угла, новые
определения согласуются с прежними.
Задача 1.3
Как бы вы определили синус и косинус отрицательного числа  ? ?
Задача 1.4
Найдите:
а)  и и  ; ; |
б)  и и  ; ; |
в)
 и и
 ; ; |
г)
 и и
 . . |
В следующем параграфе мы дадим более формальные определения
синуса и косинуса произвольного числа и начнем систематическое
изучение тригонометрии. Но некоторые важные свойства синуса
и косинуса можно увидеть уже сейчас.
Заметим, что за время  стрелка наших часов делает полный
круг и оказывается на прежнем месте. Поэтому координаты ее конца
в моменты стрелка наших часов делает полный
круг и оказывается на прежнем месте. Поэтому координаты ее конца
в моменты  и и  одинаковы. Другими словами: одинаковы. Другими словами:
Как говорят, функции синус и косинус имеют период  . .
Задача 1.5
Как меняется положение стрелки за время  ? Чему равны ? Чему равны
 и и
 ? ?
Посмотрим теперь, как изменяются 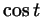 и и 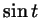 при
изменении при
изменении  . Сделаем это для косинуса (ситуация с синусом
аналогична). . Сделаем это для косинуса (ситуация с синусом
аналогична).
Стрелка часов равномерно вращается, при этом в тот момент, когда
конец стрелки прошел расстояние  , проекция этого конца на ось
абсцисс отмечает число , проекция этого конца на ось
абсцисс отмечает число 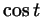 (рис. 22а). Видно, что
эта проекция совершает колебания от (рис. 22а). Видно, что
эта проекция совершает колебания от 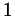 до до  и обратно. Далее,
движение конца стрелки по окружности равномерно, но движение его
проекции равномерным уже не будет. Чтобы это увидеть, нанесем на
окружность положения конца стрелки через равные промежутки
времени, а на ось абсцисс - их проекции (рис. 22б). и обратно. Далее,
движение конца стрелки по окружности равномерно, но движение его
проекции равномерным уже не будет. Чтобы это увидеть, нанесем на
окружность положения конца стрелки через равные промежутки
времени, а на ось абсцисс - их проекции (рис. 22б).
Рис. 22:
Как меняется косинус.
 |
Хорошо видно, что концов отрезка ![$ [-1;1]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img61.gif) точки идут гуще, чем
в его середине. Однако отмеченные точки - не что иное, как
проекции конца стрелки через равные промежутки времени. Стало
быть, в середине отрезка точки идут гуще, чем
в его середине. Однако отмеченные точки - не что иное, как
проекции конца стрелки через равные промежутки времени. Стало
быть, в середине отрезка ![$ [-1;1]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img61.gif) наша точка движется быстрее,
чем у его краев. Это и понятно: в своих колебаниях по отрезку
наша точка в концах разворачивается, а чтобы развернуться, надо
сначала затормозить. наша точка движется быстрее,
чем у его краев. Это и понятно: в своих колебаниях по отрезку
наша точка в концах разворачивается, а чтобы развернуться, надо
сначала затормозить.
Задача 1.6
а) Если для каждого целого 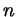 найти число найти число
 ,
сколько различных чисел получится? ,
сколько различных чисел получится?
б*) Каким должно быть число  , чтобы множество чисел вида , чтобы множество чисел вида
 , где , где 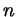 пробегает все целые числа, было конечно? пробегает все целые числа, было конечно?
в**) Существует ли такое натуральное число 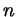 , что , что
 ? ?
Давайте
подсчитаем поточнее, с какой скоростью
движется проекция конца стрелки. Будем опять-таки
рассматривать проекцию на горизонтальную ось,
соответствующую косинусу. Мы считали, что стрелка движется
со скоростью
 и имеет длину 1, так что ее конец
движется со скоростью 1. Пусть в данный момент стрелка и имеет длину 1, так что ее конец
движется со скоростью 1. Пусть в данный момент стрелка
Рис. 23:
 |
повернута на угол  (рис. 23) Через маленькое
время (рис. 23) Через маленькое
время  конец стрелки переместится из точки конец стрелки переместится из точки  в точку в точку
 , а его проекция - из точки , а его проекция - из точки 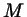 в точку в точку  . Найдем отрезок . Найдем отрезок
 . Для этого заметим, что угол . Для этого заметим, что угол  можно приближенно считать
прямым, так как хорда можно приближенно считать
прямым, так как хорда  мала. Поэтому мала. Поэтому
 (углы измеряются в радианах). Следовательно,
(углы измеряются в радианах). Следовательно,
 Далее, так как хорда
Далее, так как хорда  мала, ее длина приближенно равна длине
дуги мала, ее длина приближенно равна длине
дуги  , то есть , то есть  . Следовательно, . Следовательно,
 , и средняя скорость проекции конца стрелки на
участке от , и средняя скорость проекции конца стрелки на
участке от 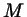 до до  приблизительно равна приблизительно равна
 . На
самом деле чем меньше, тем меньше ошибки наших приближенных
вычислений и тем ближе средняя скорость к . На
самом деле чем меньше, тем меньше ошибки наших приближенных
вычислений и тем ближе средняя скорость к 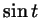 . Как говорят,
мгновенная скорость проекции конца стрелки в тот момент, когда
стрелка прошла расстояние . Как говорят,
мгновенная скорость проекции конца стрелки в тот момент, когда
стрелка прошла расстояние  , равна , равна 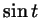 . Точнее говоря,
эта мгновенная скорость равна . Точнее говоря,
эта мгновенная скорость равна  , так как при возрастании
пройденного расстояния от , так как при возрастании
пройденного расстояния от  до до  проекция конца стрелки
движется по оси абсцисс в ``отрицательном направлении'' (от
больших чисел к меньшим). Говоря по-ученому, производная от
функции проекция конца стрелки
движется по оси абсцисс в ``отрицательном направлении'' (от
больших чисел к меньшим). Говоря по-ученому, производная от
функции  - это функция - это функция  . .
Написать комментарий
|

