Next: 6 Простейшие тригонометрические уравнения
Up: Начальные свойства тригонометрических функций
Previous: 4 Периоды тригонометрических функций
Нанесем на тригонометрическую
окружность точку 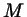 , соответствующую числу , соответствующую числу  . Ее координатами
будут . Ее координатами
будут
 . .
Опустим из точки 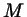 перпендикуляр на ось абсцисс. У нас
получится прямоугольный треугольник (на рис. 33а он
заштрихован). перпендикуляр на ось абсцисс. У нас
получится прямоугольный треугольник (на рис. 33а он
заштрихован).
Рис. 33:
Точка 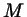 соответствует числу соответствует числу  , точка , точка  соответствует
числу соответствует
числу  . .
 |
Теперь повернем этот треугольник на  против часовой
стрелки. Он займет положение, показанное на рис. 33б.
Точка против часовой
стрелки. Он займет положение, показанное на рис. 33б.
Точка 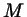 на этом рисунке соответствует числу на этом рисунке соответствует числу  (так как
угол (так как
угол  , очевидно, прямой) и имеет координаты , очевидно, прямой) и имеет координаты
 . Поскольку координаты точки на тригонометрической
окружности - это косинус и синус соответствующего этой точке
числа, получаем такие формулы: . Поскольку координаты точки на тригонометрической
окружности - это косинус и синус соответствующего этой точке
числа, получаем такие формулы:
Поделим эти равенства одно на другое. Получится вот что:
Строго говоря, мы доказали эти формулы лишь в одном случае -
если точка, соответствующая числу  , лежит в первой четверти.
Проверьте сами, что эти формулы верны и в других случаях. , лежит в первой четверти.
Проверьте сами, что эти формулы верны и в других случаях.
Итак, сравнив два положения треугольника на рис. 33а, мы
получили несколько формул. Прикладывать этот треугольник к осям
можно и разными другими способами, и каждый из этих способов дает
свой набор формул. На рис. 34 изображены разные
способы перекладывания треугольника, а под ними выписаны
соответствующие формулы.
Рис. 34:
Формулы
приведения.
 |
Задача 5.1
Заполните пустые места в подписях к чертежам на
рис. 34.
Формулы, которые мы получили с помощью перекладывания
треугольника, называются формулами приведения. Точнее говоря,
пусть у нас есть число  , равное , равное  для какого-то
целого числа для какого-то
целого числа 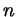 . Формулами приведения называются формулы,
связывающие тригонометрические функции от . Формулами приведения называются формулы,
связывающие тригонометрические функции от  , ,  или или  с тригонометрическими функциями от
с тригонометрическими функциями от  . Как видите, этих формул
много, и заучивать их наизусть было бы неразумно. На практике,
если требуется воспользоваться формулой приведения, удобно
нарисовать картинку наподобие тех, из которых составлен
рис. 34, и посмотреть по ней, как должна выглядеть
формула. Кроме того, есть и мнемоническое правило, позволяющее
выписать любую формулу приведения. Сформулируем это правило. . Как видите, этих формул
много, и заучивать их наизусть было бы неразумно. На практике,
если требуется воспользоваться формулой приведения, удобно
нарисовать картинку наподобие тех, из которых составлен
рис. 34, и посмотреть по ней, как должна выглядеть
формула. Кроме того, есть и мнемоническое правило, позволяющее
выписать любую формулу приведения. Сформулируем это правило.
Пусть в левой
части стоит тригонометрическая функция от  , ,  или или  ,
где ,
где  . Если . Если  укладывается в числе укладывается в числе  целое число
раз ( целое число
раз ( , ,  , ,  , ,  , ,  ...), то в правой
части надо записать ту же тригонометрическую функцию, что
и в левой части. Если же ...), то в правой
части надо записать ту же тригонометрическую функцию, что
и в левой части. Если же  укладывается в числе укладывается в числе  не
целое, а ``полуцелое'' число раз ( не
целое, а ``полуцелое'' число раз ( , , 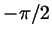 , ,
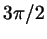 , ,  ...), то название тригонометрической функции
надо заменить на похожее (синус на косинус и наоборот, тангенс на
котангенс и наоборот). ...), то название тригонометрической функции
надо заменить на похожее (синус на косинус и наоборот, тангенс на
котангенс и наоборот).
Если при  , принадлежащем первой четверти, левая часть
положительна, то перед правой частью надо поставить знак плюс, в противном случае - знак минус. , принадлежащем первой четверти, левая часть
положительна, то перед правой частью надо поставить знак плюс, в противном случае - знак минус.
Рис. 35:
 |
Вот как по этим правилам получается формула для
 : :
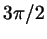 скобках указывает, что название функции меняется, так
что в правой части будет стоять косинус; так как при скобках указывает, что название функции меняется, так
что в правой части будет стоять косинус; так как при  , лежащем в первой четверти, , лежащем в первой четверти,
 отрицателен (рис. 35),
перед косинусом будет стоять знак минус. В итоге: отрицателен (рис. 35),
перед косинусом будет стоять знак минус. В итоге:
 . .
С помощью формул приведения тригонометрические
функции любого числа можно выразить через тригонометрические функции чисел,
лежащих на отрезке ![$ [0;\pi/2]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img106.gif) (от (от  до до  , если
измерять углы в градусах). Поэтому тригонометрические таблицы
составляются только для углов от , если
измерять углы в градусах). Поэтому тригонометрические таблицы
составляются только для углов от  до до  ; в современных калькуляторах и компьютерах программы, вычисляющие
тригонометрические функции, также предварительно ``приводят''
аргумент к промежутку ; в современных калькуляторах и компьютерах программы, вычисляющие
тригонометрические функции, также предварительно ``приводят''
аргумент к промежутку ![$ [0;\pi/2]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img106.gif) . .
Из множества формул приведения стоит, возможно, отметить такие:
Эти формулы называются ``формулами дополнительного угла'';
для острых углов они нам уже знакомы.
Полезно также запомнить, как меняются тригонометрические
функции при изменении знака аргумента:
Иными словами, синус, тангенс и котангенс - нечетные функции,
косинус - четная функция.
Задача 5.2
Упростите выражения:

Задача 5.3
Вычислите:

Задача 5.4
Выразите через тригонометрическую функцию числа, лежащего на
отрезке ![$ [0;\pi/2]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img106.gif) : :

Задача 5.5
Определите знаки следующих выражений:

Задача 5.6
Пусть на плоскости задана система координат и точка 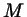 с координатами
с координатами  . Запишите координаты точки, в которую . Запишите координаты точки, в которую 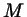 переходит при следующих преобразованиях:
а)
симметрии относительно оси абсцисс;
б)
симметрии относительно оси ординат;
в)
симметрии относительно начала координат;
г)
повороте относительно начала координат на
переходит при следующих преобразованиях:
а)
симметрии относительно оси абсцисс;
б)
симметрии относительно оси ординат;
в)
симметрии относительно начала координат;
г)
повороте относительно начала координат на  в положительном направлении;
д)
симметрии относительно прямой с уравнением в положительном направлении;
д)
симметрии относительно прямой с уравнением  . .
Написать комментарий
|

