Научная Сеть >> "Тригонометрия" И.М. Гельфанд, С.М. Львовский, А.Л. Тоом.

Наука >> Математика >> Алгебра, математическая логика и теория чисел | Книги

Next: 3 Косинус Up: Первое знакомство с тригонометрией Previous: 1 Как измерить крутизну

2 Тангенс

В предыдущем параграфе мы научились измерять крутизну с помощью синуса угла. Есть и другой способ измерения крутизны, составляющий, как пока еще говорят, альтернативу синусу.

Представим себе, что человек, поднимаясь по тропе, приближается к крутому берегу (рис. 8). Если измерять крутизну подъема с помощью отношения высоты подъема к длине пути, то получится уже знакомый нам синус. Давайте теперь вместо длины пройденного человеком пути измерять, насколько он приблизился к берегу по горизонтали. Иными словами, рассмотрим расстояние - проекцию пути на горизонталь. В качестве характеристики крутизны возьмем отношение . Это отношение называется тангенсом угла.

Рис. 8: Тангенс

$\begin{figure}\epsfbox{t02.1}\end{figure}$

Определение. Тангенсом острого угла в прямоугольном треугольнике называется отношение катета этого треугольника, лежащего против угла, к катету треугольника, прилежащему к углу (рис. 9).

Рис. 9: $\mathop{\mathrm{tg}}\nolimits \alpha=BC/AC$

$\begin{figure}\epsfbox{t01.5}\end{figure}$

Как и синус угла, тангенс не зависит от выбора прямоугольного треугольника, содержащего этот угол.

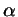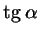Обозначается тангенс угла $\alpha$ так: $\mathop{\mathrm{tg}}\nolimits \alpha$ (читается ``тангенс альфа'').

Задача 2.1 Докажите, что тангенс угла не зависит от размеров прямоугольного треугольника, содержащего этот угол.

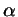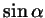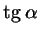Задача 2.2 Для данного острого угла $\alpha$ что больше: $\sin\alpha$ или $\mathop{\mathrm{tg}}\nolimits \alpha$ ?

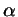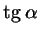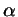Выясним, как связаны синус и тангенс угла. Пусть, например, известен тангенс угла $\alpha$ ; как найти его синус? Воспользуемся тем, что для вычисления $\mathop{\mathrm{tg}}\nolimits \alpha$ годится любой прямоугольный треугольник с углом $\alpha$ ; выберем тот из них, что изображен на рис. 10. По теореме Пифагора его гипотенуза равна $\sqrt{1+\mathop{\mathrm{tg}}\nolimits ^2\alpha}$ , так что

Рис. 10:

$\begin{figure}\epsfbox{t02.3}\end{figure}$

$\displaystyle \sin\alpha=\frac{\mathop{\mathrm{tg}}\nolimits \alpha}{\sqrt{1+\mathop{\mathrm{tg}}\nolimits ^2\alpha}}$

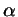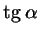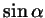Задача 2.3 Пусть $\alpha$ - острый угол; выведите формулу, выражающую $\mathop{\mathrm{tg}}\nolimits \alpha$ через $\sin\alpha$ .

Задача 2.4 Для каждого из углов 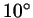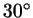$10^\circ$ , $30^\circ$ , $60^\circ$ найдите приближенные значения их тангенса. Что больше: тангенс или радианная мера? И на сколько процентов больше?

Из предыдущей задачи вы должны были увидеть, что тангенсы фигурировавших в ней углов больше, чем их радианная мера. На самом деле это верно для любых острых углов. Наглядно это можно пояснить с помощью рис. 11а. На нем , так что длина дуги равна $2\alpha$ (мы считаем, что угол измерен в радианах), а длина ломаной равна $2\mathop{\mathrm{tg}}\nolimits \alpha$ . Из рисунка ясно, что длина ломаной больше, чем длина дуги , 2 так что $2\mathop{\mathrm{tg}}\nolimits \alpha >2\alpha$ , откуда $\mathop{\mathrm{tg}}\nolimits \alpha >\alpha$ .

Рис. 11:

$\begin{figure}\begin{tabular}{cc} \epsfbox{t02.4}&\epsfbox{t02.5}\\ а) & б) \end{tabular}\end{figure}$

Аккуратное доказательство этого неравенства вы узнаете, решив следующую задачу.

Задача 2.5 Докажите неравенство $\mathop{\mathrm{tg}}\nolimits \alpha >\alpha$ .

Указание. Сравните площадь треугольника и сектора (рис. 11б). Площадь сектора равна половине произведения длины дуги, ограничивающей этот сектор, на радиус окружности.

МЦНМО

Написать комментарий