Next: 4.8. Дискретное логарифмирование
Up: 4. Алгоритмические проблемы теории
Previous: 4.6. Как проверить большое
Contents: Содержание
Мы лишь
кратко коснемся этой темы, отсылая читателей к книгам [6,16,17]. Среди
многих алгоритмов разложения мы выберем ту линию развития, которая привела
к разложению числа, предложенного RSA.
Поиском эффективных способов разложения целых чисел на множители
занимаются уже очень давно. Эта задача интересовала выдающихся ученых в
области теории чисел. Вероятно Ферма был первый, кто предложил представить
разлагаемое число 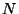 в виде разности квадратов в виде разности квадратов  , а затем, вычисляя , а затем, вычисляя
 , попытаться найти нетривиальный делитель , попытаться найти нетривиальный делитель 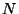 .
Он же предложил и способ,
позволяющий найти требуемое представление. Если разлагаемое число имеет два
не очень отличающиеся по величине множителя, этот способ позволяет
определить их быстрее, чем простой перебор делителей. Лежандр обратил
внимание на то, что при таком подходе достаточно получить сравнение .
Он же предложил и способ,
позволяющий найти требуемое представление. Если разлагаемое число имеет два
не очень отличающиеся по величине множителя, этот способ позволяет
определить их быстрее, чем простой перебор делителей. Лежандр обратил
внимание на то, что при таком подходе достаточно получить сравнение
 |
(17) |
Конечно, не каждая пара чисел, удовлетворяющих ему, позволяет разложить 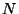 на
множители. Эйлер и Гаусс предложили некоторые способы нахождения чисел,
связанных соотношением (17). Лежандр использовал для этой цели непрерывные
дроби.
на
множители. Эйлер и Гаусс предложили некоторые способы нахождения чисел,
связанных соотношением (17). Лежандр использовал для этой цели непрерывные
дроби.
Напомним, что
каждому
иррациональному числу  может быть поставлена
в соответствие бесконечная последовательность целых
чисел может быть поставлена
в соответствие бесконечная последовательность целых
чисел
 ![$ b_2, \dots]$](http://images.nature.web.ru/nature/2000/12/04/0001157083/img762.gif) ,
называемая его непрерывной дробью. Это сопоставление строится следующим
образом ,
называемая его непрерывной дробью. Это сопоставление строится следующим
образом
![\begin{displaymath}
x_0=\xi, b_i=[x_i], x_{i+1}=\frac{1}{x_i-b_i},\
i=0, 1, 2,\dots.
\end{displaymath}](http://images.nature.web.ru/nature/2000/12/04/0001157083/img763.gif)
Лежандр доказал, что непрерывная дробь квадратичной иррациональности
периодична. Если раскладывать в непрерывную дробь число
 ,
то
возникающие в процессе разложения числа ,
то
возникающие в процессе разложения числа 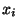 имеют вид
имеют вид
 с целыми с целыми
 , причем всегда , причем всегда
 , ,
 . С каждой непрерывной
дробью можно связать последовательность рациональных чисел, так называемых
подходящих дробей, . С каждой непрерывной
дробью можно связать последовательность рациональных чисел, так называемых
подходящих дробей,
 , ,  , вычисляемых по правилам , вычисляемых по правилам

и
стремящихся к разлагаемому числу. Если в непрерывную дробь разлагается
число  , то справедливо соотношение , то справедливо соотношение
 |
(18) |
из которого следует
 |
(19) |
Заметим, что длина периода разложения в непрерывную дробь числа
 может быть большой и достигать величин порядка
может быть большой и достигать величин порядка  . .
В 1971 г. Шенкс предложил использовать сравнения (19)
для конструирования
чисел, удовлетворяющих (17). Если вычисления проводить до тех пор, пока при
четном 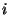 не получится не получится  при некотором целом при некотором целом 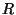 , то пара чисел , то пара чисел
 будет удовлетворять (17) и с ее помощью можно надеяться получить разложение
будет удовлетворять (17) и с ее помощью можно надеяться получить разложение
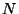 на простые множители. на простые множители.
В 1975 г. Моррисон и Бриллхарт стали перемножать сравнения (19) при
различных 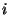 с тем, чтобы таким способом получить квадрат
целого числа в правой
части. Этот метод, метод непрерывных дробей, позволил впервые разложить на
множители седьмое число Ферма с тем, чтобы таким способом получить квадрат
целого числа в правой
части. Этот метод, метод непрерывных дробей, позволил впервые разложить на
множители седьмое число Ферма
 . Для реализации алгоритма
выбирается так называемая
база множителей . Для реализации алгоритма
выбирается так называемая
база множителей
 . В нее входят
ограниченные по величине некоторым параметром простые числа такие, что . В нее входят
ограниченные по величине некоторым параметром простые числа такие, что
 .
Последнее условие связано с тем, что, согласно (18), в разложение на
простые множители чисел .
Последнее условие связано с тем, что, согласно (18), в разложение на
простые множители чисел  могут
входить лишь те простые, для которых могут
входить лишь те простые, для которых 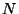 является квадратичным вычетом.
является квадратичным вычетом.
На первом этапе алгоритма каждое очередное число  делится на все
числа делится на все
числа
 и, если оно не разлагается полностью в произведение степеней
этих простых, то отбрасывается. Иначе получается разложение
и, если оно не разлагается полностью в произведение степеней
этих простых, то отбрасывается. Иначе получается разложение
 |
(20) |
Этому номеру 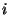 сопоставляется вектор сопоставляется вектор
 (вектор
показателей).
Затем вычисляется
следующее значение (вектор
показателей).
Затем вычисляется
следующее значение  , и с ним проделывается в точности
такая же процедура. , и с ним проделывается в точности
такая же процедура.
Эти вычисления проводятся до тех пор, пока не будет построено  вектора показателей. В получившейся матрице показателей, очевидно, можно
подобрать вектора-строки так, что их сумма будет вектором с четными
координатами
вектора показателей. В получившейся матрице показателей, очевидно, можно
подобрать вектора-строки так, что их сумма будет вектором с четными
координатами
 . Если . Если  - множество номеров векторов, вошедших в
эту сумму, то, как легко проверить с помощью (19), имеет место сравнение - множество номеров векторов, вошедших в
эту сумму, то, как легко проверить с помощью (19), имеет место сравнение

Если с помощью этого сравнения не удается разложить 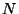 на множители,
разложение в непрерывную дробь продолжается, продолжается набор векторов
показателей и т.д. на множители,
разложение в непрерывную дробь продолжается, продолжается набор векторов
показателей и т.д.
В этот алгоритм был внесен ряд усовершенствований: вместо
 можно
раскладывать в непрерывную дробь число
можно
раскладывать в непрерывную дробь число  , где маленький множитель , где маленький множитель 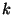 подбирается так, чтобы в базу множителей вошли все малые простые; была
предложена так называемая стратегия раннего обрыва и т.д.
Сложность этого
алгоритма была оценена в 1982 г. величиной
подбирается так, чтобы в базу множителей вошли все малые простые; была
предложена так называемая стратегия раннего обрыва и т.д.
Сложность этого
алгоритма была оценена в 1982 г. величиной
 . При
выводе этой оценки использовался ряд правдоподобных, но не доказанных
гипотез о распределении простых чисел. Получившаяся в оценке функция растет
медленнее любой степенной функции. Алгоритмы, сложность которых
оценивается подобным образом, получили название субэкспоненциальных (в
зависимости от . При
выводе этой оценки использовался ряд правдоподобных, но не доказанных
гипотез о распределении простых чисел. Получившаяся в оценке функция растет
медленнее любой степенной функции. Алгоритмы, сложность которых
оценивается подобным образом, получили название субэкспоненциальных (в
зависимости от  ). ).
В 1982 г. Померанцом был предложен еще один субэкспоненциальный
алгоритм - алгоритм квадратичного решета.
Его сложность оценивается такой же
функцией, как и в методе непрерывных дробей, но вместо константы  получена
лучшая -
получена
лучшая -  . Обозначим . Обозначим
![$ m=\left[\sqrt{N}\right] $](http://images.nature.web.ru/nature/2000/12/04/0001157083/img794.gif) , ,
 и выберем ту же базу
множителей, что и в методе непрерывных дробей. При малых целых значениях и выберем ту же базу
множителей, что и в методе непрерывных дробей. При малых целых значениях 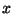 величина
величина  будет сравнительно невелика. Следующий шаг объясняет название
алгоритма - квадратичное решето. Вместо того, чтобы перебирать числа
будет сравнительно невелика. Следующий шаг объясняет название
алгоритма - квадратичное решето. Вместо того, чтобы перебирать числа 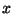 и
раскладывать соответствующие значения
и
раскладывать соответствующие значения  на множители, алгоритм сразу
отсеивает негодные значения на множители, алгоритм сразу
отсеивает негодные значения 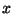 , оставляя лишь те, для которых , оставляя лишь те, для которых  имеет
делители среди элементов базы множителей.
имеет
делители среди элементов базы множителей.
Задав некоторую границу 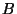 , для каждого простого числа , для каждого простого числа 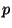 , входящего в
базу множителей, и каждого показателя степени , входящего в
базу множителей, и каждого показателя степени 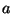 ,
с условием ,
с условием  находим
решения находим
решения 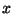 квадратичного сравнения квадратичного сравнения
 . Множество решений
обозначим буквой . Множество решений
обозначим буквой  . Итак, для каждого . Итак, для каждого  найдется элемент базы множителей, а может быть и не один, входящий в
некоторой степени в разложение на простые сомножители числа
найдется элемент базы множителей, а может быть и не один, входящий в
некоторой степени в разложение на простые сомножители числа  .
Те числа .
Те числа 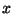 , при которых значения , при которых значения  оказываются полностью
разложенными, дают нам вектор показателей, как и в алгоритме
непрерывных дробей. Если таких векторов окажется достаточно много, с
ними можно проделать те же операции, что и в
алгоритме непрерывных дробей. оказываются полностью
разложенными, дают нам вектор показателей, как и в алгоритме
непрерывных дробей. Если таких векторов окажется достаточно много, с
ними можно проделать те же операции, что и в
алгоритме непрерывных дробей.
Мы кратко описали здесь лишь основную идею алгоритма. Помимо этого,
используется много других дополнительных соображений и различных
технических приемов. Например, аналог соотношения (20) имеет вид
 |
(21) |
В нем допускается наличие двух дополнительных больших простых множителей
 . Эти множители впоследствии при перемножении значений . Эти множители впоследствии при перемножении значений  исключаются.
исключаются.
Некоторые детали реализации алгоритма можно найти в работе [6].
Отметим здесь только, что на множители раскладывалось число  , база
множителей состояла из , база
множителей состояла из  и 524338 простых чисел,
меньших, чем и 524338 простых чисел,
меньших, чем  .
При этом было использовано .
При этом было использовано  . В результате просеивания получилось
112011 соотношений вида (21) без множителей . В результате просеивания получилось
112011 соотношений вида (21) без множителей 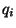 ,
1431337 соотношений с одним
таким множителем и 6881138 соотношений с двумя множителями. Именно на
поиск всех этих соотношений понадобились 220 дней и большое количество
работавших параллельно компьютеров. На втором шаге алгоритма, когда из
соотношений (21) комбинировались четные векторы показателей степеней,
приходилось работать с матрицами, размеры которых измерялись сотнями тысяч
битов. Этот второй шаг потребовал 45 часов работы. Уже четвертый вектор с
четными показателями привел к искомому разложению на множители. ,
1431337 соотношений с одним
таким множителем и 6881138 соотношений с двумя множителями. Именно на
поиск всех этих соотношений понадобились 220 дней и большое количество
работавших параллельно компьютеров. На втором шаге алгоритма, когда из
соотношений (21) комбинировались четные векторы показателей степеней,
приходилось работать с матрицами, размеры которых измерялись сотнями тысяч
битов. Этот второй шаг потребовал 45 часов работы. Уже четвертый вектор с
четными показателями привел к искомому разложению на множители.
Next: 4.8. Дискретное логарифмирование
Up: 4. Алгоритмические проблемы теории
Previous: 4.6. Как проверить большое
Contents: Содержание
Написать комментарий
|

