Next: 3. Способы изображения систем
Up: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Previous: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Contents: Содержание
Чтобы приступить к математическому анализу криптографии,
необходимо ввести удовлетворительную идеализацию и определить
математически приемлемым способом, что будет пониматься под
термином секретная система. Схематическая структура секретной
системы показана на рис. 1.
На передающем конце имеются два источника информации --
источник сообщений и источник ключей. Источник ключей
Рис. 1.
Схема общей секретной системы.
|
отбирает
конкретный ключ среди всех возможных ключей данной
системы. Этот ключ передается некоторым способом на приемный
конец, причем предполагается, что его нельзя перехватить
(например, ключ передается посыльным). Источник сообщений
формирует некоторое сообщение (незашифрованное), которое затем
зашифровывается, и готовая криптограмма передается на приемный
конец, причем криптограмма может быть перехвачена
(например, пересылается по радио). На приемном конце
шифровальщик с помощью ключа по криптограмме восстанавливает
исходное сообщение.
Очевидно, шифровальщик на передающем конце выполняет
некоторую функциональную операцию. Если 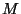 -- сообщение, -- сообщение,
 -- ключ и -- ключ и 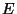 -- зашифрованное сообщение (криптограмма), то
имеем -- зашифрованное сообщение (криптограмма), то
имеем

т.е. 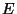 является функцией от является функцией от 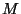 и и  . Удобнее, однако, понимать . Удобнее, однако, понимать 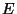 не как функцию двух переменных, а как (однопараметрическое)
семейство операций или отображений, и записывать его в виде:
не как функцию двух переменных, а как (однопараметрическое)
семейство операций или отображений, и записывать его в виде:

Отображение 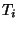 , примененное к сообщению , примененное к сообщению 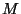 , дает криптограмму , дает криптограмму 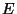 .
Индекс .
Индекс 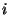 соответствует конкретному используемому ключу. соответствует конкретному используемому ключу.
Вообще мы будем предполагать, что имеется лишь конечное
число возможных ключей, каждому из которых соответствует
вероятность 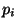 . Таким образом, источник ключей является
статистическим процессом, или устройством, которое выбирает одно
из множества отображений . Таким образом, источник ключей является
статистическим процессом, или устройством, которое выбирает одно
из множества отображений
 с вероятностями с вероятностями  соответственно. Будем также предполагать, что число возможных
сообщений конечно и эти сообщения
соответственно. Будем также предполагать, что число возможных
сообщений конечно и эти сообщения
 имеют априорные
вероятности имеют априорные
вероятности
 . Например, возможными сообщениями могли
бы быть всевозможные последовательности английских букв,
включающих по . Например, возможными сообщениями могли
бы быть всевозможные последовательности английских букв,
включающих по 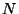 букв каждая, а соответствующими вероятностями
тогда были бы относительные частоты появления таких
последовательностей в нормативном английском тексте. букв каждая, а соответствующими вероятностями
тогда были бы относительные частоты появления таких
последовательностей в нормативном английском тексте.
Должна иметься возможность восстанавливать 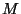 на приемном
конце, когда известны на приемном
конце, когда известны 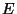 и и  . Поэтому отображение . Поэтому отображение 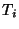 из нашего
семейства должно иметь единственное обратное отображение из нашего
семейства должно иметь единственное обратное отображение  ,
так что ,
так что
 , где , где 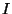 -- тождественное отображение. Таким
образом: -- тождественное отображение. Таким
образом:

Во всяком случае, это обратное отображение  должно
существовать и быть единственным для каждого должно
существовать и быть единственным для каждого 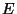 , которое может
быть получено из , которое может
быть получено из 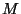 с помощью ключа с помощью ключа 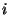 . Приходим, таким образом, к
следующему определению: секретная
система есть семейство
однозначно обратимых отображений . Приходим, таким образом, к
следующему определению: секретная
система есть семейство
однозначно обратимых отображений 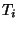 множества возможных
сообщений во множество криптограмм, при этом отображение множества возможных
сообщений во множество криптограмм, при этом отображение 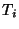 имеет вероятность
имеет вероятность 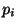 . Обратно, любое множество объектов такого
типа будет называться ``секретной системой''.
Множество возможных
сообщений для удобства будет называться ``пространством
сообщений'', а множество
возможных криптограмм -- ``пространством
криптограмм''. . Обратно, любое множество объектов такого
типа будет называться ``секретной системой''.
Множество возможных
сообщений для удобства будет называться ``пространством
сообщений'', а множество
возможных криптограмм -- ``пространством
криптограмм''.
Две секретные системы
совпадают, если они образованы одним и
тем же множеством отображений 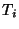 и одинаковыми пространствами
сообщений и криптограмм, причем вероятности ключей в этих
системах также совпадают. и одинаковыми пространствами
сообщений и криптограмм, причем вероятности ключей в этих
системах также совпадают.
Секретную систему можно представлять себе как некоторую
машину с одним или более переключающими устройствами.
Последовательность букв (сообщение) поступает на вход машины, а
на выходе ее получается другая последовательность. Конкретное
положение переключающих устройств соответствует конкретному
используемому ключу. Для выбора ключа из множества возможных
ключей должны быть заданы некоторые статистические методы.
Для того чтобы нашу проблему можно было рассмотреть
математически, предположим, что противнику известна
используемая система. Иными словами, он знает семейство
отображений 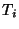 и вероятности выбора различных ключей. Можно было
бы, во-первых, возразить, что такое предположение нереалистично,
так как шифровальщик противника часто не знает, какая система
использовалась или чему равны рассматриваемые вероятности. На
это возражение имеется два ответа. и вероятности выбора различных ключей. Можно было
бы, во-первых, возразить, что такое предположение нереалистично,
так как шифровальщик противника часто не знает, какая система
использовалась или чему равны рассматриваемые вероятности. На
это возражение имеется два ответа.
1. Наложенное ограничение слабее, чем кажется с первого
взгляда, из-за широты нашего определения секретной системы.
Предположим, что шифровальщик перехватывает сообщение и не
знает, использовалась ли здесь подстановка, или
транспозиция,
или шифр типа Виженера. Он может считать,
что сообщение
зашифровано с помощью системы, в которой часть ключа является
указанием того, какой из трех типов имеющихся ключей был
использован, а следующая часть -- конкретный ключ этого типа.
Указанным трем различным возможностям шифровальщик
приписывает вероятности, учитывая при этом все имеющиеся у него
сведения об априорных вероятностях использования шифровальщиком
противника соответствующих типов шифров.
2. Наше ограничение обычно в криптографических исследованиях.
Оно является пессимистичным, но безопасно, и в конечном счете
реалистично, так как можно ожидать, что противник рано или
поздно раскроет любую секретную систему. Поэтому даже в том
случае, когда разработана совершенно новая система, так что
противник не может приписать ей никаких априорных вероятностей, если
только он ее уже не раскрыл, нужно иметь в виду его возможную
осведомленность.
Эта ситуация аналогична ситуации, возникающей в теории
игр,
где предполагается, что партнер
``обнаруживает'' используемую стратегию игры. В обоих случаях это
предположение служит для более четкого описания сведений, которыми
располагает противная сторона.
Второе возможное возражение против нашего определения
секретной системы состоит в том, что в нем не принимаются в
расчет используемые обычно на практике вставки в сообщение
посторонних нулевых знаков и использование многократных
подстановок. В таких случаях для данного сообщения и ключа
имеется не единственная криптограмма и шифровальщик может
выбрать по своему желанию одну из нескольких различных
криптограмм. Эту ситуацию можно было бы рассмотреть, но это
только внесло бы дополнительные усложнения на данном этапе
рассуждений без существенного изменения каких-либо из основных
выводов.
Если сообщения создаются марковским процессом,
то вероятности разных сообщений определяются
структурой этого марковского процесса. Однако подойдем к вопросу с
более общей точки зрения и будем трактовать сообщения просто как
абстрактное множество объектов, которым приписаны вероятности, причем
эти объекты не обязательно состоят из последовательностей букв и не
обязательно создаются марковским процессом.
Следует подчеркнуть, что далее во всех случаях секретная
система означает не одно, а целое множество отображений. После
того как выбран ключ, используется только одно из этих
отображений и отсюда можно было бы прийти к определению
секретной системы как единственного преобразования языка. Однако
противник не знает, какой ключ выбран, и остальные возможные
ключи столь же важны для него, как и истинный. Именно
существование этих других возможных ключей и придает системе
секретность. Так как мы интересуемся в первую очередь
секретностью, то вынуждены предпочесть данное нами определение
понятия секретной системы. Тип ситуации, когда остальные
возможности так же важны, как и осуществившаяся, часто
встречается в стратегических играх. Ход шахматной игры в
большой степени контролируется угрозами, которые не
осуществляются. Нечто подобное представляет из себя ``фактическое
существование'' нереализованных возможностей в теории игр.
Следует отметить, что система, состоящая из единственной
операции над языком, представляет собой при нашем
определении вырожденный тип секретной системы. Это -- система с
единственным ключом, который имеет вероятность, равную единице.
В такой системе нет секретности -- шифровальщик противника находит
сообщение, применяя к перехваченной криптограмме обратное
отображение, также единственное в такой системе. В этом случае
шифровальщик противника и шифровальщик получателя информации
располагают одинаковой информацией. В общем же случае
единственное различие их сведений состоит в том, что последнему
известен конкретно использовавшийся ключ, в то время как первому
известны лишь априорные вероятности различных ключей из данного
множества. Процесс расшифровки для получателя информации состоит
в применении к криптограмме отображения, обратного по отношению к
конкретному отображению, использованному для составления криптограммы.
Процесс расшифровки для противника представляет собой попытку
определить сообщение (или конкретный ключ),
имея в распоряжении только
криптограмму и априорные вероятности различных ключей и сообщений.
Существует много трудных эпистемологических вопросов, связанных с
теорией секретности, или вернее с любой теорией, связанной с реальным
применением вопросов теории вероятностей (так обстоит дело, в
частности, с априорными вероятностями,
теоремой Байеса и т.д.).
Трактуемая абстрактно теория вероятности может быть изложена на строгих
логических основах с использованием современной теории
меры.
Однако в применениях к физическим ситуациям,
особенно когда дело касается ``субъективных'' вероятностей и
неповторимых экспериментов, возникают многочисленные вопросы, связанные
с логическим обоснованием. Например, при нашем подходе к проблеме
секретности допускается, что априорные вероятности различных ключей и
сообщений известны шифровальщику противника, но как он может определить
их эффективным способом даже при использовании всех своих сведений о
данной обстановке?
Можно создать искусственные криптографические ситуации типа ``урны и
игральной кости'', в которых априорные вероятности имеют вполне
определенный смысл и идеализация, использованная здесь, является
наверняка подходящей. Но в других случаях, которые можно себе
представить, например, при перехвате сообщений, передаваемых между собой
марсианами, высадившимися на Землю, априорные вероятности были бы
настолько неопределенными, что не имели бы никакого значения.
Наиболее часто встречающиеся на практике криптографические задачи лежат
где-то между этими крайними пределами. Шифровальщик противника может
иметь желание разделить возможные сообщения на категории
``приемлемых'', ``возможных, но малоправдоподобных'' и ``неприемлемых'',
но чувствуется, что более подробное подразделение не
имело бы смысла.
К счастью, на практике только очень большие ошибки в априорных
вероятностях ключей и сообщений могут вызвать заметные ошибки в важных
параметрах. Это происходит из-за того, что число сообщений и
криптограмм ведет себя как экспоненциальная функция, а измеряется
логарифмической мерой.
Next: 3. Способы изображения систем
Up: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Previous: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Contents: Содержание
Написать комментарий
|

