Корректное обоснование
тектонофизические методы исследований получили только после работ М.В. Гзовского,
В.В. Белоусова (Гзовский, 1975; Гзовский,
Белоусов, 1964) и Рамберга (1985). В них были
описаны общие условия подобия, что позволило за счет свойств материалов используемых
в моделировании привести в соответствие несопоставимые до этого момента величины
времени деформаций и размеров природных объектов и модельных. Такие материалы
получили название эквивалентных.
Общие критерии подобия
можно представить как (Белоусов и др., 1988):
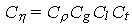 , ,
где 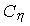 - множитель подобия вязкости, - множитель подобия вязкости,
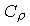 - множитель подобия плотности, - множитель подобия плотности, 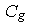 - множитель подобия ускорения свободного падения,
- множитель подобия ускорения свободного падения, 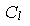 - множитель подобия размера,
- множитель подобия размера, 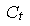 - множитель подобия времени
(множитель подобия определяется как отношение соответствующего параметра в модели
и природном объекте). Поскольку при моделировании без центрифуги - множитель подобия времени
(множитель подобия определяется как отношение соответствующего параметра в модели
и природном объекте). Поскольку при моделировании без центрифуги 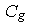 = 1, а = 1, а 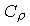 близок к единице (плотности
горной породы и эквивалентного материала отличаются не более чем в 2-3 раза),
то: близок к единице (плотности
горной породы и эквивалентного материала отличаются не более чем в 2-3 раза),
то:
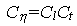 . .
Эту формулу можно
также записать следующим образом:
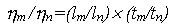 , ,
где 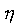 - вязкость, - вязкость, 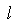 - размеры, - размеры, 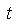 - время, а индексы m и n обозначают, соответственно, модель (model)
и природный объект (nature) (Белоусов и др., 1988). Точность подобных оценок
соответствует порядку величин (10b).
- время, а индексы m и n обозначают, соответственно, модель (model)
и природный объект (nature) (Белоусов и др., 1988). Точность подобных оценок
соответствует порядку величин (10b).
Таким образом, критерии
подобия позволяют оценить соотношения между факторами, определяющими протекание
деформационного процесса (напряжение, деформационные свойства материала, время,
размеры), в модели и природном объекте. Процессы деформации модели и природного
объекта можно считать подобными, если соотношения этих параметров сохраняются
в эксперименте и природе.
Основным свойством
материалов при изучении пластичных деформаций является их низкая вязкость. В
экспериментах используются влажная глина, густые смазочные масла, канифоль и
битум, смешанные с маслом, и др. Вязкость таких веществ на несколько порядков
отличается от вязкости горных пород. В относительно кратковременных экспериментах,
продолжающихся обычно не более нескольких часов, иногда нескольких суток, на
небольших приборах размером первые десятки сантиметров, деформация "текучих"
и "пластичных" эквивалентных материалов подобна природным аналогам,
в которых изучаемый объект может достигать размеров в десятки и сотни километров
при времени деформации составляющем миллионы лет.
Для изучения хрупких
деформаций применяют материалы, которые легко разрушаются в условиях эксперимента
при приложении внешних усилий. К числу таких материалов относится песок, смешанный
с машинным маслом или пушечной смазкой, которые обеспечивают связность сыпучего
материала модели (Белоусов и др., 1988; Гзовский, 1975).
Для анализа напряженного
состояния в хрупко-упругой области применяются модели, изготовленные из оптически
активных материалов (Нетребко, 1988; Бондаренко,
1990; и др.). Основным свойством последних является способность изменять оптические
свойства в зависимости от величины действующих напряжений. В поляризованном
свете это свойство реализуется в виде картины изохроматических полос, по которым
рассчитываются величины напряжений в различных участках модели.
В последние десятилетия
поведение деформируемых объемов пытаются воспроизвести с помощью численного
моделирования. Хорошо справляясь с решением ряда простых задач, методы численного
моделирования на данный момент вряд ли применимы для воспроизведения поведения
многокомпонентных и неоднородно построенных геологических объектов.
Таким образом, изучение
генетических аспектов образования тех или иных структур имеют вполне реальную
методически основу. Благодаря развитию теории подобия, масштабный диапазон этих
структур очень велик - от микроструктур до структур региональных (Белоусов и др., 1988, Талицкий,
1994, Талицкий, Галкин, 1989, 1997). Методами тектонофизического моделирования были
воспроизведены и изучены такие геологические структуры как межзерновой кливаж
(Белоусов и др., 1988), кливаж плойчатости (Талицкий,
1992), кинк-зоны (Андерсон, 1974), будины (Рэмзи,
1967), трещины отрыва (Талицкий, 1992), складки
(Белоусов и др., 1988), разрывы (Белоусов
и др., 1988; Стоянов, 1977), надвиговые дуплексы (Гончаров и др., 1997), зоны транспрессии и транстенсии
(Морозов, Гептнер, 1997), присдвиговые грабены
или бассейны типа pull-apart (Макклей, Дули, 1995),
купольные структуры (Виджак, Шайнер, 1982, Паркер,
Мак-Дауэлл, 1955) и процессы конвекции (Рамберг,
1985).
Таким образом, при
полноценном геологическом анализе, вне зависимости от масштаба исследований,
одним из важных методов исследования является тектонофизическое моделирование.
Следовательно, тектонофизическое моделирование может служить основой для интерпретации
образования тех или иных деформационных структур и их сочетаний - парагенезов.
Тем не менее, всегда следует учитывать, что тектонофизическое моделирование
никогда в точности не воспроизводит природную структуру, что оно "не
доказывает, как возникла та или иная тектоническая деформация, а лишь подсказывает,
как она могла образоваться" (Белоусов, 1985).
|

