|
[Павлов Д.С.] <Математический алгоритм построения
геологических разрезов> [оглавление]
Вероятно, это самый первый метод построения разреза, который
получил научное обоснование. Метод был предложен практически одновременно в
20-ых - начале 30-ых годов английским геологом Баском и российским ученым
Вебером. Метод применяется для концентрических складок с округлыми зонами
шарниров. На картах такие складки характеризуются постепенным изменением углов
падения на крыльях складок.
Суть метода изображена на рисунке 2.1. Предполагается, что нам
известны элементы залегания слоев в точках A, B и C.
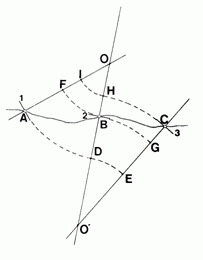 |
| Рисунок 2.1 Построение разреза по методу Баска-Вебера (Marshak, Mitra, 1988). |
Рассмотрим последовательность действий, необходимых для
построения разреза. Сначала проводим перпендикуляры к элементам залегания,
вынесенным на профиль, и находим точки пересечения перпендикуляров к соседним
элементам залегания. Затем, из точек пересечения двух перпендикуляров между
ними строим дуги окружностей через соответствующие элементы залеганий. Дуги
<оборванных> слоев достраиваем, пользуясь тем же методом.
Данный метод допускает введение поправок, если его
непосредственное применение приводит к ошибкам. Пример такого случая приведен
на рисунке 2.2. Здесь предполагается, что нам известны элементы залегания в
точках A, B, C и D. Предполагается, что в точках A и D выходит один и тот же
горизонт, прослеживание горизонта из точки A приводит нас в точку G, но не D.
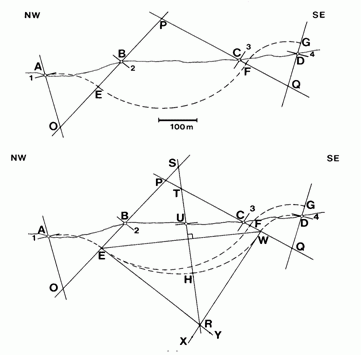 |
| Рисунок 2.2. Введение поправок в метод Баска-Вебера (Marshak, Mitra, 1988). |
Здесь поправка вводится на участке, где мы имеем наименьшее
число наблюдений, то есть наибольшую дугу круга. Скорректированный разрез
строится следующим образом.
Обычным способом строятся дуги из точек A и G. На соседних
перпендикулярах получаем точки E и W, которые соединяем прямой линией EW. Далее
через точки E и W проводятся касательные к проведенным дугам кругов, то есть
перпендикуляры к линиям OE и QC. Перпендикуляры пересекаются в точке R, из
которой на линию EW опускается перпендикуляр, пересекающий уже построенные
радиусы в точках T и S. Дуги EH и HW отстраиваются так, как если бы точки S и T
были бы центрами соответствующих окружностей. При этом перпендикуляр к прямой
RTS в точке U является предполагаемым элементом залегания, необходимым для
соединения горизонта, обнажающегося в точках A и D.
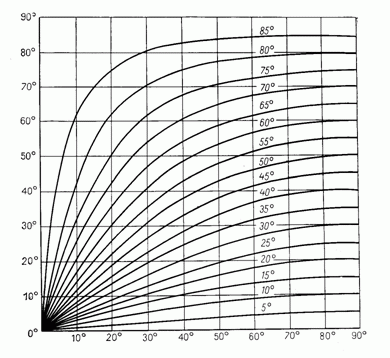 |
| Рисунок 2.3. Номограмма для определения угла наклона в косом разрезе. Кривые -
истинные углы падения, по оси Y (ординат) углы наклона слоев в косом разрезе,
по оси X (абсцисс) углы между простиранием пласта и линией разреза (Михайлов,
1974). |
Метод Баска-Вебера может быть применен как к профильным, так и к
косым сечениям. В последнем случае, однако, на профиль должны выноситься не
истинные элементы залегания, а кажущиеся углы наклона, которые можно рассчитать
по номограмме на рисунке 2.3. Данная номограмма может использоваться в
различных случаях, когда необходимо определить кажущиеся углы падения.
Метод Баска-Вебера дает хорошие результаты в полосе между самыми
ближними точками, принимаемыми за центры окружностей, из которых проводятся
дуги кругов разного радиуса. За их пределами появляются остроугольные точки с
бесконечной кривизной (сингулярные точки), а сама структура изображается
пологой. Пример такого эффекта представлен на рисунке 2.4.
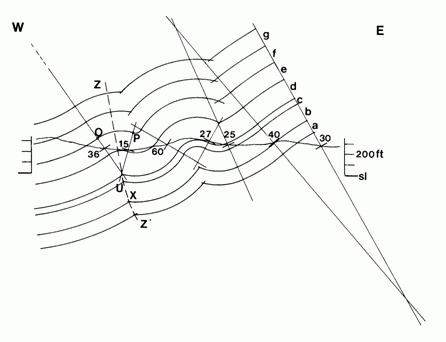 |
| Рисунок 2.4. Эффект выполаживания при использовании метода Баска-Вебера
(Marshak, Mitra, 1988). |
[назад] [оглавление] [далее]
|

