|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
I.3.2. Основные формулы сферической
тригонометрии
Теорема
косинусов. Теорема косинусов, впервые
доказанная Альбатегнием в Х в., устанавливает
зависимость между тремя сторонами (а, в, с) и
одним из углов (А, В или С) сферического
треугольника.
Косинус стороны сферического
треугольника равняется произведению косинусов
двух других его сторон, сложенному с
произведением синусов тех же сторон на косинус
угла между ними:
cos a = cos в . cos c + sin в .
sin c . cos A.
Докажем эту теорему.
Пусть АВС - сферический треугольник (рис. 7), стороны в и с которого
меньше 90o . Соединив его вершины с центром
сферы О, получим центральные углы а, в и с,
пропорциональные величинам дуг, на которые они
опираются, и численно равные сторонам
сферического треугольника: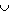 СВ = а, СВ = а, 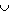 АС = в, АС = в, 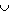 АВ = с. АВ = с.
Сферический угол, например между
дугами СА и АВ (угол САВ), измеряется углом между
касательными к этим дугам (АМ и АN) в точке их
пересечения (А). Пересечения этих касательных с
продолжениями радиусов ОВ и ОС дадут точки М и N.
Из возникших плоских треугольников АМN и ОМN по
формуле косинусов находим
MN2 = AM2 + AN2 - 2 AM . AN
. cos A,
MN2 = OM2 + ON2 - 2 OM . ON
. cos a,
откуда
АМ2 + AN2 - 2 AM . AN .
cos A =
= OM2 + ON2 - 2 OM . ON .
cos a,
2 OM . ON . cos a = OM2 + ON2 - AM2
- AN2 + 2AM . AN . cos A. (1)
Из плоских прямоугольных
треугольников АОМ и AON следует
ОМ2 = ОА2 + АМ2 и ON2
= OA2 + AN2.
Подставив эти значения в правую часть
равенства (1), получим
2 ОМ . ON . cos a = OA2 + AM2
+ OA2+ AN2 - AM2 - AN2 +
+ 2 AM . AN . cos A,
OM . ON . cos a = OA2 + АМ .
AN . cos A. (2)
Из полученного равенства (2) найдем
выражение для cos a:
cos a = 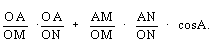 (3) (3)
Из рис. 7 видно, что
 cos c, cos c, 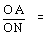 cos в, cos в,  sin c, sin c,  sin в. sin в.
Подставив эти значения в формулу (3),
получим
cos a = cos с . cos в + sin с .
sin в . cos A,
что и требовалось доказать.
Аналогично выводятся формулы для
сторон в и с сферического треугольника
АВС:
cos b = cos a . cos c + sin a .
sin c . cos B,
cos c = cos a . cos в + sin a .
sin в . cos C.
Следует оговорить, что выведенные
формулы для сферических треугольников со
сторонами в и с, меньшими 90o , могут
быть использованы и для треугольников со
сторонами любой длины.
Из формул косинусов сторон
сферического треугольника (а, в, с) выводятся
все необходимые в дальнейшем формулы
сферической тригонометрии. Например, формулы
косинусов углов сферического треугольника (А, В
или С) получаются при помощи введения полярного
треугольника, т.е. треугольника А'В' С' (рис. 8), вершины которого служат
полюсами сторон (дуг) исходного сферического
треугольника АВС. Угол А данного сферического
треугольника АВС и соответствующая ему сторона а'
полярного с ним треугольника А'В' С'в сумме
составляют 180o , т.е. А + а'= 180o .
Для доказательства этого положения
обратимся к рис. 8. Продолжим
стороны АВ и АС сферического треугольника АВС до
пересечения со стороной B'C' полярного с ним
треугольника A'B'C' в точках М и N. Так как вершина А
есть полюс дуги B'C' , то дуга MN служит мерой угла А:
А = MN1). Дуга В' С' ,
соответствующая стороне а' полярного
треугольника, разбита точками М и N на три части,
т.е. а' = B' M + MN + NC' . Cледовательно, А + а' = В' М
+ MN + MN + + NC' = B' N + MC' . А так как точки В' и С' служат
полюсами дуг АС и АВ соответственно, то 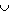 B' N = 90o , B' N = 90o , 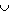 MC' = 90o .
Следовательно, А + а' = 90o + 90o = 180o
, что и требовалось доказать. Таким образом, MC' = 90o .
Следовательно, А + а' = 90o + 90o = 180o
, что и требовалось доказать. Таким образом,
А + а' = 180o ,
В + в' = 180o , (4)
С + с' = 180o .
Аналогично доказывается и положение о
том , что сторона (а) данного сферического
треугольника и соответствующий ей угол
полярного с ним треугольника (А' ) в сумме
составляют 180o , т.е.
а + А'= 180o ,
в + В' = 180o , (5)
с + С' = 180o .
Выведенные особенности взаимно
полярных сферических треугольников позволяют
распространить формулы для сторон сферического
треугольника с соответствующими изменениями на
его углы, и наоборот. Hапример, взяв за основу
формулу косинуса стороны сферического
треугольника
cos a' = cos в' . cos c' + sin в' .
sin c' . cos A'
и учтя только что выведенные
закономерности (4) и (5), можем записать
cos(180o - A) = cos(180o - B) . cos(180o
- C) +
+ sin(180o - B) . sin(180o - C) .
cos(180o - a).
После приведения тригонометрических
функций получаем
- cos A = cos B . cos C - sin B .
sin C . cos a ,
или
cos A = - cos B . cos C + sin B .
sin C . cos a. (6)
Следовательно, косинус угла
сферического треугольника равен произведению
косинусов двух других его углов, взятому с
обратным знаком, сложенному с произведением
синусов тех же углов на косинус стороны между
ними.
Отсюда соответственно
cos a = , ,
cos в =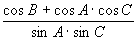 , (7) , (7)
cos c = 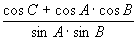 . .
Таким образом, по трем известным углам
А, В и С сферического треугольника АВС могут быть
вычислены все три его стороны а, в и с.
Подставив в полученные формулы (7)
значения элементарных углов поворота
пересекающихся поворотных осей симметрии,
получим их (углов) кристаллографическую запись:

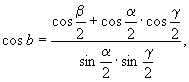 (8) (8)
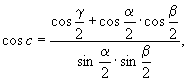
где а, в, с - стороны сферического
треугольника - служат мерами углов между
пересекающимися осями симметрии.
Теорема синусов.
Для решения наиболее реальной
кристаллографической задачи, когда известны
порядки двух пересекающихся под определенным
углом осей симметрии и требуется определить
положение и порядок третьей - результирующей -
оси, необходимо знание еще одной теоремы
сферической тригонометрии - теоремы синусов для
сферического треугольника.
Синусы сторон сфери-ческого
треугольника АВС пропорциональны синусам
его углов:
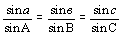 . .
Для доказательства этой теоремы
соединим вершины сферического треугольника АВС (рис. 10) с центром сферы О, в результате
чего возникнет трехгранный угол ОАВС. Из вершины
С опустим перпендикуляр СD на противоположную
грань ОАВ трехгранного угла. Из полученной точки
D опустим перпендикуляры DN и DM на радиусы ОА и ОВ и
соединим прямыми точку С с точками M и N.
Из элементарной геометрии следует, что
CN OA ( так
как DN OA ( так
как DN OA) и
СМ OA) и
СМ  ОВ
(так как DM ОВ
(так как DM OB). Таким образом, угол CND - это линейный угол
двугранного угла СОАВ , соответствующий углу А
рассматриваемого сферического треугольника.
Точно так же угол CMD - сферический угол В.
OB). Таким образом, угол CND - это линейный угол
двугранного угла СОАВ , соответствующий углу А
рассматриваемого сферического треугольника.
Точно так же угол CMD - сферический угол В.
Из рассмотрения прямоугольных
треугольников NDC и МDC с общим катетом CD получим
CM . sin B = CN . sin A. (9)
Отрезки CM и CN можно выразить,
рассмотрев прямоугольные треугольники ОМС и ONC.
Углы МОС и NOC при общей вершине О этих
треугольников соответствуют сторонам а и в сферического
треугольника АВС. На основании этого можно
записать
CM = OC . sin a, CN = OC . sin в.
Подставив эти выражения в равенство (9),
получим
OC . sin a . sin B = OC . sin в
. sin A.
Откуда sin a . sin B = sin A . sin в,
т.е.  Аналогично можно
получить Аналогично можно
получить 
Следовательно,
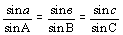 , (10) , (10)
что и требовалось доказать.
Пример. Пусть даны два угла
сферического треугольника и сторона между ними:
А, В и с . Необходимо найти третий угол С и две
стороны а и в.
Угол С находим по формуле косинусов (6):
cos C = - cos A . cos B + sin A . sin B .
cos c
и далее а и в - по формуле
синусов (10):
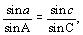 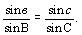
Откуда  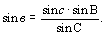
| 
