|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
I.5. Основные положения теории групп
? помощью матриц, как было показано
выше, можно представлять любые симметрические
операции (преобразования) и, находя их
произведения, получать множества матриц,
образующих системы с одной операцией (операцией
умножения), называемые группами. Таким
образом, главная особенность симметрических
операций состоит в том, что полная их
совокупность для любого объекта всегда образует
группу. Это позволяет теорию симметрии
кристаллов рассматривать как раздел
математической теории множеств и использовать
математический аппарат теории абстрактных групп
при изучении законов симметрии кристаллов,
придавая им конкретное геометрическое или
физическое содержание.
Группой называется
множество объектов (G) любой природы с заданной
бинарной операцией (* ), если для любой пары
элементов gi и gj этого множества G
определен третий результирующий элемент gk =
gi * gj того же множества (группы). В
общем случае gi * gj  gj * gi. Это
значит, что результат зависит от того, в какой
последовательности производится умножение
элементов группы. Применительно к операциям
симметрии это означает, что результирующие
операции могут оказаться различными, если
переменить порядок выполнения исходных
операций. Однако группой может называться лишь
такое множество с заданной бинарной операцией,
для которого выполняются следующие условия: gj * gi. Это
значит, что результат зависит от того, в какой
последовательности производится умножение
элементов группы. Применительно к операциям
симметрии это означает, что результирующие
операции могут оказаться различными, если
переменить порядок выполнения исходных
операций. Однако группой может называться лишь
такое множество с заданной бинарной операцией,
для которого выполняются следующие условия:
- ассоциативности - (gi * gj) * gl
= gi * (gj * gl);
- существования единицы - такого
единичного элемента (e), что для любого элемента gi,
принадлежащего группе, будет выполняться
равенство e * gi = gi * e = gi ;
- обратимости - для любого элемента gi
существует единственный элемент gi-1
из того же множества, называемый обратным
элементу gi, такой , что gi * gi-1
= gi-1 * gi = e.
Mожно привести следующие примеры
групп.
1. Ряд целых чисел с операцией сложения.
2. 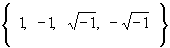 с
операцией умножения. с
операцией умножения.
3. Множество векторов в пространстве с
операцией векторного произведения.
4. Множество матриц с операцией
умножения:

5. Совокупность операций симметрии
некоторого объекта с операцией умножения (=
взаимодействия): {1, 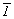 , 2y, my}. , 2y, my}.
?аким образом, теория абстрактных
групп применительно к теории симметрии
кристаллов, по существу, является теорией групп
симметрии, широко использующей математический
аппарат, ибо с математической точки зрения
совокупность операций симметрии удовлетворяет
понятию групп, в которых групповому умножению
соответствует взаимодействие элементов
симметрии 1.
?руппа может содержать один, несколько
или бесконечное число отличных друг от друга
элементов. Порядок группы n - это число ее
элементов. Группа называется конечной, если n
конечно.
Если произведение любой пары
элементов группы не зависит от порядка
сомножителей, то группа называется коммутативной
или абелевой. Если между элементами двух
групп можно установить взаимно однозначное
соответствие, при котором произведению любых
двух членов одной группы отвечает произведение
соответствующих членов другой группы, то такие
группы называются изоморфными. Например,
группы G = {g1, g2, g3, ..., gn} и H =
{h1, h2, h3 ..., hn} изоморфны,
т.е. G<--> H, если gi <--> hi, gj<-->
hj, ..., gigj<--> hihj.
Порядок изоморфных групп одинаков. Изоморфные
друг другу конкретные группы симметрии с точки
зрения теории групп не различаются, хотя их
элементы могут быть различны геометрически.
Отсюда все закономерности, установленные для
одной из абстрактных групп, справедливы и для
всех изоморфных с ней конкретных групп
симметрии, и в этом заключается обобщающее
значение теории групп.
Поскольку все закономерности сводятся
к закону "умножения" элементов, структура
конечной группы - ее порядок - выявляется
произведением любых пар ее членов, собранных в
своеобразную "таблицу умножения", называемую квадратом Кейли (Cayley). В
такой квадратной таблице все операции симметрии,
составляющие группу, начиная с единичного члена,
записываются по горизонтали и вертикали,
произведения же их - на пересечении
вертикального столбца и горизонтальной строки.
Например,
| |
1 |
1 |
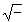 1 1
|
- 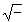 1 1 |
|
|
1 |
mx |
my |
2z |
1 |
1 |
- 1 |
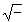 1 1
|
- 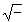 1 1 |
1 |
1 |
mx |
my |
2z |
- 1 |
- 1 |
1 |
- 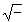 1 1 |
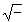 1 1
|
mx |
mx |
1 |
2z |
my |
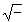 1 1
|
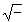 1 1
|
- 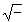 1 1 |
1 |
- 1 |
my |
my |
2z |
1 |
mx |
- 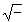 1 1 |
- 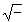 1 1 |
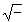 1 1
|
- 1 |
1 |
2z |
2z |
my |
mx |
1 |
Изоморфные группы имеют одинаковые
таблицы умножения (с точностью до перестановок).
Если в группе G имеется такой член gi,
совокупность степеней которого образует все
элементы группы, т.е. G = {g1, g2, ..., gn
= e}, то такая группа называется циклической
и ее порядок равен n. При этом элемент gi,
степенями которого являются все другие члены
группы, называется порождающим элементом или
генератором группы. Если же группа не
циклическая, то в ней можно выделить несколько
порождающих элементов, степени и произведения
которых дают все элементы группы G. Такая
минимальная совокуп-ность элементов называется совокупностью
образующих элементов группы. Однако для
полного задания группы помимо образующих
элементов нужно знать некоторые соотношения
между ними (т.е. их взаимное расположение),
которые называются определяющими
соотношениями (см. табл. 2).
Если часть членов группы G образует
относительно той же операции группу H, то такое
подмножество H называется подгруппой данной
группы. Например, в группе 6-го порядка 32 {1, 31,
32, 2x, 2y, 2u} можно
выделить подгруппу 3-го порядка 3 {1, 31, 32}
или подгруппы второго порядка 2 {1,2x }
и т.д.
Порядок подгруппы (nH)
является делителем порядка конечной группы (nG):
nG/nH = p (теорема Лагранжа); p
называют индексом подгруппы (или, в теории
групп симметрии, кратностью правильных систем
точек, см. с. 233). С другой стороны, можно сказать,
что группа G является надгруппой ?руппы H или
что группа G является расширением группы H.
|

