Экспериментальное изучение граничных эффектов на границе кристалл-расплав

Псевдостационарное состояние роста кристалла

Для упрощения системы рассмотрим диффузию в двухкомпонентной одномерной системе (компонент - разбавитель) с коэффициентом диффузии не зависящим от концентрации, которая описывается законами Фика и изменение концентрации мы можем записать как

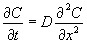(0)

При начальных условиях 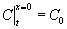(концентрация в точке с координатой х = 0 постоянна) и 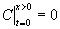решение может быть представлено сходящимся степенным рядом [11]:

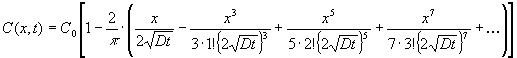(1)

Возьмем в качестве приближения два первых члена этого ряда и получим:

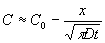(2)

Тогда, фронт диффузии x_f (как координата, в которой концентрация компонента становится неотличимой от нуля):

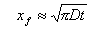(3)

Примем, что скорость роста (R) кристалла постоянна. Тогда координата границы растущего кристалла определяется выражением

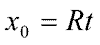(4)

где: R - скорость роста кристалла (см/с).

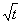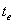При сравнении уравнений (3) и (4) мы видим, что при линейном смещении границы растущего кристалла, смещение фронта диффузии пропорционально . Это означает, что за конечное время (назовем его - эффективное время) скорость смещения границы кристалла сравняется со скоростью распространения диффузионного фронта. При этом система стабилизируется и ширина граничного эффекта (т.е. зоны, где концентрации отличны от С₀) будет постоянна.

Обозначим ширину граничного эффекта как L. Тогда, при t > t_e ширина граничного эффекта L(см), определяющаяся разностью координат (4) и (3), будет оставаться постоянной:

(5)

Дифференцируя это уравнение по времени, мы получим время, необходимое для достижения максимальной ширины граничного эффекта:

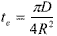(6)

Подставляя (6) в выражение (5), получим:

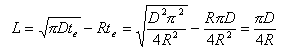(7)

Уравнение (7) показывает, что ширина граничного слоя зависит от валового коэффициента диффузии и от скорости роста кристалла и не зависит от концентраций компонентов (если пренебречь зависимостью коэффициента диффузии от концентрации).

Эти выводы могут быть перенесены на многокомпонентную систему. При этом, учитывая уравнение масс-баланса, которое связывает концентрации всех компонентов, ширина граничного слоя будет зависеть от максимального (или валового) коэффициента диффузии для петрогенных компонентов.

Оценим возможность достижения условий псевдостационарного роста в проведенных экспериментах. Если принять для гаплогранитной системы валовый коэффициент диффузии 10^-11см²/сек [3] и скорость роста 5.55*10^-8 см/сек (2мкм/час - замеренная скорость роста кристаллов во время эксперимента), то ширина стационарного граничного слоя будет составлять 1.41 см, а время, необходимое для достижения стационарного режима роста 2.5*10⁴ сек (т.е. почти 7 часов).

Для базальтовой системы сделать такую оценку сложнее, поскольку неизвестна реальная скорость роста минералов. Принимая коэффициент диффузии 5*10^-9 [3], а скорость роста 3.33*10^-9 см²/сек (12 мкм/час по [5]) мы получим максимальную ширину граничного слоя 12 см за время 2.3*10⁴ сек.

Ни в первом, ни во втором случае таких условий стационарного роста не достигалось, поскольку в экспериментах по росту щелочных полевых шпатов диаметр ампулы составлял 5 мм, а максимальные размеры использовавшихся расплавных включений около 150 мкм. К тому же, выдержка расплавных включений в муфеле (5-10 мин) мала по отношению к рассчитанному времени. Следовательно, полученные профили соответствуют какому-то промежуточному состоянию граничного слоя.

Однако, амплитуда колебаний концентраций компонентов по мере удаления от границы с кристаллом быстро затухает, постепенно приближаясь к валовой концентрации компонента в расплаве. Учитывая значительную относительную ошибку зондовых методов анализа, мы можем пренебречь той частью диффузионного профиля, который незначимо отличается от валовых концентраций расплава.