<< 3.4 Гравитационное поле планеты
| Оглавление |
4.2 Фигуры равновесия >>
Разделы
Термин тяжесть (по-английски gravity) указывает на то, что пробное тело и опора
взаимодействуют. Первое давит на опору, второе дает отклик в виде реакции
опоры. Эти две силы
разной физической природы. Первая имеет гравитационное происхождение, а
вторая -- электромагнитное (упругая сила). Если бы тело находилось в покое,
то обе силы были бы равны и противоположны по направлению. Однако, любое
тело неподвижное относительно поверхности Земли, движется с ускорением, так как совершает вместе с Землей суточное
вращение. По этой причине сумма сил, действующих на тело, не равна нулю.
Результирующая направлена в сторону оси вращения и равна
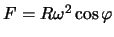 , где , где 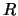 -- радиус Земли в сферическом приближении, -- радиус Земли в сферическом приближении,
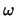 -- угловая скорость вращения, -- угловая скорость вращения, 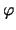 -- геоцентрическая
широта пробного тела. -- геоцентрическая
широта пробного тела.
В теоретической механике широко используется принцип Даламбера : задачи
динамики можно заменить задачами статики, если ввести в рассмотрения силы
инерции -- силы равные и противоположно направленные тем силам, которые
создают ускорение системе отсчета. В частности, если пробное тело неподвижно
на поверхности Земли, то к силе притяжения нужно добавить с обратным знаком
ту силу, которая сообщает пробному телу центростремительное ускорение. Эта сила обычно называется
центробежной. Подчеркнем, что никакой физической природы центробежная сила не имеет. Она
вводится лишь для того, чтобы все задачи механики во вращающейся системе
координат решать, не принимая во внимание неинерциальность системы отсчета,
связанной с вращающейся поверхностью Земли.
Результирующая сил тяготения и центробежной силы получила название силы тяжести. Этот
термин в физике и геофизике имеет разное толкование. В физике под силой
тяжести понимается та сила, с которой тело, обладающее массой 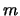 притягивается
к Земле. Если тело освободить от всех связей, то оно будет падать свободно с
ускорением притягивается
к Земле. Если тело освободить от всех связей, то оно будет падать свободно с
ускорением 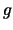 . Тогда сила тяжести, сообщающая телу ускорение свободного
падения, равна . Тогда сила тяжести, сообщающая телу ускорение свободного
падения, равна 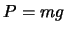 . Эта силы не может служить характеристикой
гравитационного поля, так как зависит от массы пробного тела. Для того,
чтобы силу тяжести превратить в характеристику поля, необходимо пробное тело
сделать стандартным, в геофизике обычно берут массу пробного тела равную
единице. Другими словами, вместо силы тяжести для характеристики поля
используют удельную силу тяжести, то есть силу, отнесенную к единице массы. . Эта силы не может служить характеристикой
гравитационного поля, так как зависит от массы пробного тела. Для того,
чтобы силу тяжести превратить в характеристику поля, необходимо пробное тело
сделать стандартным, в геофизике обычно берут массу пробного тела равную
единице. Другими словами, вместо силы тяжести для характеристики поля
используют удельную силу тяжести, то есть силу, отнесенную к единице массы.
В качестве единицы измерения удельной силы тяжести берут
не Ньютоны на килограмм, а миллигалы, единица,
введенная Вихертом, и широко применяющаяся в геофизике. По размерности,
удельная сила тяжести совпадает с ускорением. Единица измерения 1 Гал равна
ускорению 1 см/с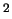 , 1 мГал соответствует ускорению
10 мкм/с , 1 мГал соответствует ускорению
10 мкм/с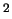 . С повышением
точности, уменьшаются и единицы измерения. В настоящее время существуют
приборы, в которых изменение удельной силы тяжести измеряют в
микрогалах (мкГал) и даже в
наногалах. . С повышением
точности, уменьшаются и единицы измерения. В настоящее время существуют
приборы, в которых изменение удельной силы тяжести измеряют в
микрогалах (мкГал) и даже в
наногалах.
Нужно сказать, что в русской литературе вместо длинного термина удельная сила тяжести чаще
употребляется просто сила тяжести, по умолчанию предполагается, что масса пробного тела
равна единице. Хотя в некоторых статьях, посвященных
гравиметрическим вопросам, вместо термина сила тяжести применяют и ускорение свободного падения, и ускорение силы тяжести. В англоязычной
литературе силу тяжести в нашем понимании называют просто gravity (тяжесть) или на
немецком языке -- schwehre, что тоже обозначает тяжесть. Мы будем придерживаться, в
основном наших русских традиций, хотя иногда вместо силы тяжести будем
говорить просто тяжесть( см. заголовок настоящего раздела).
Потенциал или силовая функция для силы тяжести состоит из двух частей.
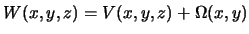 |
(4.1) |
Здесь, снова, декартова система координат выбрана традиционно: ось Oz
совпадает с осью вращения планеты, две другие оси лежат в экваториальной
плоскости.
Гравитационный потенциал (силовую функцию для сил притяжения) 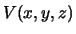 мы
рассмотрели в предыдущих разделах. Остается определить силовую функцию для
центробежной силы ("центробежный потенциал") мы
рассмотрели в предыдущих разделах. Остается определить силовую функцию для
центробежной силы ("центробежный потенциал")
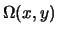 . Поскольку вектор
центробежной силы равен . Поскольку вектор
центробежной силы равен
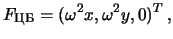 нетрудно догадаться, что
нетрудно догадаться, что
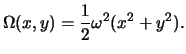
Поверхность
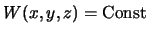 является поверхностью равного потенциала или
эквипотенциальной поверхностью. Сила тяжести равна производной этого потенциала по вдоль
внутренней нормали. Равенство нулю компоненты силы, касательной к
поверхности, говорит о том, что эта поверхность является поверхностью уровня. Меняя значение
постоянной для потенциала, мы получим семейство поверхностей, обладающих
следующими свойствами: является поверхностью равного потенциала или
эквипотенциальной поверхностью. Сила тяжести равна производной этого потенциала по вдоль
внутренней нормали. Равенство нулю компоненты силы, касательной к
поверхности, говорит о том, что эта поверхность является поверхностью уровня. Меняя значение
постоянной для потенциала, мы получим семейство поверхностей, обладающих
следующими свойствами:
--
чем больше значение силы тяжести, тем ближе две соседние уровенные
поверхности,
--
две уровенные поверхности не пересекаются. Если бы они могли пересекаться,
то в точке пересечения существовали бы две нормали, а следовательно и две
силы тяжести, что невозможно.
<< 3.4 Гравитационное поле планеты
| Оглавление |
4.2 Фигуры равновесия >>
|

