Next: 5.4. Идеальное разделение секрета
Up: 5. Математика разделения секрета
Previous: 5.2. Разделение секрета для
Contents: Содержание
5.3. Линейное разделение секрета
Начнем с предложенной А. Шамиром [2]
элегантной схемы разделения секрета
для пороговых структур доступа. Пусть 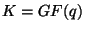 конечное поле из конечное поле из 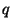 элементов (например,
элементов (например, 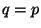 - простое число
и - простое число
и 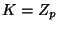 ) и ) и 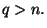 Сопоставим участникам Сопоставим участникам  различных ненулевых
элементов поля различных ненулевых
элементов поля
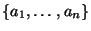 и положим и положим 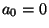 . При
распределении секрета . При
распределении секрета 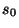 дилер СРС
генерирует дилер СРС
генерирует 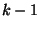 независимых равномерно распределенных на независимых равномерно распределенных на
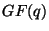 случайных величин случайных величин 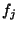 ( (
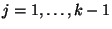 )
и посылает )
и посылает 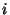 -му участнику
( -му участнику
(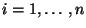 ) ``его'' значение ) ``его'' значение 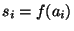 многочлена многочлена
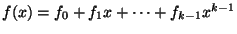 , где , где 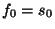 .
Поскольку любой многочлен степени .
Поскольку любой многочлен степени 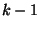 однозначно восстанавливается по его значениям в произвольных
однозначно восстанавливается по его значениям в произвольных  точках
(например, по интерполяционной формуле Лагранжа), то
любые точках
(например, по интерполяционной формуле Лагранжа), то
любые  участников вместе могут восстановить многочлен участников вместе могут восстановить многочлен 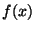 и,
следовательно, найти значение секрета как и,
следовательно, найти значение секрета как 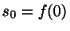 . По этой же причине для
любых . По этой же причине для
любых 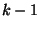 участников, любых полученных ими значений
проекций участников, любых полученных ими значений
проекций 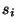 и любого значения секрета и любого значения секрета 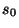 существует ровно один
``соответствующий'' им многочлен, т.е.
такой, что существует ровно один
``соответствующий'' им многочлен, т.е.
такой, что 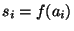 и и 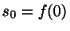 .
Следовательно, эта схема является совершенной в соответствии
с определением 2.
``Линейность'' данной схемы становится ясна, если записать ``разделение
секрета'' в векторно-матричном виде: .
Следовательно, эта схема является совершенной в соответствии
с определением 2.
``Линейность'' данной схемы становится ясна, если записать ``разделение
секрета'' в векторно-матричном виде:
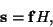 |
(3) |
где
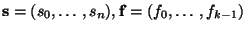 , , 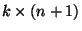 -матрица -матрица
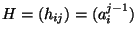 и и 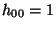 .
Заметим, что любые .
Заметим, что любые  столбцов этой
матрицы линейно независимы,
а максимально возможное число столбцов матрицы столбцов этой
матрицы линейно независимы,
а максимально возможное число столбцов матрицы 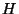 равно равно
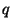 , и чтобы добиться обещанного в разделе 1 значения , и чтобы добиться обещанного в разделе 1 значения 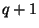 надо
добавить столбец, соответствующий точке ``бесконечность''. надо
добавить столбец, соответствующий точке ``бесконечность''.
Упражнение. Придумайте сами, как это сделать.
Возьмем в (3) в качестве 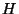 произвольную произвольную
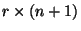 -матрицу с элементами из поля -матрицу с элементами из поля 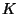 . Получаемую СРС будем называть одномерной
линейной СРС. Она является совершенной комбинаторной СРС со структурой доступа . Получаемую СРС будем называть одномерной
линейной СРС. Она является совершенной комбинаторной СРС со структурой доступа 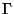 ,
состоящей из множеств ,
состоящей из множеств  таких, что вектор таких, что вектор 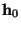 представим в виде
линейной комбинации векторов представим в виде
линейной комбинации векторов
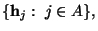 где
где 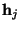 это это 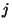 -ый столбец матрицы -ый столбец матрицы 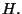 Строками матрицы
Строками матрицы 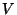 , соответствующей данной СРС являются, как видно из
(3),
линейные комбинации строк матрицы , соответствующей данной СРС являются, как видно из
(3),
линейные комбинации строк матрицы 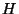 . Перепишем
(3)
в следующем виде . Перепишем
(3)
в следующем виде
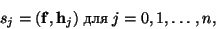
где
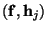 -
скалярное произведение векторов -
скалярное произведение векторов
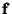 и и 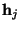 . Если . Если 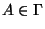 ,
т.е. если ,
т.е. если
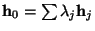 , то , то
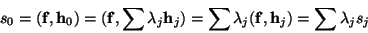
и, следовательно, значение секрета однозначно находится по его ``проекциям''.
Рассмотрим теперь случай, когда вектор 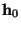 не представим в виде
линейной комбинации векторов не представим в виде
линейной комбинации векторов
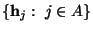 . Нам нужно показать,
что в этом случае для любых заданных значений координат из множества . Нам нужно показать,
что в этом случае для любых заданных значений координат из множества  число
строк матрицы число
строк матрицы 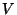 с данным значением нулевой координаты не зависит от этого
значения. В этом нетрудно убедиться, рассмотрев (3) как систему линейных
уравнений относительно неизвестных с данным значением нулевой координаты не зависит от этого
значения. В этом нетрудно убедиться, рассмотрев (3) как систему линейных
уравнений относительно неизвестных 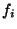 и воспользовавшись тем, что система
совместна тогда и только тогда, когда ранг матрицы коэффициентов
равен рангу расширенной матрицы, а число решений у совместных систем
одинаково и равно числу решений однородной системы. и воспользовавшись тем, что система
совместна тогда и только тогда, когда ранг матрицы коэффициентов
равен рангу расширенной матрицы, а число решений у совместных систем
одинаково и равно числу решений однородной системы.
Указание. Рассмотрите две системы:
без ``нулевого'' уравнения (т.е. со
свободным членом) и с ним. Так как вектор 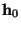 не
представим в виде
линейной комбинации векторов не
представим в виде
линейной комбинации векторов
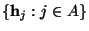 , то
ранг матрицы коэффициентов
второй системы на 1 больше ранга матрицы коэффициентов первой системы.
Отсюда немедленно следует, что если первая система совместна, то совместна и
вторая при любом , то
ранг матрицы коэффициентов
второй системы на 1 больше ранга матрицы коэффициентов первой системы.
Отсюда немедленно следует, что если первая система совместна, то совместна и
вторая при любом 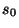 . .
Эта конструкция подводит нас к определению общей линейной СРС. Пусть секрет и
его ``проекции''
представляются как конечномерные векторы
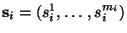 и
генерируются по формуле и
генерируются по формуле
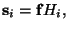 где где
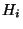 - некоторые - некоторые 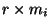 -матрицы. Сопоставим каждой матрице -матрицы. Сопоставим каждой матрице 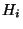 линейное пространство
линейное пространство 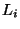 ее столбцов (т.е. состоящее из всех линейных
комбинаций вектор-столбцов матрицы ее столбцов (т.е. состоящее из всех линейных
комбинаций вектор-столбцов матрицы 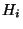 ). Несложные рассуждения, аналогичные
приведенным выше для одномерного случая (все ). Несложные рассуждения, аналогичные
приведенным выше для одномерного случая (все 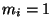 ), показывают, что данная
конструкция дает совершенную СРС тогда и только тогда, когда
семейство линейных подпространств ), показывают, что данная
конструкция дает совершенную СРС тогда и только тогда, когда
семейство линейных подпространств
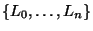 конечномерного векторного пространства
конечномерного векторного пространства 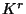 удовлетворяет упомянутому во введении свойству
``все или ничего''. При этом множество удовлетворяет упомянутому во введении свойству
``все или ничего''. При этом множество  является разрешенным ( является разрешенным (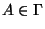 ),
если и только если линейная оболочка подпространств ),
если и только если линейная оболочка подпространств
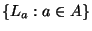 содержит
подпространство содержит
подпространство 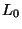 целиком. С другой стороны, множество целиком. С другой стороны, множество  является
неразрешенным ( является
неразрешенным (
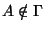 ), если и только если линейная оболочка
подпространств ), если и только если линейная оболочка
подпространств
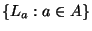 пересекается с подпространством пересекается с подпространством 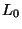 только по вектору
только по вектору 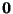 . Отметим, что если
бы для некоторого . Отметим, что если
бы для некоторого  пересечение пересечение
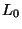 и линейной оболочки и линейной оболочки
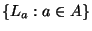 было нетривиальным, то участники было нетривиальным, то участники  не могли бы восстановить секрет однозначно, но
получали бы некоторую информацию о нем, т.е. схема не была бы совершенной. не могли бы восстановить секрет однозначно, но
получали бы некоторую информацию о нем, т.е. схема не была бы совершенной.
Пример 3.
Рассмотрим следующую структуру доступа
для случая четырех участников, задаваемую
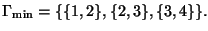 Она известна как
первый построенный пример структуры доступа, для которой
не существует идеальной реализации. Более того, было
доказано, что для любой ее совершенной реализации Она известна как
первый построенный пример структуры доступа, для которой
не существует идеальной реализации. Более того, было
доказано, что для любой ее совершенной реализации
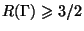 . С другой стороны, непосредственная проверка
показывает, что
выбор матриц . С другой стороны, непосредственная проверка
показывает, что
выбор матриц
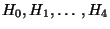 , приведенных в табл. 1,
дает совершенную линейную СРС с , приведенных в табл. 1,
дает совершенную линейную СРС с 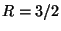 , реализующую эту структуру,
которая, следовательно, является и оптимальной
(наиболее экономной) СРС. , реализующую эту структуру,
которая, следовательно, является и оптимальной
(наиболее экономной) СРС.
Таблица 1.
![\begin{table}%%{Таблица 1.}
{\par\begin{displaymath}
\arraycolsep=2pt
H_0=\lef...
...0\!\\
\!0\!&\!1\!\ \end{array}\right].
\end{displaymath}
\par }
\end{table}](http://images.geo.web.ru/pubd/2001/10/08/0001161235/img1036.gif) |
Next: 5.4. Идеальное разделение секрета
Up: 5. Математика разделения секрета
Previous: 5.2. Разделение секрета для
Contents: Содержание
|

