Громалова Наталья Александровна
Автореферат диссертации на соискание ученой степени кандидата геолого - минералогических наук
|
содержание |
Теоретическое моделирование с использованием атомистических межатомных потенциалов было использовано для описания структурных, упругих и термодинамических свойств хризоберилла, предсказания аналогичных характеристик его изоструктурных аналогов, а также для оценки термодинамической стабильности твердых растворов на основе хризоберилла.
Компьютерное моделирование осуществлялось при помощи программы GULP версии 3.0. Разработанный набор параметров потенциалов в ионно - ковалентном приближении был использован при моделировании структур и свойств бромеллита BeO, хризоберилла и его изоструктурных аналогов: BeСr2O4, а также неизученного до сих пор рентгеновскими методами BeFe2O4.
Рассчитанные параметры элементарной ячейки хризоберилла отличаются от экспериментальных величин не более чем на 1%, а координаты атомов - не более чем на 1,75%. Модуль всестороннего сжатия отличается от экспериментальной величины всего на 7%. Энтропия хризоберилла согласуется с экспериментальными значениями в пределах ±3% в интервале температур от 298 до 1800 К. Рассчитанные параметры элементарной ячейки Cr - аналога хризоберилла отличаются от экспериментальных величин не более чем на 0,5 %. Это дает основание считать рассчитанные структурные, упругие и термодинамические свойства BeCr2O4 и BeFe2O4 достаточно достоверным предсказанием.
Энергетика образования собственных и примесных дефектов в исследуемых соединениях была изучена с помощью известной модели Мотта - Литтлтона. Для хризоберилла и его аналогов наиболее предпочтительными являются бериллиевые пары Френкеля, а для бромеллита - дефекты Шоттки, при этом октаэдрическая позиция более выгодна для вхождения междоузельного Ве, чем тетраэдрическая, что согласуется с ab initio расчетом (Софронов, Горбунова, 2006). Во всех соединениях анионные пары Френкеля являются наиболее энергетически затратными и их образование маловероятно.
Моделирование свойств смешения в системах на основе BeAl2O4
Для расчета свойств смешения твердых растворов в системе BeAl2O4 - BeCr2O4 была выбрана сверхъячейка 4ах2bх2c, число катионов в октаэдрических позициях которой равно 128. Все расчеты проводились для пр.гр. P1. Конфигурация распределений октаэдрических катионов разных сортов в исходной сверхъячейке заданного состава определялась для каждой позиции M1 и M2 по разработанной в (Еремин и др., 2008) методике. Для учета отклонения распределения катионов Cr3+ и Fe3+ по позициям М1 и М2 от статистического было использовано экспериментальное отношение q(CrM2) = x(CrM2)/x(CrM1+CrM2) = 2/3 = 67% из работы (Рабаданов, Дудка, 1998).
Свойства смешения (энтальпия (ΔHсм), энтропия (ΔSсм), объем (ΔV) и модуль сжатия (ΔK)) рассчитывались согласно известным соотношениям (Урусов, 1977). Эти свойства сильно зависят от распределения катионов между позициями M1 и M2 (рис.9). Например, при q(CrM2)=2/3 энтальпия смешения описывается слегка ассиметричной параболой, достигающей своего максимального значения при x(Cr) = 0,57.
Расчеты показали крайне малое отрицательное отклонение объема от аддитивности: наибольшее отклонение ΔV = -0,15 Å3. Такое отклонение, по - видимому, не может быть измерено экспериментально с необходимой точностью. Отклонения модулей всестороннего сжатия от аддитивности также отрицательны для всех составов твердого раствора. Величины отклонений не превышают 3,5 ГПа, что, вероятно, с трудом может быть подвергнуто экспериментальной проверке.
Для получения значений колебательной энтропии смешения ΔSкол были проведены вычисления колебательных спектров для всех изучаемых составов при различных температурах в диапазоне от 300 до 1900 К. Расчеты показали, что значения конфигурационной энтропии Sконф являются для этой системы определяющими, а величины ΔSкол значительно меньше. Величины ΔSкол практически постоянны для каждого состава х (с точностью до 3 - 4%) во всем исследуемом интервале температур, что дает основание предполагать отсутствие зависимости ΔHсм от T.
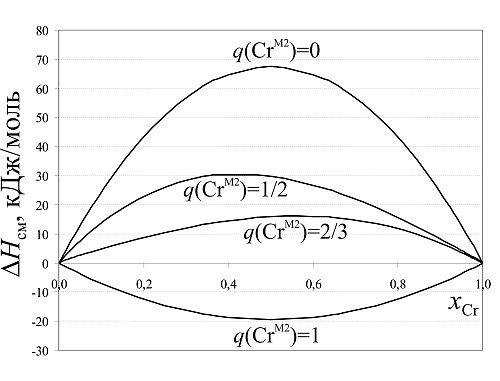 |
| Рис. 9. Энтальпия смешения твердого раствора BeAl2O4 - BeCr2O4 для различных вариантов распределения Cr3+ и Al3+ по позициям M1 и M2. |
Вычисленные значения ΔHсм и ΔSсм позволили построить зависимости свободной энергии Гиббса ΔGсм от состава бинарных твердых растворов при различных температурах в диапазоне от 300 до 2300К (рис.10). Видно, что ΔGсм сильно зависит от q(CrM2). На основе графических построений были найдены составы сосуществующих твердых растворов, отвечающих минимумам на кривых ΔG(x) при T ~ 1000 K (рис. 11). Положение сольвуса сильно зависит от распределения катионов по октаэдрическим позициям: статистическое распределение (q(CrM2) = 1/2) приводит к более узким областям существующих твердых растворов, чем частично упорядоченное (q(CrM2) = 2/3). Для последних критическая температура оценена как 2300±20 К при xСr = 0,45, т.е. несколько превышает температуру плавления хризоберилла, следовательно, купол сольвуса в действительности не замыкается. Более того, согласно данным Гусарова, Семина (1992) при температуре 2016 К хризоберилл α - BeAl2O4 претерпевает фазовый переход в β - BeAl2O4 с тетраэдрической координацией Al.
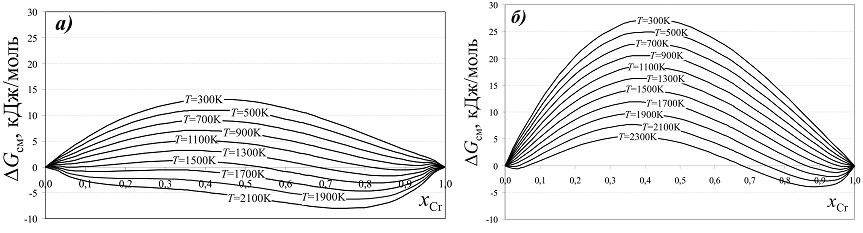 |
| Рис.10. Кривые ΔGсм в системе BeAl2O4 - BeCr2O4: а) при q(CrM2) = 2/3; б) при q(CrM2) = 1/2. |
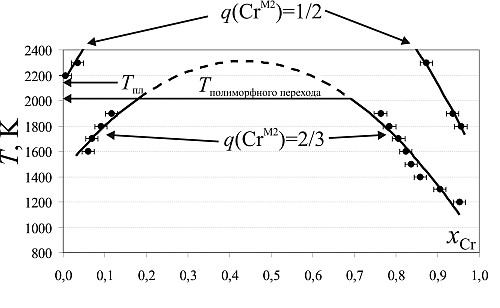 |
| Рис. 11. Кривые сольвуса в системе BeAl2O4 - BeCr2O4 для статистического (q(CrM2) = 1/2) и частично упорядоченного (q(CrM2) = 2/3) распределения катионов по октаэдрическим позициям. Пунктирными линиями показано положение критической точки. Вертикальные и горизонтальные области ошибок соответствуют точности графического построения. |
|

