Капустин Владимир Викторович
Автореферат диссертации на соискание ученой степени кандидата физико-математических наук
|
содержание |
1. Физические модели сред, используемые при описании акустических полей в геотехнических и строительных конструкциях.
Для получения информации о строении и свойствах исследуемых конструкций могут быть использованы проходящие и отраженные волны всех типов - продольные, поперечные и поверхностные. В то же время, как показано в работе, большой интерес для исследования протяженных конструкций представляют волны "направляемого типа": поверхностные, гидроволны, волны, распространяющиеся в волноводах (стержни, пластины, оболочки). У данного типа волн есть целый ряд полезных свойств, дающих им преимущество по сравнению с другими волнами - высокая интенсивность, низкое затухание в направлении распространения, низкая скорость, наличие сдвиговой компоненты. Очевидно, что акустическое поле, возбуждаемое в конструкции, находящейся в грунтовом массиве, зависит также от упругих свойств грунта. Поэтому построенные математические модели учитывают данное обстоятельство. Расчет акустического поля производится путем численного решения уравнения движения Mu''+Cu'+Ku=F, где u- вектор смещения, M-матрица масс, С - матрица затухания, К - матрица деформации, F - вектор нагрузки, с соответствующими каждой модели начальными
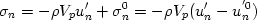
и граничными условиями.
Так как вычисления производятся в ограниченном объеме среды, для учета искажающего влияния границ расчетной области на них вводятся специальные условия:
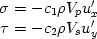
где С1 и С2 -коэффициенты ослабления.
Для моделей, имеющих вертикальные границы, граничные условия на них могут задаваться по нежесткому типу:
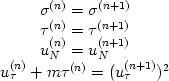
Для описания поля в сваях используются осесимметричные модели, для ленточных, плитных фундаментов, стен в грунте и др. - плоские модели. Численное решение уравнения движения выполняется методом конечных элементов, с неравномерным заданием конечно-разностной сетки. Для проведения вычислений применялась схема Ньюмарка с использованием способа неявного интегрирования по времени:
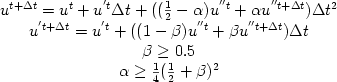
При решении прямых задач с использованием механического (ударного) возбуждения акустического поля нагрузка (F) задавалась в виде полупериода синусоиды. Используемая расчетная схема допускает также и другие способы задания нагрузки.
К настоящему времени получены решения задач методом конечных элементов для следующих моделей:
расчет волнового поля в цилиндрической свае, находящейся в слоистом грунте;
расчет волнового поля для двух свай, находящихся на едином жестком основании, при возбуждении вертикальной силой на поверхности одной сваи и регистрации сигнала на другой;
расчет волнового поля, при возбуждении его вертикальной силой на поверхности стены в грунте или ленточного фундамента;
расчет волнового поля, возбуждаемого вертикальной силой на поверхности фундаментной плиты, лежащей на грунтовом основании;
расчет волнового поля, возбуждаемого вертикальной силой на поверхности слоистого полупространства, содержащего локальные неоднородности;
расчет волнового поля в водонаполненной скважине для источника типа направленной силы.
2. Прямые акустические задачи для используемых моделей сред. Решение и анализ.
К настоящему времени имеется опыт применения сейсмических и акустических методов при исследовании существующих и строящихся фундаментов, в частности, сплошных (фундаментные плиты), свайных и ленточных фундаментов.
1. Фундаментные плиты.
Для построения методики наблюдения и интерпретации материла в задачах связанных с исследованием фундаментных плит построено решение методом конечных элементов для расчета волнового поля, возбуждаемого вертикальной силой на поверхности ограниченной фундаментной плиты, лежащей на грунтовом основании. Как показывают результаты моделирования, при ухудшении контактных условий происходит подъем интенсивности амплитудного спектра сигнала в полосе толщинного резонанса. Частным случаем данной задачи является случай математического моделирования волнового поля поверхностных волн, возбуждаемого вертикальной силой в слоистом полупространстве, содержащим локальные неоднородности. Особенно интересен для практических приложений случай, когда локальными неоднородностями являются пустоты. Как показали результаты математического моделирования, на участках расположения пустот наблюдается возрастание спектральных амплитуд поверхностных волн. Полученные результаты могут использоваться при интерпретации данных метода спектрального анализа поверхностных волн (SASW).
2. Свайные фундаменты.
Для исследования свайных фундаментов используются, в основном, поверхностные акустические технологии. В работе проанализированы результаты математического моделирования и натурных измерений.
Показано, что:
1. Динамические и кинематические характеристики продольных волн в свае существенно зависят от свойств вмещающего грунта;
2. Фазовые характеристики отраженного импульса зависят от свойств основания, на которые опирается свая (вплоть до инверсии);
3. В зависимости от акустических свойств вмещающих грунтов происходит либо интенсивное излучение энергии упругих волн из сваи, либо акустическая энергия аккумулируется внутри сваи.
Наличие явлений геометрической дисперсии и отражений на участках пересечения сваей контрастных слоев в ряде случаев могут привести к ошибкам при интерпретации натурных наблюдений. Избежать этого позволяет использование результатов математического моделирования.
Построенная математическая модель распространения акустических волн между двумя сваями, опирающимися на жесткое основание, позволяет проводить качественную оценку несущей способности свай.
3. Ленточные фундаменты.
Для ленточного фундамента была использована математическая модель возбуждения акустического поля вертикальной силой на поверхности линейно-упругой призмы, находящейся в слоистом полупространстве. Решение данной задачи может быть получено как для точек, находящихся внутри фундамента, так и для точек, находящихся в грунтовом массиве. Последнее обстоятельство позволило рассчитать коэффициент передачи для выбранной модели фундамента.
3. Описание геоэлектрической модели в околоскважинном пространстве при использовании изолированных электромагнитных антенн.
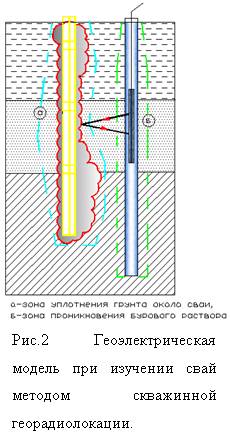
Особенностью метода скважинной георадиолокации является различие геоэлектрических моделей среды по сравнению с применяемой при подповерхностных исследованиях. Во-первых, при проведении исследований необходимо учитывать изменение скорости распространения радиоволн вдоль профиля наблюдений (как правило, уменьшение скорости с глубиной), во-вторых, приходится иметь дело с изучением отражений от границы со средой с меньшей диэлектрической проницаемостью, в-третьих, наличие в разрезе как субгоризонтальных, так и субвертикальных границ (литологические границы).
Возможности скважинной радиолокации для обследования свайных конструкций были изучены при проведении натурных наблюдений. Изучались два типа свай: армированные стальным каркасом и неармированные. Решение задачи определения геометрии поверхности неармированной сваи получено с приемлемой для практического применения точностью для случая нахождения сваи в кусочно-однородной среде при минимальном количестве промежуточных границ (Рис. 2).
4. Описание геоэлектрической модели при использовании подповерхностной радиолокации для изучения фундаментных и геотехнических конструкций.
При использовании электромагнитных волн для изучения строительных и геотехнических конструкций могут применяться те же приемы, что и при использовании акустических методов. Система уравнений Максвелла, описывающая поле электрической антенны с соответствующими граничными и начальными условиями, для ряда моделей может быть решена численными методами. Для исследования фундаментных конструкций, в ряде случаев, может быть предложено использование направляемых волн. У данного типа волн имеется одно универсальное свойство: поле направляемой волны обязательно имеет поперечные электрическую 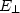 и и 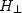 магнитные составляющие, лежащие в плоскости перпендикулярной оси распространения - Х. Это является необходимым условием существования продольной компоненты вектора Умова-Пойнтинга Px =[E,H], определяющей передачу энергии вдоль направляющей системы. Для электрической антенны, находящейся на поверхности слабопроводящего полупространства, при наличии под поверхностью субвертикальных границ могут создаваться условия для образования "направляемых волн", при соблюдении соотношения для критического угла падения вытекающего из закона Снеллиуса: магнитные составляющие, лежащие в плоскости перпендикулярной оси распространения - Х. Это является необходимым условием существования продольной компоненты вектора Умова-Пойнтинга Px =[E,H], определяющей передачу энергии вдоль направляющей системы. Для электрической антенны, находящейся на поверхности слабопроводящего полупространства, при наличии под поверхностью субвертикальных границ могут создаваться условия для образования "направляемых волн", при соблюдении соотношения для критического угла падения вытекающего из закона Снеллиуса:
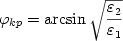 при условии, что при условии, что 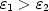
Полезной особенностью направляемых волн является их меньшее затухание, по сравнению с волнами, распространяющимися в безграничной среде. Примерами физических моделей могут служить сваи и ленточные фундаменты, верхняя граница которых находится близко от дневной поверхности. Бетонные армированные сваи могут служить грубой моделью коаксиальной линии.
|

