Аппаратурно-методический комплекс для геофизических исследований процессов фильтрации на пресноводных водоемах

Глава 2. Метод естественного электрического поля на акваториях.

В начале главы представлен краткий обзор современных методов решения прямой задачи для метода ЕП. Анализ показал, что имеет место явный дефицит решения прямой задачи метода ЕП на акваториях, связанной с явлениями фильтрации через дно и борта водоема, в то время как практика таких наблюдений, хотя и эпизодически, но имеет место. Представляется обоснованным, что геоэлектрическая модель водоема (водный объем и окружающие отложения), на первом этапе своей разработки не должна быть излишне сложной, что позволяет исследовать поле не только во всем объеме среды, но и получать асимптотические оценки для более сложных случаев строения среды, а также определять порядки величин.

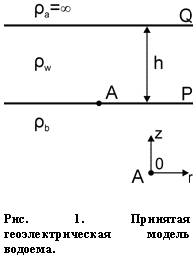
Для выяснения основных количественных закономерностей в рамках исследования был сделан выбор на одномерной двухслойной модели водоема, представленной на рис. 1. Модель состоит из нижнего полупространства донных отложений с УЭС ρ_b, залегающего выше горизонтального слоя воды мощности h с УЭС ρ_w и воздушного верхнего полупространства с УЭС ρ_a = ∞. Элементы модели разделены двумя горизонтальными и параллельными границами: дно P и граница вода - воздух Q. Все элементы модели однородные и изотропные по электрическим свойствам. Задача ставится следующим образом: найти распределение потенциала всюду в водном слое от точечного источника тока A силой I, расположенного на границе P.

Перед записью решения необходимо уточнить физическую природу источника тока A. В рамках модели предполагается, что в непосредственной близости к водному слою в точке A расположен лишь одна из пары сопряженных областей вхождения/выхождения жидкости в объем породы, а расположение дополняющей области неизвестно, но полагается достаточно удаленным, для того чтобы считать точку А единичным точечным источником тока, стекающего во все проводящее пространство. Поток жидкости через объем горной породы полагается установившимся, а скорость потока и соответствующее электрическое поле стационарным. Таким образом, в точке A рассматривается стационарный точечный механо-электрический генератор, который преобразует механическую энергию жидкости, фильтрующейся через объем горной породы, в электрический ток, стекающий в проводящую среду.

Решение для потенциала электрического поля в слое воды получено в аналитическом виде методом решения уравнения Лапласа и может быть представлено следующим образом:

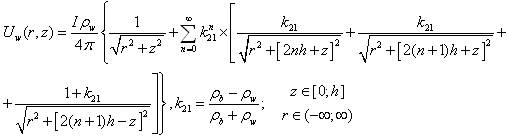(1)

В целях увеличения производи тельности алгоритма численного моделирования фильтрационного поля, под эффективным источником тока понимается некая двумерная квадратная область поверхности дна водоема, на которой расположены выходы капилляров зоны фильтрации. При формировании такой модели, были приняты как минимум три существенных допущения о структуре водопроницаемого порового пространства отложений, расположенных ниже дна водоема. Во-первых, все капилляры зоны фильтрации полагаются цилиндрическими и вертикальными (оси капилляров пересекаются под прямым углом с поверхностью дна водоема P) с постоянным радиусом по их длине. Во-вторых, предполагается, что капилляры распределены равномерно в объеме породы с некоторой площадной пористостью (отношение суммарной площади сечений капилляров к площади квадратной площадки). В-третьих, считается, что мощность отложений под дном достаточно велика, а, следовательно, и обратные выходы капилляров расположены на достаточной глубине, чтобы их потенциал не учитывать в расчетах. Сделанные предположения позволяют воспользоваться моделью Смолуховского - Гельмгольца для тока проводимости, стекающего с концов капилляров зоны фильтрации.

Линейность решения (1) задачи позволяет формировать на дне водоема зоны фильтрации произвольной формы путем аппроксимации их геометрии набором эффективных источников тока. В результате всюду в водном слое можно вычислить потенциал фильтрационного поля от всех эффективных источников тока образующих зоны фильтрации. После приведения выражения (1) к прямоугольной системе координат выражение для суммарного потенциала можно записать как:

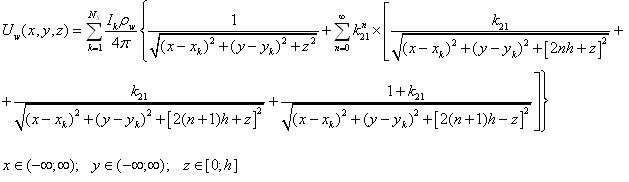(2)

где N_S - общее количество эффективных источников входящих в состав всех зон фильтрации; I_k, x_k, y_k - ток проводимости и координаты k-ого эффективного источника соответственно.

На основе выражения (2) численными методами исследованы количественные закономерности распределения потенциала ЕЭП в водном слое для принятой модели водоема. Одна из выявленных особенностей состоит в том, что максимум аномалии потенциала от зоны фильтрации падает с увеличением глубины водоема медленнее, чем растет <ширина> аномалии при тех же условиях. С практической точки зрения такое поведения аномальной части потенциала ЕЭП выгодно с двух сторон. Во-первых, малая скорость уменьшения максимума аномалии с увеличением глубины водоема, повышает отношение сигнал/шум и увеличивает вероятность выявления аномалии в процессе полевых наблюдений. Во-вторых, большая степень <расширения> аномалии с увеличением глубины водоема позволяет её обнаружить на значительном расстоянии от фактического источника. Для типичных значений УЭС дна (50 - 100 Ом^.м), при прочих равных условиях, максимум аномалии ЕЭП от источника фильтрации линейно растет с контрастом сопротивлений в диапазоне ρ_w/ρ_b > 10 и нелинейно падает до нуля при ρ_w/ρ_b < 10.

Таким образом, получен инструмент для нахождения количественных характеристик ЕЭП фильтрационной природы в водном слое в непосредственной близости к дневной поверхности. Появилась возможность оценивать порядки изучаемых величин и разрабатывать эффективные методики натурных наблюдений по методу ЕП в водном варианте.