|
Ю. И. Галушкин, Е. П. Дубинин,
А. А. Свешников, С. А. Ушаков
Московский государственный
университет им. М. В. Ломоносова, Музей
землеведения
Опубликовано:"Российский журнал
наук о Земле" том 2, N4, Декабрь 2000 |
Содержание |
Н. Слип [Sleep, 1974, 1975] первым анализировал
распределение теплового потока и температур в
осевой зоне СОХ. Он решал стационарное уравнение
теплопроводности (1) c A(x,z)=0 в
прямоугольной области x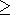 0, 0 0, 0 z z H со стандартными
граничными условиями: T=0 на поверхности
области счета (z=0), T=TH в ее
основании (z=H) и H со стандартными
граничными условиями: T=0 на поверхности
области счета (z=0), T=TH в ее
основании (z=H) и  T/ T/ x=0
при x= x=0
при x=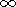 . На оси x=0
задавался тепловой поток: . На оси x=0
задавался тепловой поток:
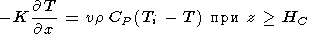 |
(5) |
где HC - толщина коры, и
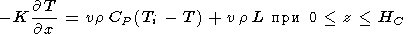 |
(6) |
в пределах коры. Здесь L = 90 кал/г - скрытая
теплота плавления базальта. Температура пород интрузивной зоны Ti росла с
глубиной по кусочно-линейному закону с
градиентом dTi/dz=3 oС/км в
пределах коры (0 z z HC), 1oС/км
- в пределах зоны сегрегации (HC HC), 1oС/км
- в пределах зоны сегрегации (HC z z HS), где HS =
33 км и 0,3oС/км - в пределах адиабатической
зоны в мантии (HS HS), где HS =
33 км и 0,3oС/км - в пределах адиабатической
зоны в мантии (HS z z H),
где (dT/dz)ad=0,3 oС/км -
адиабатический градиент температуры в мантии.
(Из других параметров, используемых в модели: K
=0,006 кал/см сoC, rCp=0,91 кал/см3
oС, TH = 1290oС, H = 100 км.) H),
где (dT/dz)ad=0,3 oС/км -
адиабатический градиент температуры в мантии.
(Из других параметров, используемых в модели: K
=0,006 кал/см сoC, rCp=0,91 кал/см3
oС, TH = 1290oС, H = 100 км.)
Решение получалось разложением искомого
распределения температуры в ряды Фурье. Вдали от
оси ( x = 0), где горизонтальные градиенты
температур были пренебрежимы, глубины изотерм
были близки к полученным в моделях [McKenzie, 1967] и [Oldenburg, 1975].
В то же время учет эффекта скрытой теплоты
плавления позволил Н. Слипу более корректно
описать высокотемпературный режим приосевой
области океанической литосферы и даже
приблизиться к имитации теплового режима подосевой магматической камеры [Sleep,
1975].
И все же в ряде деталей модель нуждалась в
усовершенствовании. Прежде всего, это касалось
условий на оси рифта (5) и (6). Они предполагают
отличие производной  T/ T/ x
от нуля на оси x=0, что отражается в резком
заглублении изотерм у оси хребта с крутизной их
наклона, растущим с увеличением скорости
спрединга v [Sleep, 1975]. Это
противоречит наблюдениям в СОХ, согласно которым
как изотермы, так и кровля магматического очага,
в осевой области почти горизонтальны, что
соответствует условию x
от нуля на оси x=0, что отражается в резком
заглублении изотерм у оси хребта с крутизной их
наклона, растущим с увеличением скорости
спрединга v [Sleep, 1975]. Это
противоречит наблюдениям в СОХ, согласно которым
как изотермы, так и кровля магматического очага,
в осевой области почти горизонтальны, что
соответствует условию  T/ T/ x=0.
Можно отметить также, что высокотемпературные
изотермы в модели, и в том числе изотерма,
фиксирующая кровлю очага, располагаются заметно
ближе к поверхности дна, чем это следует из
сейсмических наблюдений. Выделение скрытой
теплоты плавления в модели [Sleep, 1975], локализовано в коре в
пределах узкой зоны на оси спрединга, причем
предполагается выделение полного объема теплоты
плавления независимо от степени плавления ее
вещества (температура ликвидуса пород коры TL
вообще не участвует в вычислениях температуры). В
реальной ситуации скрытая теплота
распределяется по широкой области затвердевания
пород, включающей объем и кровлю и края
магматического очага и ее величина сильно
зависит от локальной степени плавления вещества
коры. x=0.
Можно отметить также, что высокотемпературные
изотермы в модели, и в том числе изотерма,
фиксирующая кровлю очага, располагаются заметно
ближе к поверхности дна, чем это следует из
сейсмических наблюдений. Выделение скрытой
теплоты плавления в модели [Sleep, 1975], локализовано в коре в
пределах узкой зоны на оси спрединга, причем
предполагается выделение полного объема теплоты
плавления независимо от степени плавления ее
вещества (температура ликвидуса пород коры TL
вообще не участвует в вычислениях температуры). В
реальной ситуации скрытая теплота
распределяется по широкой области затвердевания
пород, включающей объем и кровлю и края
магматического очага и ее величина сильно
зависит от локальной степени плавления вещества
коры.
|

