




Вперед: 15. Основные понятия теории доказательств с нулевым разглашением
Вверх: 14. Односторонние функции и псевдослучайные генераторы
Назад: 14.1.5 Функции с секретом
Содержание
Предметный указатель
14.2 Псевдослучайные генераторы
Псевдослучайные генераторы в криптографической практике
используются, в основном, при построении потоковых
криптосистем с секретным ключом (в другой терминологии --
шифраторов гаммирования), которые в банковских приложениях
применяются редко. Но, тем не менее, мы включили в
настоящие методические материалы некоторые начальные
сведения по теории псевдослучайных генераторов, поскольку
практически для любой криптографической схемы требуется
генератор псевдослучайных величин. А одна из задач теории
псевдослучайных генераторов -- объяснить, что такое
криптографически надежный источник псевдослучайности.
В работах по теоретической криптографии термин
"псевдослучайный генератор" используется как сокращение
для термина "надежный (стойкий) генератор псевдослучайных
последовательностей". Само понятие возникло как результат
многочисленных попыток определить те требования, которым
должна удовлетворять псевдослучайная последовательность,
чтобы ее можно было признать "достаточно похожей" на
случайную. Такие требования формализуются в виде так
называемых статистических тестов. Наиболее популярные из
них -- большая длина периода, близкое к равномерному
распределение  -грамм (это означает, что частота
появления всех возможных -грамм (это означает, что частота
появления всех возможных  -битовых подстрок должна быть
приблизительно одинаковой) и т. д. Определение
псевдослучайного генератора заменяет этот потенциально
бесконечный набор требований одним: последовательность
является псевдослучайной, если она проходит все
статистические тесты, которые могут быть выполнены за
полиномиальное время. Иными словами, последовательность
называется псевдослучайной, если любой полиномиальный
алгоритм может отличить ее от случайной последовательности
лишь с пренебрежимо малой вероятностью. -битовых подстрок должна быть
приблизительно одинаковой) и т. д. Определение
псевдослучайного генератора заменяет этот потенциально
бесконечный набор требований одним: последовательность
является псевдослучайной, если она проходит все
статистические тесты, которые могут быть выполнены за
полиномиальное время. Иными словами, последовательность
называется псевдослучайной, если любой полиномиальный
алгоритм может отличить ее от случайной последовательности
лишь с пренебрежимо малой вероятностью.
Понятие псевдослучайного генератора было введено в 1982 г. Блюмом и Микали [BM]. Мы приводим несколько
модифицированное определение из работы [Allen].
Определение 4.
Генератором называется полиномиальный
алгоритм (машина Тьюринга)  , который на входе , который на входе  длины длины
 выдает последовательность выдает последовательность 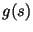 длины длины 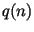 . Здесь . Здесь
 -- некоторый полином, -- некоторый полином,  и и 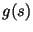 рассматриваются как
двоичные последовательности. Для произвольного
полиномиального алгоритма рассматриваются как
двоичные последовательности. Для произвольного
полиномиального алгоритма  , который на всех входах
выдает либо 0, либо 1 пусть , который на всех входах
выдает либо 0, либо 1 пусть
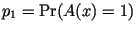 , ,
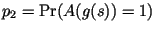 , где , где  -- строка, выбранная наудачу
из всех строк длины -- строка, выбранная наудачу
из всех строк длины 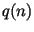 , а , а  -- строка, выбранная
наудачу из всех строк длины -- строка, выбранная
наудачу из всех строк длины  . Генератор . Генератор  называется
псевдослучайным, если
для любого полиномиального алгоритма называется
псевдослучайным, если
для любого полиномиального алгоритма  , для любого
полинома , для любого
полинома  и для всех достаточно больших и для всех достаточно больших 
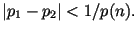
В определении 4 предполагается, что 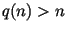 . На
практике интерес представляют генераторы, которые получают
на входе случайный источник . На
практике интерес представляют генераторы, которые получают
на входе случайный источник  длиной, скажем, в несколько
килобитов и "растягивают" его в псевдослучайную
последовательность, длина которой превосходит длину длиной, скажем, в несколько
килобитов и "растягивают" его в псевдослучайную
последовательность, длина которой превосходит длину  на
несколько порядков. на
несколько порядков.
Неформально определение псевдослучайного генератора можно
изложить так. Выбираем произвольный полиномиальный алгоритм
 с двоичным выходом. Затем выполняем два эксперимента. В
первом выбирается случайный источник с двоичным выходом. Затем выполняем два эксперимента. В
первом выбирается случайный источник  , дается генератору , дается генератору
 и полученная последовательность и полученная последовательность 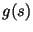 подается на вход
алгоритму подается на вход
алгоритму  . Во втором эксперименте выбирается случайная
последовательность такой же длины, как . Во втором эксперименте выбирается случайная
последовательность такой же длины, как 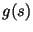 , и подается на
вход , и подается на
вход  . Результатами этих экспериментов являются
вероятности появления 1 на выходе . Результатами этих экспериментов являются
вероятности появления 1 на выходе  . Генератор называется
псевдослучайным, если разность этих вероятностей является
пренебрежимо малой величиной. . Генератор называется
псевдослучайным, если разность этих вероятностей является
пренебрежимо малой величиной.
Казалось бы, в приведенном выше определении 4
накладываются слишком сильные условия на те
последовательности, которые выдает псевдослучайный
генератор. В самом деле, возникает естественный вопрос,
нельзя ли требование неотличимости псевдослучайной
последовательности от случайной любым
полиномиальным алгоритмом ослабить и рассматривать только
алгоритмы из некоторого более узкого класса. Оказалось,
что ответ на этот вопрос отрицательный. Рассмотрим один из
тестов, называемый тестом следующего бита. Говорят, что
последовательность не проходит тест следующего
бита, если существует полиномиальный
алгоритм, который по начальному отрезку последовательности
предсказывает следующий бит с вероятностью по крайней мере
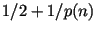 . Здесь . Здесь  -- некоторый полином, -- некоторый полином,  --
длина источника --
длина источника  . Тест следующего бита является
общепринятым критерием качества псевдослучайных
последовательностей в криптографии. Яо [Yao] доказал,
что генератор является псевдослучайным тогда и только
тогда, когда порождаемая им последовательность проходит
тест следующего бита. Иными словами, всякий эффективный
алгоритм, отличающий псевдослучайную последовательность от
случайной, может быть преобразован в эффективный алгоритм
предсказания следующего бита в этой псевдослучайной
последовательности. . Тест следующего бита является
общепринятым критерием качества псевдослучайных
последовательностей в криптографии. Яо [Yao] доказал,
что генератор является псевдослучайным тогда и только
тогда, когда порождаемая им последовательность проходит
тест следующего бита. Иными словами, всякий эффективный
алгоритм, отличающий псевдослучайную последовательность от
случайной, может быть преобразован в эффективный алгоритм
предсказания следующего бита в этой псевдослучайной
последовательности.
Из определения псевдослучайного генератора нетрудно
понять, что для его существования требуется существование
односторонней функции. Вопрос о достаточных условиях
оказался весьма нетривиальным. В результате интенсивных
исследований окончательное решение было получено в 1989 г. Импальяццо, Левиным и Луби (неоднородная модель вычислений)
и в 1990 г. Хостадом (однородная модель).
Теорема ([ILL], [H]).
Псевдослучайные генераторы существуют тогда и только тогда,
когда существуют односторонние функции.
Если в шифраторе гаммирования для выработки гаммы наложения
из секретного ключа использовать псевдослучайный генератор,
то будет получена криптосистема с секретным ключом, стойкая
против полиномиально ограниченного противника. Из данной
теоремы и из цитированных выше результатов Импальяццо и
Луби [IL] следует, что стойкие потоковые криптосистемы
с секретным ключом существуют тогда и только тогда, когда
существуют односторонние функции.
Помимо генераторов псевдослучайных последовательностей
существуют еще генераторы псевдослучайных функций и
генераторы псевдослучайных перестановок. Мы не приводим
определения ввиду их громоздкости и отсылаем читателя к
статьям Гольдрайха, Гольдвассер и Микали [GGM] и Луби
и Ракоффа [LR] соответственно. В работе [GGM]
доказано, что генераторы псевдослучайных функций существуют
тогда и только тогда, когда существуют генераторы
псевдослучайных последовательностей. В работе [LR]
аналогичный результат получен для генераторов
псевдослучайных перестановок. Из этого следует, что
предположение о существовании каждого из трех типов
псевдослучайных генераторов эквивалентно предположению о
существовании односторонних функций. Отметим также, что
Луби и Ракофф [LR] в качестве следствия установили,
что стойкие (против полиномиально ограниченного противника)
блоковые криптосистемы с секретным ключом существуют тогда
и только тогда, когда существуют односторонние функции.





Вперед: 15. Основные понятия теории доказательств с нулевым разглашением
Вверх: 14. Односторонние функции и псевдослучайные генераторы
Назад: 14.1.5 Функции с секретом
Содержание
Предметный указатель
|

