




Вперед: 6.3.2 Схема Диффи - Хеллмана по составному модулю
Вверх: 6.3 Теоретические результаты
Назад: 6.3 Теоретические результаты
Содержание
Предметный указатель
Протокол распределения ключей ((secret) key distribution
(agreement, sharing, exchange, generation) protocol) --
это протокол, который позволяет его участникам выработать
общую секретную информацию (общий секретный
ключ), обмениваясь сообщениями по
открытым для прослушивания каналам. Более подробно, пусть
перед началом протокола выбрано и сообщено участникам
некоторое большое натуральное число  , называемое
параметром безопасности.
Предположим также, что каждый из участников (которых можно
считать вероятностными полиномиальными от , называемое
параметром безопасности.
Предположим также, что каждый из участников (которых можно
считать вероятностными полиномиальными от  машинами
Тьюринга) имеет свой источник секретных случайных битов. В
протоколе может предполагаться наличие некоторого
дополнительного участника, пользующегося абсолютным
доверием всех остальных участников, которого мы будем
называть центром доверия.
Подчеркнем, что перед началом выполнения протокола не
предполагается наличие у участников какой-либо общей
секретной информации. В процессе выполнения протокола
участники обмениваются сообщениями по несекретным каналам
связи, после чего каждый участник вычисляет свой элемент
некоторого множества машинами
Тьюринга) имеет свой источник секретных случайных битов. В
протоколе может предполагаться наличие некоторого
дополнительного участника, пользующегося абсолютным
доверием всех остальных участников, которого мы будем
называть центром доверия.
Подчеркнем, что перед началом выполнения протокола не
предполагается наличие у участников какой-либо общей
секретной информации. В процессе выполнения протокола
участники обмениваются сообщениями по несекретным каналам
связи, после чего каждый участник вычисляет свой элемент
некоторого множества 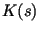 , называемого
пространством ключей. Если
все участники вычислили один и тот же элемент из , называемого
пространством ключей. Если
все участники вычислили один и тот же элемент из 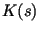 , то
этот элемент и является общим секретным ключом. Этот общий
секретный ключ не предполагается случайным элементом , то
этот элемент и является общим секретным ключом. Этот общий
секретный ключ не предполагается случайным элементом
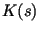 . Разумеется, необходимо, чтобы вероятность . Разумеется, необходимо, чтобы вероятность
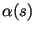 того, что все участники вычислили один и тот же
элемент, была достаточно большой или даже равнялась того, что все участники вычислили один и тот же
элемент, была достаточно большой или даже равнялась 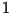 . .
Задача противника состоит в вычислении общего секретного
ключа. Для этого он может как просто подслушивать сообщения
участников друг другу (пассивный
противник (passive adversary,
eavesdropper)), так и вмешаться в выполнение протокола
путем замены сообщений участников своими сообщениями,
выдавая себя за одного из законных участников
(активный противник (active
adversary, impersonator)).
Определение.
Протокол распределения ключей называется
нестойким
(insecure), если существует полиномиальный от  вероятностный алгоритм (противник),
вычисляющий по данной открытой информации протокола (всегда
включающей параметр безопасности
вероятностный алгоритм (противник),
вычисляющий по данной открытой информации протокола (всегда
включающей параметр безопасности  ) и сообщениям,
передаваемым друг другу участниками протокола (множество
всех таких сообщений называется транскрипцией
диалога) общий секретный ключ с
вероятностью не менее ) и сообщениям,
передаваемым друг другу участниками протокола (множество
всех таких сообщений называется транскрипцией
диалога) общий секретный ключ с
вероятностью не менее
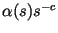 (где (где 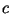 --
некоторая положительная константа) для бесконечного
множества параметров --
некоторая положительная константа) для бесконечного
множества параметров  . В противном случае протокол
распределения ключей называется стойким (secure). . В противном случае протокол
распределения ключей называется стойким (secure).
Отметим, что в случае активного противника ключи,
вырабатываемые законными участниками (вообще говоря,
различные для различных участников) зависят также и от
действий противника, поэтому здесь для стойкости нужно
потребовать, чтобы, каковы бы ни были эти действия
(ограниченные полиномиальными вычислительными ресурсами),
противник не мог вычислить с вышеуказанной вероятностью
ключ хотя бы одного законного участника. Конечно, если
противник может заставить участников вырабатывать различные
секретные ключи, то протокол непригоден для серьезного
применения.
Существуют теоретические результаты, которые показывают,
что задача обоснования стойкости протоколов распределения
ключей, по-видимому, сложнее других подобных задач,
возникающих в криптографии. Известно [IL], что
существование односторонних функций является необходимым
условием существования различных типов стойких криптосистем
и криптографических протоколов. Для некоторых
криптографических схем (например, для криптосистем с
секретным ключом и протоколов электронной подписи) это
условие одновременно является и достаточным. Предположение
о существовании односторонней перестановки представляется
более сильным, чем предположение о существовании
произвольной односторонней функции. Однако, как показали
Импальяццо и Рудих [IR], имеется оракул, относительно
которого существуют односторонние перестановки, но не
существует стойких протоколов распределения ключей. Здесь
уместно заметить, что отрицательные релятивизированные
(доказанные относительно некоторых оракулов) результаты
означают, что соответствующие нерелятивизированные
утверждения (например, что из существования односторонней
перестановки следует существование стойкого протокола
распределения ключей) не могут быть доказаны методами,
которые допускают релятивизацию. А таковыми являются почти
все (за редким исключением) известные на сегодняшний день в
математике методы. Таким образом, даже достаточно сильного
предположения о существовании односторонней перестановки
может оказаться недостаточно для доказательства
существования стойких протоколов распределения ключей.
Имеются и другие результаты (см. [Bra1], [Bra2],
[Rud], подтверждающие высказанный в начале абзаца
тезис.
Следует упомянуть, что в литературе встречаются утверждения
о том, что существование стойких криптосистем с открытым
ключом является достаточным условием для существования
стойких протоколов распределения ключей (см. [DH],
[IR], [Rud]), из чего делается вывод о том, что
для существования последних достаточно существования
функций с секретом. При этом сам тезис либо вообще никак не
обосновывается, либо указывается, что один из участников
протокола, используя криптосистему, посылает секретный ключ
другому, выбрав его случайным образом из пространства
ключей. Мы считаем, что протокол распределения ключей
должен обеспечивать равноправие участников в выборе ключа,
а также решение указанной проблемы аутентификации
участников. Поэтому к заявлениям о достаточности
существования стойких криптосистем с открытым ключом для
существования стойких протоколов распределения ключей, при
отсутствии формальных определений и доказательств, мы
относимся скептически.





Вперед: 6.3.2 Схема Диффи - Хеллмана по составному модулю
Вверх: 6.3 Теоретические результаты
Назад: 6.3 Теоретические результаты
Содержание
Предметный указатель
|

