




Вперед: 4.6 Теоретические результаты
Вверх: 4. Протоколы электронной подписи
Назад: 4.4 Реализация схем подписи на интеллектуальных карточках
Содержание
Предметный указатель
4.5 Проблемы арбитража
При описании схем электронной подписи авторы обычно
приводят два алгоритма: алгоритм генерации подписи и
алгоритм ее верификации. Однако для практического
применения таких схем необходимо еще описание действий в
случае возникновения споров о корректности данной
конкретной подписи. Для этого в схеме должен быть
предусмотрен арбитраж. Вопросам арбитража в литературе
уделяется незначительное внимание. По-видимому, это связано
с тем, что разработка арбитражных процедур является
прерогативой каждого конкретного пользователя, вводящего в
эксплуатацию схему электронной подписи. По крайней мере,
нам не удалось обнаружить ни одной работы, в которой
достаточно подробно рассматривались бы математические
аспекты арбитража. В результате данный подраздел не носит
обзорного характера, а содержит результаты анализа
проблемы.
В дальнейшем изложении для определенности используется
отечественный стандарт на схему электронной цифровой
подписи (см. подраздел 4.2.5). Для
других схем подписи проблемы арбитража аналогичны, за
исключением схем с интерактивной процедурой верификации
(см. подраздел 4.3.2).
Арбитраж необходим для разрешения споров, т. е. ситуаций,
когда один из пользователей (B) предъявляет сообщение  и
подпись и
подпись 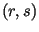 , утверждая, что она была сгенерирована
пользователем A, а A отказывается признать эту подпись
своей. Здесь возникает третья сторона -- арбитр, который
должен дать заключение об авторстве подписи. Роль арбитра в
этом плане аналогична роли графолога, дающего заключение о
подлинности обычной подписи. С юридической точки зрения,
по-видимому, единственным основанием для разбора подобных
споров в суде может быть подписание каждым пользователем при
подключении к системе специального документа, в котором этот
пользователь принимает все "правила игры", вплоть до
судебной ответственности. При разборе дела в суде арбитр
выступает как эксперт, дающий заключение о подлинности
электронной подписи. , утверждая, что она была сгенерирована
пользователем A, а A отказывается признать эту подпись
своей. Здесь возникает третья сторона -- арбитр, который
должен дать заключение об авторстве подписи. Роль арбитра в
этом плане аналогична роли графолога, дающего заключение о
подлинности обычной подписи. С юридической точки зрения,
по-видимому, единственным основанием для разбора подобных
споров в суде может быть подписание каждым пользователем при
подключении к системе специального документа, в котором этот
пользователь принимает все "правила игры", вплоть до
судебной ответственности. При разборе дела в суде арбитр
выступает как эксперт, дающий заключение о подлинности
электронной подписи.
Процедура арбитража
1.
B предъявляет арбитру сообщение  и подпись и подпись
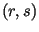 . .
2.
Арбитр вызывает A и требует предъявить секретный
ключ  . Если A отказывается, арбитр дает заключение, что
подпись подлинная. . Если A отказывается, арбитр дает заключение, что
подпись подлинная.
3.
Арбитр выбирает из сертифицированного справочника
открытый ключ пользователя A и проверяет его соответствие
секретному ключу. Если ключи соответствуют друг другу,
переходит на п. 4. При обнаружении несоответствия обращается
в центр доверия, который ведет сертифицированный справочник,
и требует подписанный A (обычной подписью или печатью)
документ, подтверждающий подлинность открытого
ключа. Несоответствие значения ключа в справочнике значению
в документе -- ситуация неординарная и маловероятная, но, в
принципе, возможная (например, ошибка персонала). В таком
случае необходимо серьезное расследование. Арбитр признает
подпись, предъявленную B, подлинной. Все издержки -- за
счет центра доверия. Если ключи в документе и в справочнике
совпадают, то это означает, что A предъявил некорректный
секретный ключ. Арбитр признает подпись, предъявленную B
подлинной.
4.
Арбитр вычисляет 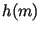 и и
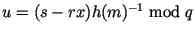 . Проверяет, что . Проверяет, что
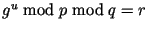 . Если да, то
подпись признается подлинной.
Разумеется, эта процедура выполняется только в том случае,
когда подстановка значений . Если да, то
подпись признается подлинной.
Разумеется, эта процедура выполняется только в том случае,
когда подстановка значений 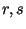 и и  в проверочное
соотношение дает положительный результат, а A отказывается
признавать подпись. В принципе, арбитру следует начинать
разбор спора именно с этого, хотя маловероятно, чтобы на
этом разбор закончился, ведь пользователь A может
самостоятельно выполнить алгоритм верификации. Существует,
пожалуй, единственный сценарий, когда положительный
результат верификации, выполненной арбитром, может убедить
A: пользователь A "запамятовал", действительно ли он
подписывал сообщение в проверочное
соотношение дает положительный результат, а A отказывается
признавать подпись. В принципе, арбитру следует начинать
разбор спора именно с этого, хотя маловероятно, чтобы на
этом разбор закончился, ведь пользователь A может
самостоятельно выполнить алгоритм верификации. Существует,
пожалуй, единственный сценарий, когда положительный
результат верификации, выполненной арбитром, может убедить
A: пользователь A "запамятовал", действительно ли он
подписывал сообщение  , и к тому же он не доверяет тем
аппаратным и программным средствам, которые предоставлены
ему для верификации. Такая возможность лишний раз
подчеркивает, что арбитр в своей работе должен пользоваться
независимыми аппаратными и программными средствами. , и к тому же он не доверяет тем
аппаратным и программным средствам, которые предоставлены
ему для верификации. Такая возможность лишний раз
подчеркивает, что арбитр в своей работе должен пользоваться
независимыми аппаратными и программными средствами.
Никакая процедура арбитража не может, конечно, быть полной,
т. е. описывать все возможные ситуации и соответствующие
действия арбитра. Более того, в некоторых ситуациях не
очевидно, какое решение ему следует принять. Например, B
предъявляет 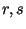 и утверждает, что это -- подпись под
сообщением и утверждает, что это -- подпись под
сообщением  . A признает, что эта подпись была
сгенерирована им, но под сообщением . A признает, что эта подпись была
сгенерирована им, но под сообщением 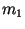 , причем , причем
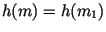 . Ясно, что кто-то из двоих нашел коллизию для
хэш-функции. Быть может, это говорит о слабости хэш-функции
и ее следует заменить. Но что делать арбитру с данным
конкретным спором? Бросить жребий или оставить эту
головоломку суду? Пользователям, однако, уже при
подключении к системе необходимо знать, какое решение будет
принято в такой ситуации. . Ясно, что кто-то из двоих нашел коллизию для
хэш-функции. Быть может, это говорит о слабости хэш-функции
и ее следует заменить. Но что делать арбитру с данным
конкретным спором? Бросить жребий или оставить эту
головоломку суду? Пользователям, однако, уже при
подключении к системе необходимо знать, какое решение будет
принято в такой ситуации.
Одна из проблем, связанных с приведенной выше процедурой
арбитража, состоит в том, что арбитр получает секретный
ключ  . Справедливости ради, следует отметить, что если
арбитр нечестный, то никаких способов защиты пользователей
от него не может быть в принципе. . Справедливости ради, следует отметить, что если
арбитр нечестный, то никаких способов защиты пользователей
от него не может быть в принципе.
В заключение сформулируем основные принципы, на которых
основываются процедуры арбитража.
1.
Каждый пользователь должен самостоятельно
генерировать свой секретный ключ. Создание специального
центра, генерирующего ключи, может обезопасить
пользователей от слабых ключей, но полностью исключает
возможность арбитража и решения споров в суде.
2.
Арбитраж возможен только для "настоящих" схем
подписи. Схемы, основанные на криптографии с секретным
ключом (аутентификаторы или имитовставки) могут
использоваться только для передачи сообщений между
полностью доверяющими друг другу партнерами, у которых не
может возникнуть никаких споров.
3.
Арбитраж невозможен, если аппаратура, на которой
выполняется алгоритм генерации и (или) верификации подписи,
содержит какие-либо элементы, не контролируемые
пользователем полностью ("черные ящики" или защищенные
участки памяти). Поэтому, ценность для банковского дела
технологий, подобных предлагаемой фирмой IBM,
представляется сомнительной.





Вперед: 4.6 Теоретические результаты
Вверх: 4. Протоколы электронной подписи
Назад: 4.4 Реализация схем подписи на интеллектуальных карточках
Содержание
Предметный указатель
|

