1. Прямая задача. Пусть вертикальный
уступ (сброс) простирается бесконечно вдоль оси y (рис. 1.5).
Наблюдения производятся вдоль оси ( x), ( y=z=0), расположенной вкрест простирания сброса. Если глубина до кровли z1 и z2 , а амплитуда
уступа 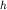 , то, согласно (1.10), , то, согласно (1.10),
![$\Delta g=G(\sigma-\sigma_0) \int\limits_0^{+\infty}dx\int\limits_{-\infty}^{\infty}dy \int\limits_{z_1}^{z^2}\frac{dz}{\left[ (\bar x -x)^2+\bar y^2+\bar z^2\right]^{3/2}}.$](http://images.geo.web.ru/pubd/2001/11/05/0001161636/tex/formula1065.gif) | (1.13) |
В общем случае выражение интеграла
имеет громоздкий вид. В частности, полная максимальная аномалия над
уступом (разность силы тяжести между поднятым и опущенным крылом)
определится следующей формулой:
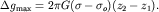 | (1.14) |
Над уступом (x=0) аномалия равна половине максимальной.
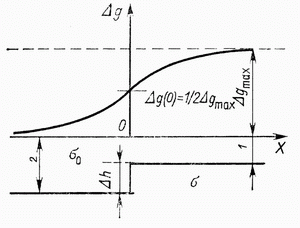 | | Рис.1.5 Гравитационное поле над уступом (сбросом) |
2. Обратная задача. Из (1.14) можно определить
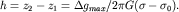
В теории гравиразведки доказано, что примерная
глубина расположения середины высоты уступа 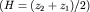 равна равна 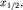 т.е. абсциссе точки, в которой т.е. абсциссе точки, в которой 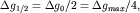 где где 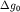 - аномалия над уступом,
а - аномалия над уступом,
а 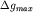 - полная аномалия. Практически
для определения - полная аномалия. Практически
для определения 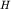 на кривой на кривой 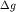 находится местоположение
сброса находится местоположение
сброса 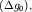 и в масштабе профиля рассчитывается и в масштабе профиля рассчитывается
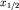 - расстояние от сброса до точки, в которой - расстояние от сброса до точки, в которой
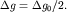 Зная Зная 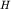 и и 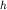 , легко определить глубины до приподнятого , легко определить глубины до приподнятого 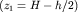 и опущенного и опущенного 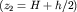 крыла. крыла.
1. Прямая задача. Для тел более сложной формы расчет 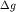 представляет
большие трудности и выполняется либо на вычислительных машинах, либо
графическим путем с помощью различных палеток. Для вычислений аномалий
над телами с сечением любой произвольной формы и вытянутыми вдоль
оси (двухмерные тела) применяется палетка Гамбурцева. Палетка имеет
вид, показанный на рис. 1.6. представляет
большие трудности и выполняется либо на вычислительных машинах, либо
графическим путем с помощью различных палеток. Для вычислений аномалий
над телами с сечением любой произвольной формы и вытянутыми вдоль
оси (двухмерные тела) применяется палетка Гамбурцева. Палетка имеет
вид, показанный на рис. 1.6.
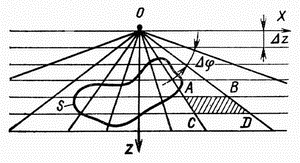 | | Рис.1.6 Палетка Гамбурцева для вычисления притяжения двухмерных тел |
Здесь из точки О через один и тот же угол 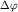 проведены радиусы, а через равные расстояния проведены радиусы, а через равные расстояния 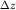 - параллельные линии. - параллельные линии.
Сила тяжести 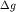 в точке О
за счет притяжения бесконечной горизонтальной призмой сечением в
виде трапеции ABCD одинакова для любой из таких призм и равна в точке О
за счет притяжения бесконечной горизонтальной призмой сечением в
виде трапеции ABCD одинакова для любой из таких призм и равна
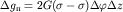 | (1.15) |
В самом деле, воспользуемся формулой притяжения
бесконечно длинным цилиндром (1.12), в которую вместо \lambda
подставим массу элементарной призмы сечением dxdz:
Притяжение бесконечно длинной
призмой любого сечения может быть рассчитано по формуле:
Заменив 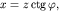 получим получим
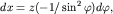 но
но 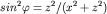 , поэтому , поэтому
где 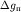 - цена одной трапеции (цена
палетки), равная - цена одной трапеции (цена
палетки), равная 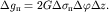
Подобрав 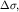 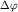 и и 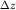 такими, чтобы такими, чтобы 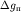 равнялось какому-нибудь постоянному значению (например, 0,1 мГал), легко рассчитать в точке О аномалию от призмы любого
сечения, для чего надо подсчитать число трапеций, покрывающих сечение
исследуемого тела (n). Аномалия равнялось какому-нибудь постоянному значению (например, 0,1 мГал), легко рассчитать в точке О аномалию от призмы любого
сечения, для чего надо подсчитать число трапеций, покрывающих сечение
исследуемого тела (n). Аномалия 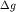 равна
n, умноженному на цену палетки и масштабный коэффициент равна
n, умноженному на цену палетки и масштабный коэффициент
где 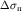 и и 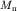 - избыточная плотность и масштаб палетки, а
- избыточная плотность и масштаб палетки, а  и и 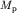 - избыточная плотность и масштаб разреза. - избыточная плотность и масштаб разреза.
Таким образом, аномалия над
двухмерным телом любого сечения с помощью палетки Гамбурцева рассчитывается
по формуле:
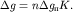 | (1.16) |
2. Обратная задача. Используя (1.16) с
помощью палетки Гамбурцева, можно выяснить форму и положение сечения
возмущающего двухмерного аномалосоздающего объекта. Для этого надо
знать избыточную плотность  , оценить аналитическим способом положение ее центра и для нескольких
точек графика , оценить аналитическим способом положение ее центра и для нескольких
точек графика 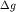 построить возможные сечения возмущающего
тела. Среднее из них характеризует примерное сечение тела. построить возможные сечения возмущающего
тела. Среднее из них характеризует примерное сечение тела.
Для более сложных форм аномалосоздающих объектов прямые задачи гравиразведки решаются
численными методами с помощью ЭВМ. За основу берется формула для
гравитационной аномалии, созданной любым телом с постоянной или переменной
избыточной плотностью (1.10). Практически численный метод сводится
к разбиению объекта на элементарные массы, ячейки - например,
шаровой или кубической формы. Гравитационный эффект таких масс рассчитывается
по формуле (1.9), а затем ведется их суммирование по всему объему
объекта. Счет можно реализовать с помощью ЭВМ.
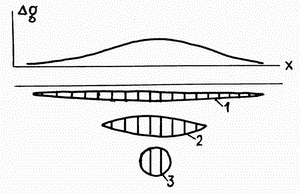 | | Рис.1.7 К неоднозначности решения обратной задачи гравиразведки |
Обратные задачи решаются методом сравнения полевой
аномалии с теоретически рассчитанными, у которых геометрические параметры
и избыточные плотности постепенно изменяются до получения наименьших
расхождений между кривыми. Если прямые задачи, как и всякие прямые
задачи математической физики, однозначны, то обратные задачи неоднозначны
(см. 3). На рис. 1.7 приведен схематический пример того, как тела
разного сечения и глубины залегания даже при постоянной избыточной
плотности могут создать одинаковую аномалию силы тяжести.
Основным измеряемым параметром в гравиразведке является ускорение
силы тяжести  , которое определяется либо абсолютно, либо
относительно. При абсолютных измерениях получают полное (наблюденное)
значение ускорения , которое определяется либо абсолютно, либо
относительно. При абсолютных измерениях получают полное (наблюденное)
значение ускорения 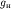 , при относительных -
его приращение относительно некоторой исходной точки , при относительных -
его приращение относительно некоторой исходной точки 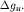
Методы измерения ускорения силы тяжести и его приращения
делятся на динамические и статические. Под динамическими понимаются
такие методы, в которых наблюдается движение тела под действием силы
тяжести (качание маятника, свободное падение тел и др.) В этом случае
g определяется через параметры движения тела и параметры
установки. В статических методах действие силы тяжести компенси\-руется
(например, силой упругости пружины), а g определяется по
изменению статического положения равновесия тела.
Реже в гравиразведке измеряются вторые производные
гравитаци\-онного потенциала 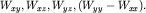
а). Наиболее используемый динамический метод - маятниковый. Для
абстрактного объекта - математического маятника - период
колебаний
где  - длина маятника, - длина маятника,  - ускорение
силы тяжести, - ускорение
силы тяжести,  - максимальное значение угла
отклонения маятника от вертикали. Эта формула остается справедливой
и для реального объекта - физического маятника, если в качестве - максимальное значение угла
отклонения маятника от вертикали. Эта формула остается справедливой
и для реального объекта - физического маятника, если в качестве
 взять так называемую приведенную длину взять так называемую приведенную длину 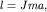 где где 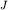 - момент инерции маятника, - момент инерции маятника, 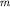 - масса, - масса,  - расстояние от центра тяжести до оси вращения. При малых - расстояние от центра тяжести до оси вращения. При малых  формула для периода принимает
вид формула для периода принимает
вид 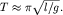 Точность определения периода возрастает
при увеличении времени наблюдения за колебаниями маятника. Для абсолютных
измерений ускорения силы тяжести необходимо измерять длину маятника.
Зная Точность определения периода возрастает
при увеличении времени наблюдения за колебаниями маятника. Для абсолютных
измерений ускорения силы тяжести необходимо измерять длину маятника.
Зная 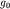 и и 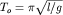 на исходной
точке, а также на исходной
точке, а также 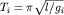 на i-той
точке, можно выполнить относительные измерения в двух точках:
по формуле на i-той
точке, можно выполнить относительные измерения в двух точках:
по формуле 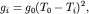 т.е. в относительных измерениях длину определять не надо. т.е. в относительных измерениях длину определять не надо.
Хотя маятниковые приборы и подвержены воздействию
температуры, влажности и других факторов, они характеризуются очень
медленным и плавным сползанием нуль-пункта (изменением зависимости
показаний в одной и той же точке от времени, вызванным старением
системы).
При измерениях маятниковыми приборами в движении,
например, при морских съемках, влияние качки можно существенно снизить,
если применять несколько маятников, закрепленных на одном основании.
В этом случае их колебания обычно сводят к колебаниям одного эмпирического
маятника, используя сложный математический аппарат.
Погрешность абсолютных измерений ускорения силы
тяжести маятниковыми приборами можно довести до 1 - 3 мГал, а относительных
- при наземных исследованиях - до 0.1 мГал, при морских съемках
- до 5 - 10 мГал.
б). Определение абсолютного значения ускорения
силы тяжести можно проводить методом свободного падения, когда измеряется
время свободного падения тела и расстояние, пройденное телом. Измерения
отличаются большой трудоемкостью и выполняются на обсерваториях,
где точность в определении  можно довести до 0,01 мГал. можно довести до 0,01 мГал.
в). В настоящее время известны методы абсолютных
и относительных измерений силы тяжести, основанные на изучении колебаний
струн. В них измеряется частота колебаний струны, ее длина и масса.
В результате можно рассчитать  или или 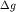 . .
Назад| Вперед
| 
