| Публикации на сервере (6) |
 17.09.2004 |
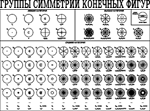
Таблица групп симметрии конечных фигур
17.09.2004 |
Таблица групп симметрии конечных фигур
Плакаты А0, и А3.
На плакате показаны стереографические проекции элементов симметрии,
символы Шёнфлиса и символы Браве в их учебном варианте, максимально отражающем строение групп.
Таблица разделена на три ячейки по категориям: низшую (8 групп), высшую (7 групп) и среднюю
(13 счётных серий групп симметрии).
Таблица содержит как группы, описывающие симметрию кристаллов (их всего 32), так и группы,
не допускающие решёточное строение описываемого объекта, содержащие оси . . .
|
 |
 20.03.2007 |
Делоне Б.Н., Сандакова Н.Н. Теория стереоэдров. Тр. МИАН, 1961, 64, 28-51
20.03.2007 |
Делоне Б.Н., Сандакова Н.Н. Теория стереоэдров. Тр. МИАН, 1961, 64, 28-51
Делоне Б.Н., Сандакова Н.Н. Теория стереоэдров. Тр. МИАН, 1961, 64, 28-51
Работа Б.Н. Делоне и Н.Н. Сандаковой является продолжением трудов Е.С. Фёдорова о паралеллоэдрах и стереоэдрах. Именно в этой работе впервые показана конечность числа граней
стереоэдров в трёхмерном евклидовом пространстве (n<390).
Численное значение этой оценки явно завышено, поэтому продолжаются работы по её улучшению как математиками, так и кристаллографами - А.С. Тарасовым ( О сложности выпуклых
стереоэдров . . .
|
|
 20.03.2007 |
А.К. Болдырев. Комментарий к работе Е.С. Фёдорова: DAS KRYSTALLREICH (Царство кристаллов)., Л., 1926.
20.03.2007 |
А.К. Болдырев. Комментарий к работе Е.С. Фёдорова: DAS KRYSTALLREICH (Царство кристаллов)., Л., 1926.
А.К. Болдырев. Комментарий к работе Е.С. Фёдорова: DAS KRYSTALLREICH., Л., Изд-во АН СССР, 1926, 72С.
Книга полезна для понимания трудов Е.С. Фёдорова. Рекомендуется специалистам и студентам старших курсов для углублённого изучения кристаллографии, а также всем интересующимся
историей кристаллографической науки.
Сканировали Я.В. Кучериненко и Д.Г. Степенщиков
Благодарность А.К. Шпаченко, Кольскому Научному Центру РАН и Ю.Л. Войтеховскому . . .
|
 |
 19.03.2007 |
Н.К. Разумовский Стереографические проекции., Л.: КУБУЧ, 1927, 94С. (PDF, 5.31Mb)
19.03.2007 |
Н.К. Разумовский Стереографические проекции., Л.: КУБУЧ, 1927, 94С. (PDF, 5.31Mb)
Н.К. Разумовский Стереографические проекции., Л.: КУБУЧ, 1927, 94С.
Книга рекомендована известным кристаллографом, профессором Анатолием Капитоновичем Болдыревым (1883-1946) для подробного изучения стереографических проекций и работы с сетками
Вульфа .
(А.К. Болдырев. Кристаллография. Л., КУБУЧ, 1931)
Ориентирована на кристаллографические задачи, но может быть полезна в петрологии, структурной геологии, а также студентам и специалистам других геологических специальностей.
Книгу отскани . . .
|
 |
 17.09.2004 |
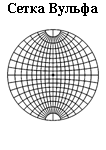
Сетки Вульфа, сетки Федорова и сетки Болдырева
17.09.2004 |
Сетки Вульфа, сетки Федорова и сетки Болдырева
Представленные сетки применяются для работы со стереографическими проекциями, а именно,
для нанесения проекций направлений исходя из их сферических координат, измерения углов между
направлениями, плоскостями и ряда других задач. Наиболее известны сетки Вульфа.
Сетки Болдырева и сетки Фёдорова представляют скорее исторический, чем практический интерес,
однако все представленные сетки выполнены с высоким качеством и в разных вариантах,
так, что при желании их практического использовани . . .
|
 |
 17.09.2004 |
32 класса симметрии кристаллов
17.09.2004 |
32 класса симметрии кристаллов
Плакаты А0, А3, А4 .
На плакате показаны стереографические проекции элементов симметрии; даны обозначения Шёнфлиса;
международные обозначения (символы Германа-Могена), как сокращённые, так и полные; символы Браве,
в том числе учебные. Все 32 группы симметрии разделены на
категории по соотношениям между
a, b, c (отрезки координатной системы) и, более детально, на сингонии по соотношениям между
. . .
|
 |
 17.09.2004 |
Таблица наиболее типичных координационных полиэдров
17.09.2004 |
Таблица наиболее типичных координационных полиэдров
Рисунок формата А4 при 150 dpi.
При составлении таблицы использовалась книга А.Уэллса "Структурная неорганическая химия" Т.1-3, 1987,
а также программа Balls&Sticks v.1.47. Автор заинтересован в вашей информации, какие на ваш взгляд
полиэдры можно было бы добавить к таблице. Обязательное условие: этот полиэдр должен присутствовать
хотя бы в одной реально существующей структуре кристалла. . . .
|
 |
|
|
|
|

