



Next: 3 изоморфизм евклидовых пространств
Up: 1 n-мерное пространство. Линейные
Previous: 1 Линейное (аффинное) -мерное
Subsections
В предыдущем параграфе линейное (аффинное) пространство было
определено как множество элементов (векторов) с заданными в нем
операциями умножения на числа и сложения.
С помощью этих операций можно сформулировать, что такое прямая,
плоскость, число измерений пространства, что такое параллельные
прямые и т.д.
Однако этих понятий недостаточно, чтобы охватить все многообразие
фактов, составляющих содержание так называемой евклидовой
геометрии. Например, в одних терминах сложения и умножения на число мы
не сможем дать определение длины вектора, угла между векторами,
скалярного произведения векторов и т.д. Ввести эти понятия проще
всего следующим образом.
Выберем в качестве основного понятие скалярного произведения,
которое определим аксиоматически.
В терминах сложения векторов, умножения их на числа и скалярного
произведения векторов мы сможем развить всю евклидову геометрию.
Определение 2.1
Будем говорить, что в вещественном пространстве 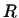 определено
скалярное произведение,
если каждой паре векторов определено
скалярное произведение,
если каждой паре векторов 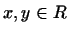 поставлено в соответствие действительное число, которое обозначим
через
поставлено в соответствие действительное число, которое обозначим
через  причем это соответствие обладает следующими свойствами
(удовлетворяет следующим аксиомам):
1 причем это соответствие обладает следующими свойствами
(удовлетворяет следующим аксиомам):
1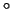
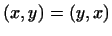 , т.е. скалярное произведение
симметрично. , т.е. скалярное произведение
симметрично.
2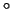
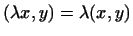 , где , где
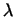 -- действительное число. -- действительное число.
3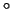
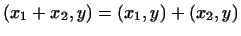 (дистрибутивность
скалярного произведения). (дистрибутивность
скалярного произведения).
4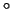 Скалярное произведение вектора с самим собой
неотрицательно:
Скалярное произведение вектора с самим собой
неотрицательно:
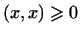 , и обращается в нуль, лишь
если , и обращается в нуль, лишь
если 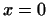 . .
Аффинное пространство, в котором определено скалярное произведение,
удовлетворяющее условиям 1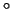 -4 -4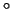 , мы называем
евклидовым. , мы называем
евклидовым.
Примеры
1. Под векторами пространства 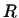 мы будем понимать
векторы изучаемого в элементарной геометрии трехмерного пространства
(пример 1 1). Скалярное произведение векторов определим
как произведение их длин на косинус угла между ними. Можно проверить,
что аксиомы 1 мы будем понимать
векторы изучаемого в элементарной геометрии трехмерного пространства
(пример 1 1). Скалярное произведение векторов определим
как произведение их длин на косинус угла между ними. Можно проверить,
что аксиомы 1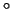 -4 -4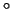 действительно выполнены. Мы
предоставляем эту проверку читателю. действительно выполнены. Мы
предоставляем эту проверку читателю.
2. Векторами пространства 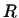 мы назовем всякую систему мы назовем всякую систему
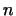 действительных чисел действительных чисел
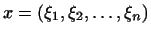 . Сложение
векторов и умножение их на число определим так
(пример 2 1): . Сложение
векторов и умножение их на число определим так
(пример 2 1):
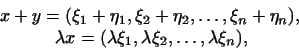 где
где
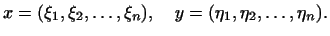 Скалярное произведение векторов
Скалярное произведение векторов 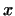 и и 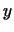 определим формулой определим формулой
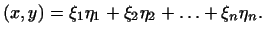
Легко проверить, что аксиомы 1 -3 -3 действительно
выполнены. Аксиома 4 действительно
выполнены. Аксиома 4 также справедлива, так как также справедлива, так как
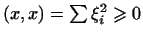 и и
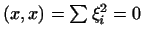 только при только при
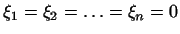 . .
3. Рассмотрим пример более общий, чем пример 2.
Вектор по-прежнему определим как совокупность 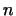 действительных
чисел. Сложение векторов и умножение их на числа определим так же, как
в примере 2. действительных
чисел. Сложение векторов и умножение их на числа определим так же, как
в примере 2.
Зададимся некоторой матрицей
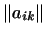 . Скалярное произведение
векторов . Скалярное произведение
векторов 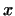 и и 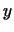 определим формулой определим формулой
Посмотрим, какие условия нужно наложить на матрицу
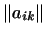 , чтобы
выражение, определяемое формулой (1), действительно удовлетворяло всем
аксиомам скалярного произведения. , чтобы
выражение, определяемое формулой (1), действительно удовлетворяло всем
аксиомам скалярного произведения.
Непосредственной проверкой убеждаемся в том, что аксиомы 2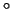 и
3 и
3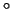 выполнены для всякой матрицы выполнены для всякой матрицы
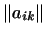 . Для того чтобы
была выполнена аксиома 1 . Для того чтобы
была выполнена аксиома 1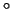 , т.е. чтобы выражение , т.е. чтобы выражение  было
симметричным относительно было
симметричным относительно 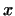 и и 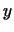 , необходимо и достаточно, чтобы , необходимо и достаточно, чтобы
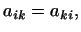 |
(2) |
т.е. чтобы матрица
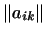 была симметричной. была симметричной.
Аксиома 4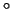 требует, чтобы выражение требует, чтобы выражение
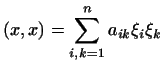 |
(3) |
было неотрицательно для любых
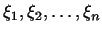 и обращалось в
нуль, лишь если и обращалось в
нуль, лишь если
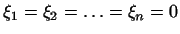 . .
Однородный многочлен (``квадратичная форма''), определяемый формулой
(3), называется
положительно определенным,
если он принимает лишь неотрицательные значения и обращается в нуль,
лишь когда все 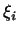 равны нулю. Аксиома 4 равны нулю. Аксиома 4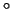 требует,
следовательно, чтобы квадратичная форма (3) была положительно
определенной. требует,
следовательно, чтобы квадратичная форма (3) была положительно
определенной.
Итак, всякая матрица
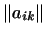 задает скалярное произведение,
определяемое формулой (1), если только эта матрица симметрична
[условие (2)] и соответствующая ей квадратичная форма -- положительно
определенная. задает скалярное произведение,
определяемое формулой (1), если только эта матрица симметрична
[условие (2)] и соответствующая ей квадратичная форма -- положительно
определенная.
Если в качестве матрицы
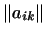 взять единичную матрицу,
т.е. положить взять единичную матрицу,
т.е. положить 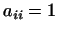 и и
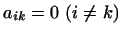 , то скалярное
произведение , то скалярное
произведение  примет вид примет вид
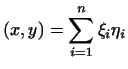 и мы получим евклидово пространство, определенное в примере 2.
и мы получим евклидово пространство, определенное в примере 2.
Упражнение
Показать, что матрица
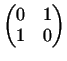 непригодна для построения скалярного произведения (соответствующая ей
квадратичная форма не является положительно определенной), а матрица
непригодна для построения скалярного произведения (соответствующая ей
квадратичная форма не является положительно определенной), а матрица
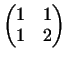 определяет скалярное
произведение, удовлетворяющее аксиомам 1 определяет скалярное
произведение, удовлетворяющее аксиомам 1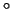 -4 -4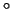 . .
В дальнейшем ( 6) будут указаны простые условия,
дающие возможность проверить, будет ли данная квадратичная форма
положительно определенной.
4. Векторами пространства 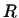 мы будем называть непрерывные функции,
заданные на интервале мы будем называть непрерывные функции,
заданные на интервале 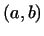 ; скалярное произведение таких функций
определим как
интеграл
их произведения ; скалярное произведение таких функций
определим как
интеграл
их произведения
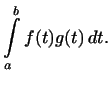 Можно проверить, что при таком определении скалярного
произведения аксиомы 1
Можно проверить, что при таком определении скалярного
произведения аксиомы 1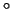 -4 -4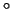 выполнены. выполнены.
5. Будем считать векторами многочлены от 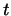 степени не выше степени не выше
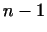 . Скалярное произведение двух многочленов определим как и в
предыдущем примере: . Скалярное произведение двух многочленов определим как и в
предыдущем примере:
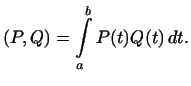 Аксиомы 1
Аксиомы 1 -4 -4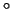 проверяются как и в примере 4. проверяются как и в примере 4.
Определим с помощью введенного понятия скалярного произведения длину
вектора и угол между векторами.
Определение 2.2
Длиной вектора
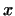 в евклидовом пространстве называется число в евклидовом пространстве называется число
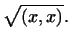 |
(4) |
Длину вектора 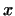 будем обозначать через будем обозначать через 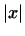 . .
Естественно пожелать, чтобы угол между векторами, длина вектора и
скалярное произведение были связаны обычным соотношением: скалярное
произведение векторов равно произведению их длин на косинус угла между
ними. Так как в этой фразе смысл всех слов, кроме слов ``угол между
векторами'', нам уже известен, то этим предписывается следующее
Определение 2.3
Углом между векторами
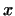 и и 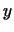 мы назовем число мы назовем число
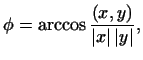 т.е. положим
т.е. положим
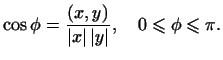 |
(5) |
Векторы 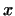 и и 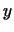 называются
ортогональными,
если угол между
ними равен называются
ортогональными,
если угол между
ними равен
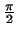 , т.е. если , т.е. если
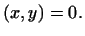
С помощью введенных понятий можно перенести на евклидовы пространства
ряд теорем элементарной геометрии 2.4.
Рассмотрим один пример. Если 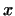 и и 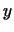 -- ортогональные векторы, то -- ортогональные векторы, то
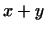 естественно считать диагональю прямоугольника со сторонами естественно считать диагональю прямоугольника со сторонами 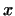 и
и 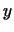 . Докажем, что . Докажем, что
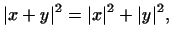 т.е. квадрат длины диагонали прямоугольника равен сумме
квадратов длин двух его непараллельных сторон (теорема Пифагора).
т.е. квадрат длины диагонали прямоугольника равен сумме
квадратов длин двух его непараллельных сторон (теорема Пифагора).
Доказательство. По определению квадрата длины вектора
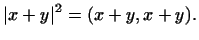 В силу дистрибутивности скалярного произведения
(аксиома 3
В силу дистрибутивности скалярного произведения
(аксиома 3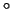 ) )
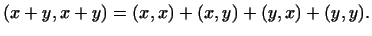 В силу ортогональности векторов
В силу ортогональности векторов 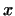 и и 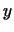
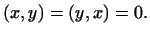 Следовательно,
Следовательно,
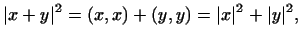 что и требовалось доказать.
что и требовалось доказать.
Эту теорему можно обобщить: если векторы
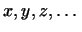 попарно ортогональны, то
попарно ортогональны, то
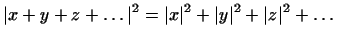
В предыдущем пункте у нас остался пробел. Мы определили угол 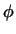 между векторами
между векторами 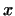 и и 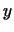 формулой формулой
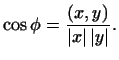
Для того чтобы можно было определить 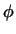 из этого равенства, нужно
доказать, что из этого равенства, нужно
доказать, что
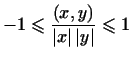 или, что то же самое, что
или, что то же самое, что
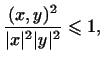 т.е.
т.е.
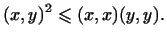 |
(6) |
Это неравенство называется
неравенством Коши--Буняковского.
Итак, для того чтобы иметь право определить угол между двумя
векторами формулой (5), мы должны доказать неравенство
Коши-Буняковского 2.5.
Чтобы доказать его, рассмотрим вектор 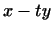 , где , где 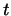 -- произвольное
действительное число. Согласно аксиоме 4 -- произвольное
действительное число. Согласно аксиоме 4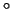 скалярного
произведения скалярного
произведения
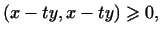 т.е. для любого
т.е. для любого 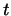
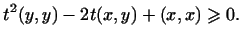
Мы видим, что стоящий слева квадратный относительно 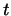 трехчлен
принимает лишь неотрицательные значения. Следовательно, дискриминант
уравнения трехчлен
принимает лишь неотрицательные значения. Следовательно, дискриминант
уравнения
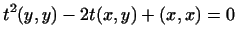 не может быть положительным, т.е.
не может быть положительным, т.е.
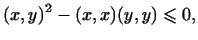 что и требовалось доказать.
что и требовалось доказать.
Упражнение
Доказать, что знак равенства в (6) имеет место тогда и только тогда,
когда векторы 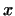 и и 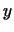 линейно зависимы. линейно зависимы.
Примеры
Мы доказали неравенство (6) для аксиоматически заданного евклидова
пространства. Разберем, как выглядит это неравенство в приведенных
выше (п.1) примерах евклидовых пространств.
1. В примере 1 неравенство (6) не означает
ничего нового (см. сноску).
2. Так как в примере 2 скалярное произведение
задается формулой
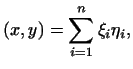 то
то
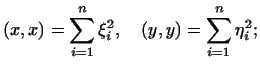 поэтому неравенство (6) имеет здесь вид:
поэтому неравенство (6) имеет здесь вид:
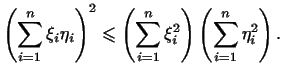
3. В примере 3 скалярное произведение имеет вид:
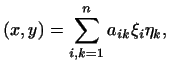 где
где
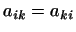 |
(2) |
и
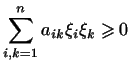 |
(3) |
для любых 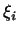 . Поэтому неравенство (6) означает: . Поэтому неравенство (6) означает:
Если числа 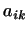 удовлетворяют условиям (2) и
(3), то имеем место неравенство удовлетворяют условиям (2) и
(3), то имеем место неравенство
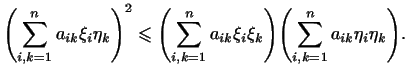
Упражнение
Показать, что если числа 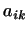 удовлетворяют условиям (2) и (3), то удовлетворяют условиям (2) и (3), то
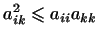 . (Указание. Выбрать в только
что выведенном неравенстве специальным образом числа . (Указание. Выбрать в только
что выведенном неравенстве специальным образом числа
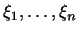 и и
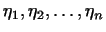 .) .)
4. В примере 4 скалярное произведение задается интегралом
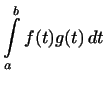 , поэтому неравенство (6)
имеет вид: , поэтому неравенство (6)
имеет вид:
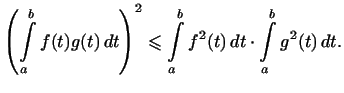 Это неравенство играет важную роль в разных вопросах анализа.
Это неравенство играет важную роль в разных вопросах анализа.
Приведем пример неравенства, являющегося следствием неравенства
Коши-Буняковского.
Для любых векторов 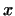 и и 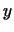 в евклидовом пространстве в евклидовом пространстве 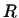 имеет
место неравенство имеет
место неравенство
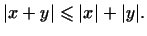 |
(7) |
Доказательство.
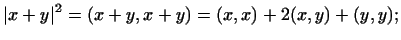 так как (в силу неравенства Коши-Буняковского)
так как (в силу неравенства Коши-Буняковского)
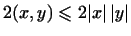 ,
то ,
то
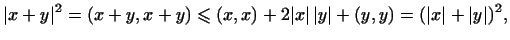 т.е.
т.е.
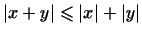 , что и требовалось доказать.
(См. также 3, стр. , что и требовалось доказать.
(См. также 3, стр.![[*]](http://images.nature.web.ru/nature/2000/10/02/0001151602/crossref.png) .) .)
Упражнение
Написать неравенство (7) в каждом из примеров евклидовых пространств,
разобранных в начале этого параграфа.
В геометрии расстояние между двумя точками 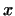 и и 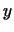 2.6определяется как длина вектора 2.6определяется как длина вектора 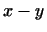 . В общем случае . В общем случае 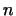 -мерного
евклидова пространства определим расстояние между -мерного
евклидова пространства определим расстояние между 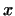 и и 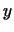 формулой
формулой
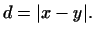




Next: 3 изоморфизм евклидовых пространств
Up: 1 n-мерное пространство. Линейные
Previous: 1 Линейное (аффинное) -мерное
Vadim Yu. Radionov
2000-08-30
Посмотреть комментарии[2]
| 
