Астрофотография и изучение движений небесных тел
2.03.1997 20:21 | Р.М. Рос/Вселенная и Мы

Астроном древних времен, вероятно, отдал бы полжизни за фотоаппарат, ибо не вызывает сомнения, что фотография гораздо точнее любого, сколь угодно хорошо выполненного, рисунка

Фотографическую камеру можно рассматривать как точный астрономический инструмент. С помощью только одного закрепленного на штативе фотоаппарата cо спусковым тросиком и достаточно чувствительной пленки можно проводить весьма интересные в дидактическом отношении астрономические наблюдения.

Остановимся на трех из многочисленных примеров, подтверждающих этот тезис, где фотографирование используется для изучения движений небесных тел, хотя, надо заметить, что его можно применять и в других исследованиях (были опубликованы десятки подобных возможностей).

Приведенные ниже примеры помогут учителю использовать астрофотографию в преподавании астрономии. Получаемые результаты, как правило, производят сильное впечатление на учеников, открывающих для себя путь в "лабораторию Вселенной", которая так манит любознательных.

Пример первый

(Рис.1. Вращение звезд вокруг Полярной звезды. Время экспозиции 35 мин, обратимя цветная плёнка, чувствительность 1000 ASA.)

Начнем с очень простого упражнения. Известные фотографии, подобные представленной на рис. 1, дают возможность оценить период вращения Земли Т. Достаточно измерить в градусах дуги центральный угол a, образованный ярким "следом" любой звезды и оценить время экспозиции t, чтобы вывести следующее соотношение:

Пример второй

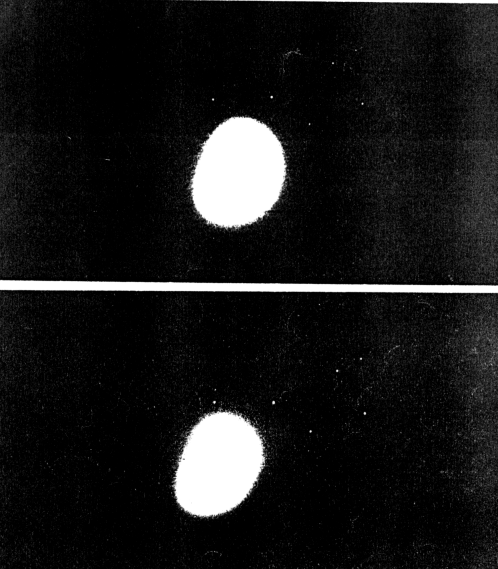
(Рис. 2. Луна в Плеядах. Камера с обьективом d=270 мм, установленная на штативе без автоматического гидирования. Черно-белая пленка с чувствительностью 400 ASA.)

Легко также вычислить период вращения Луны. Достаточно сделать два ее снимка, когда она проходит вблизи какой-либо яркой звезды. В качестве примера на рис. 2 представлены две фотографии Луны в Плеядах. Они получены с помощью 270-мм телеобъектива. Измеряя разность d положений Луны на обеих фотографиях и зная угловой ее диаметр, можно выразить полученное смещение в угловой мере. Принимая во внимание время t, прошедшее между обеими экспозициями, и переходя к соответствующим единицам измерения, получаем период обращения нашего естественного спутника:

Пример третий

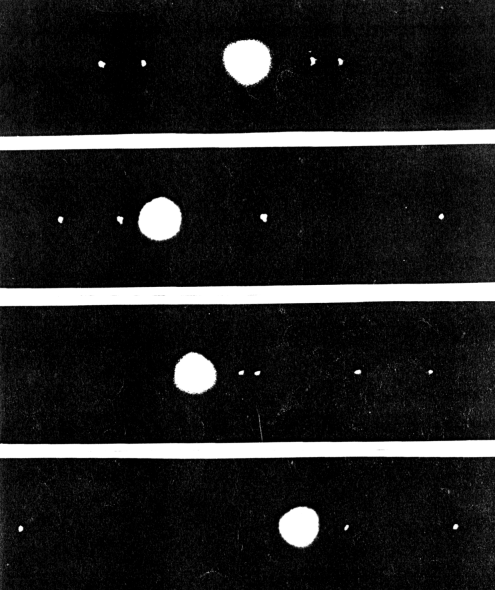
(Рис. 3. Юпитер с галилеевскими спутниками. Камера установлена на рефлекторе d= 100 мм, фокусным расстоянием 1000 мм и автоматическим гидированием. Время экспозиции 40 с, черно-белая пленка чувствительностью 400 ASA.)

Посмотрим, что можно извлечь из фотографий Галилеевых спутников Юпитера, полученных с помощью небольшого 100-мм телескопа системы Ньютона (см. примеры на рис. 3). Сравнивая истинный диаметр Юпитера 2R_J с диаметром 2r_J его изображения на фотографиях и оценивая максимальное расстояние r₀ от спутника до центра планеты по всем наблюдениям, можно получить с некоторым приближением истинное максимальное расстояние a этого спутника от центра Юпитера:

С помощью другой пропорции из рис. 4 можно получить разницу во времени наблюдений t₂ - t₁ и внутренний угол q₂ + q₁, что позволяет определить период Р обращения спутника вокруг Юпитера

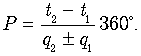
И, наконец, с помощью третьего закона Кеплера по каждому из спутников можно вычислить массу Юпитера:

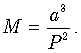
На рис. 3 приведены только три фотографии, но во время наблюдений их было получено намного больше. Полезно иметь по крайней мере одну-две дюжины снимков, сделанных через различные промежутки времени. Для изучения движения спутников Ио и Европа достаточно фотографий, полученных в течение двух последовательных ночей через 15-30 мин. Для Ганимеда и Каллисто нужно, чтобы между временем получения фотографий прошло несколько дней или даже недель.

Все фотографии, опубликованные в этой статье, были получены учениками средних школ Испании. Здесь, как на фотографиях Луны и Плеяд, так и на фотографиях Луны и ее спутников, Луна и большая планета передержаны, из-за чего их размер увеличился, а форма изменилась. Чтобы обойти эту трудность, для измерения диаметра большого светила вместо применения специальных методов мы просто использовали фотографии с другим временем экспозиции. Луна и Юпитер на них не деформированы, а Плеяды и спутники не видны.

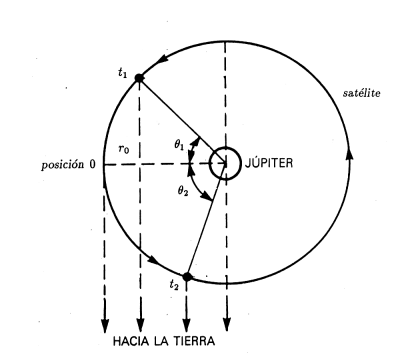
(Рис. 4. Схематическое изображение различных положений спутников Юпитера. В положениях, предшествующих или следующих за положением 0, центральный угол равен q₂-q₁, но когда первое положение предшествует, а второе следует за положением 0, центральный угол равен q₂+q₁₎

Заметим, что цель таких учебных работ - не получение точного значения различных количественных характеристик небесных тел, а демонстрация учащимся пользы от небольшого умственого усилия и некоторой изобретательности, что позволяет не просто любоваться фотографией неба как красивой картинкой, но извлечь еще из нее количественную информацию (см. табл. 1). Несомненно, было бы интересно проводить анализ ошибок, но это, к сожалению, изучают не во всех школах.

Полученные результаты являются лишь первым приближением к истине, но на большее они и не претендуют.

 

Таблица 1.

 

	Полученные значения	Истинные значения
Земля	Т = 23.3 ч	Т = 24 ч
Луна	Р = 31 день	Р = 29.5 дней
Ио	а = 6.0 RJ	а = 5.9 RJ
	Р = 1 день 11 ч	Р = 1 день 28.5 ч
Европа	а = 9.4 RJ	а = 9.4 RJ
	Р = 3 дня 18 ч	Р = 3 дня 13 ч
Ганимед	а = 15.1 RJ	а = 15.0 RJ
	Р = 6 дней 3 ч	Р = 7 дней 3.5 ч
Калисто	а = 26.3 RJ	а = 26.4 RJ
	Р= 15 дней 12 ч	Р= 16 дней 16.5 ч
Юпитер	МJ = 0.0017 М	MJ = 0.001 М

 

*)Испания, Каталонский политехнический университет. Кафедра прикладной математики и телеметрии.