Полный Архив предыдущих выпусков обзоров astro-ph.
Полезные астрономические ссылки.
Короткое эссе об электронных препринтах.
Обзорные статьи в astro-ph с 2001 г.
Авторы проекта
Сергей Попов
Михаил Прохоров
Поставьте у себя наш баннер!
Проект размещен на сайтах:
Вы может также разместить на своем сайте нашу ленту обзоров
Новости от УФН
Информнаука
Перст
25.04.2003. Начальная функция масс звезд
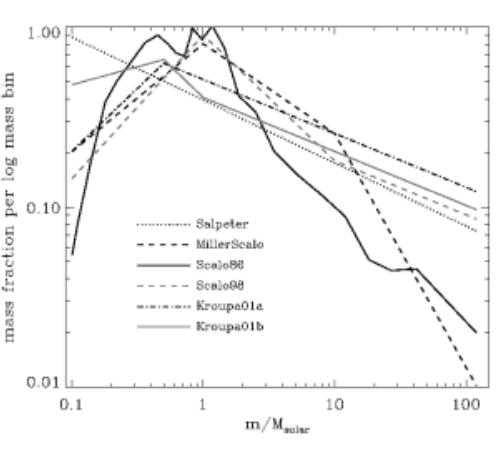
из статьи Болдри и Глэйзбрук (I. K. Baldry, K. Glazebrook)
astro-ph/0304423.
На рисунке приведены кривые (и прямые), которые описывают одну из самых важных характеристик в астрономии - звездную начальную функцию масс.
Как хорошо известно, для звезд самым главным параметром является их масса. Вообще, про одиночную звезду почти все можно сказать, зная ее возраст, массу и химический состав. Возраст данной звезды постоянно растет - звезда эволюционирует. Эволюцию одиночной звезды можно предсказать, зная оставшиеся два параметра - массу и состав. Начальный состав звезд примерно одинаков (в том смысле, что не бывает звезд из керосина или шоколада - все они состоят в основном из водорода и гелия). Разница заключается в "приправах" - до нескольких процентов элементов тяжелее гелия. Но, скажем, сейчас в нашей Галактике рождаются звезды примерно солнечного химсостава, так что даже приправлен "звездный суп" примерно одинаково. Остается масса.
Чтобы моделировать большие популяции звезд нужно знать, каковы их свойства в среднем. Самое главное - распределение по массам. Масса звезды может меняться в течение жизни (из-за звездного ветра, из-за сброса оболочки, из-за обмена масс в двойной системе). Это можно промоделировать. Главное знать, какая была масса в начале. Это и есть начальная функция масс.
Начальная функция масс (НФМ) может быть задана по-разному. Т.е. суть-то будет одна - сколько звезд каких масс - но формулу можно записать в нескольких вариантах. Это важно усвоить, чтобы понять, что нарисовано на картинке. А на ней авторы приводят несколько самых популярных функций масс. Однако, здесь мы не будем выписывать формулы (а потому не будем детально пояснять, что отложено по вертикальной оси). По горизонтальной оси отложена масса звезд. По вертикальной - доля массы в логарифмическом бине (интервале) масс. Если бы откладывали число звезд в единичном интервале масс, то кривые круче поднимались бы в сторону меньших масс.
Самая-самая популярная среди астрофизиков функция масс - солпитеровская. Еще в 1955 г. Солпитер определил, что распределение по массам хорошо описывается прямой линией в логарифмическом масштабе. Т.е. степенной функцией. Естественно, чем меньше масса, тем более многочисленны такие звезды. Солпитеровская функция масс применима к объектам с массой от 0.1 до 120 масс Солнца (на рисунке это пунктирная линия).
По сравнению с солпитеровской другие функции масс имеют завалы или на малых массах, или на больших (или и там, и там). Авторы самых известных - Скало и Крупа (см. рисунок). Функцию масс можно определять разными способами: от прямых подсчетов звезд, до использования глобальных характеристик (плюс какая-то модель). Например, можно измерить светимость галактики в разных диапазонах, и смотреть какими распределениями звезд по массам (задав модель излучения для каждой массы на каждой стадии эволюции) это можно описать. Можно определять функцию масс (особенно на маломассивном конце) по данным микролинзирования. Наконец, можно пытаться построить теоретическую кривую, моделируя процесс рождения звезд на компьютере.
Какова истина - мы не знаем. Если речь не идет об очень маломассивных объектах или наоборот о самых массивных звездах, то солпитеровская функция все хорошо описывает. Кстати, Болдри и Глэйзбрук пишут в своей работе, что в интервале масс от 0.5 до 120 масс Солнца все находится в разумном соответствии с солпитеровской функцией (по-крайней мере все можно описать одной прямой с наклоном близким к указанному в работе Солпитера 1955 г.). По всей видимости еще долго будут появляться работы, где будут находить все новые и новые свидетельства в пользу солпитеровской функции масс или в пользу Миллера-Скало, или же будут предлагать новые варианты. Хороший (но довольно специальный) обзор можно найти в работе Шабрие astro-ph/0304382. А более популярное (но вполне строгое) изложение можно найти в книге В.Г. Сурдина "Рождение звезд".