П.В. Кузьмин (Костромская Государственная Сельскохозяйственная
Академия)
Издательство КГСХА, 2002 г.
| Содержание |
Чтобы найти 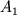 и и 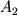 воспользуемся начальными условиями, т.е.
необходимо знать значение координаты и скорости в начальный момент времени.
Пусть воспользуемся начальными условиями, т.е.
необходимо знать значение координаты и скорости в начальный момент времени.
Пусть
Тогда с учетом этого и выражения (8) получим следующее
Откуда
Подставим постоянные интегрирования в выражение и получим. И это правильно,
т.к. решение уравнения должно быть действительным, поэтому коэффициенты
комплексно-сопряженные.
Используя представление Эйлера для комплексных чисел, и взяв только
действительную часть (именно она будет описывать реально происходящие
физические процессы), получим
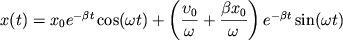 | (10) |
Выражение (10) можно привести к виду
где амплитуда - ![$X_{0} = \sqrt {\displaystyle x_{0}^{2} + \left( {{\displaystyle \frac{{\displaystyle \upsilon _{0} }}{{\displaystyle \omega }}} + {\displaystyle \frac{{\displaystyle \beta x_{0} }}{{\displaystyle \omega }}}} \right)^{2}} ,\quad \varphi _{0} = arctg\left( {\displaystyle - {\displaystyle \left[ {{\displaystyle \frac{{\displaystyle \upsilon _{0} }}{{\displaystyle \omega x_{0} }}} + {\displaystyle \frac{{\displaystyle \beta }}{{\displaystyle \omega }}}} \right]}} \right)$](http://images.nature.web.ru/nature/2002/06/10/0001187014/tex/formula163.gif) -
начальная фаза, -
начальная фаза, 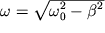 - частота
собственных затухающих колебаний. - частота
собственных затухающих колебаний.
Амплитуда и начальная фаза находятся из начальных условий для координаты и скорости, а частота собственных незатухающих колебаний и коэффициент затухания - через параметры колебательной системы (см. рис. 1.2.2).
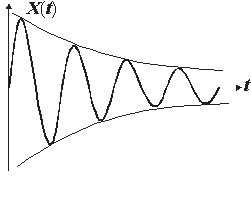 | | Рис. 1.2.2 |
Амплитуда убывает экспоненциально.
Если за некоторый промежуток времени известно изменение амплитуды, то
коэффициент затухания можно найти по формуле:
Экспоненциальная зависимость амплитуды от времени характерна только для вязкого затухания, т.е. когда сила сопротивления пропорциональна скорости движения. Факт, что вид функции затухания амплитуды связан с видом функции сопротивления, был отмечен Ньютоном.
Дополнительно для описания затухающих колебаний используется еще одна
величина.
Логарифмический декремент затухания равен натуральному логарифму отношения амплитуды колебаний в некоторый момент времени к амплитуде колебаний через один период.
Замечания о скорости и ускорении.
Скорость:
или если умножить и разделить правую часть выражения на 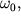 то то
Если ввести угол, определяемый условиями 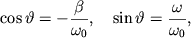 тогда: тогда:
Значение угла 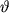 заключено в интервале заключено в интервале 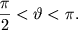 (Из каких соображений можно сделать такой вывод?) Т.о. при наличии в
системе сил сопротивления скорость опережает по фазе координату больше, чем
на (Из каких соображений можно сделать такой вывод?) Т.о. при наличии в
системе сил сопротивления скорость опережает по фазе координату больше, чем
на 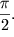
Ускорение.
Проделывая ту же процедуру, что и раньше, получим
т.е. ускорение опережает скорость также на угол 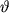 , который изменяется от , который изменяется от
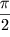 до до 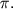
Если 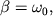 тогда говорят о критическом затухании. Если подставить значения
коэффициента затухания и собственной частоты колебаний, то для величины
критического затухания получим тогда говорят о критическом затухании. Если подставить значения
коэффициента затухания и собственной частоты колебаний, то для величины
критического затухания получим
Решение уравнения (7) будет иметь вид:
где 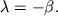
Рассмотрим, например, незатухающие колебания крутильного маятника. За
координату выберем угол поворота. Возвращающая сила при больших отклонениях
(при больших углах поворота) от положения равновесия не является линейной.
Запишем уравнение движения, составленное по 2-му закону Ньютона для
вращательного движения.
Момент, действующий на маятник, является некоторой функцией угла поворота.
знак минус говорит о том, что момент является возвращающим, т.е. действует в
направлении противоположном смещению из положения равновесия. Тогда
Введем обозначение 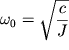 (частота собственных незатухающих колебаний или
собственная частота), окончательно приведем к виду: (частота собственных незатухающих колебаний или
собственная частота), окончательно приведем к виду:
Вторую производную по времени преобразуем к виду
Тогда уравнение движения принимает вид
Предполагая, что маятник находится в положении максимального удаления от
положения равновесия, получим
Это означает, что для любого положения колеблющегося маятника его
кинетическая энергия равна разности накопленной (максимальной) потенциальной
энергии и потенциальной энергии в рассматриваемый момент времени.
Выразим
Знак минус принят потому, что в рассматриваемых начальных условиях угол
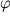 с течением времени убывает. с течением времени убывает.
Интегрируя, получаем
Откуда можно вычислить время, необходимое для достижения маятником любого
заданного положения.
Назад| Вперед
Написать комментарий
| 
