Научная Сеть >> Колебания. Краткий конспект лекций.

Наука >> Физика >> Общая физика >> Колебания и волны >> Электрические колебания | Курсы лекций

Написать комментарий

Добавить новое сообщение

См. также

Б.А. Бахметев дипломат, политик, мыслитель

Колебания. Краткий конспект лекций.

П.В. Кузьмин (Костромская Государственная Сельскохозяйственная Академия)
Издательство КГСХА, 2002 г.

Содержание

7. Вынужденные электромагнитные колебания

7.1. Вынужденные электромагнитные колебания в идеальном электрическом контуре

При наличии источника изменяющейся ЭДС уравнение для идеального электрического контура примет вид (схема 3):

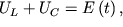$U_{L} + U_{C} = E\left( {\displaystyle t} \right),$

(49)

Если ЭДС изменяется по гармоническому закону, тогда из (49) получим

$L{\displaystyle \frac{{\displaystyle dI}}{{\displaystyle dt}}} + {\displaystyle \frac{{\displaystyle q}}{{\displaystyle C}}} = E_{0} \cos \left( {\displaystyle \Omega t + \theta } \right)\quad или \quad {\displaystyle \frac{{\displaystyle d^{2}q}}{{\displaystyle dt^{2}}}} + \omega _{0}^{2} q = {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle L}}}\cos \left( {\displaystyle \Omega t + \theta } \right)$

(50)

Выражение (50) - это дифференциальное уравнение вынужденных гармонических незатухающих колебаний в электрическом контуре.

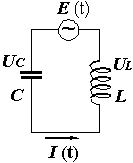Схема 3

Решение (см. п. 2.1.) уравнения (50) имеет вид:

1. Случай отсутствия резонанса. (условие 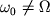$\omega _{0} \ne \Omega$ )

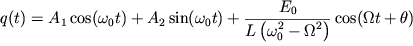$q(t) = A_{1} \cos (\omega _{0} t) + A_{2} \sin (\omega _{0} t) + {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle L\left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)}}}\cos (\Omega t + \theta )$

(51)

Выражение (51) можно привести к виду

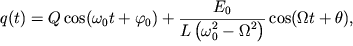$q(t) = Q\cos (\omega _{0} t + \varphi _{0} ) + {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle L\left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)}}}\cos (\Omega t + \theta ),$

(52)

где амплитуда заряда и начальная фаза:

$Q = \sqrt {\displaystyle A_{1}^{2} + A_{2}^{2} } ,{\displaystyle \begin{array}{*{20}c} {\displaystyle } \hfill & {\displaystyle } \hfill \\ \end{array} }\varphi _{0} = arctg\left( {\displaystyle - {\displaystyle \frac{{\displaystyle A_{2} }}{{\displaystyle A_{1} }}}} \right).$

Амплитуда и начальная фаза колебаний при действии вынуждающей силы (ЭДС) зависят не только от начальных условий, но и от параметров возмущающей силы (ЭДС).

В зависимости от соотношения между частотами при вынужденных колебаниях в электрическом контуре возможно возникновение биений и явления резонанса. (см. п. 2.1.)

2. Случай, когда частота вынуждающей силы близка, но отличается от собственной частоты колебаний системы.(условие 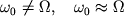$\omega _{0} \ne \Omega , \quad \omega _{0} \approx \Omega$ )

Сложение собственных сопровождающих и вынужденных колебаний приводит к биениям в результате наложения сопровождающих и вынужденных колебаний.

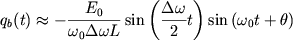$q_{b} (t) \approx - {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle \omega _{0} \Delta \omega L}}}\sin \left( {{\displaystyle \frac{{\displaystyle \Delta \omega }}{{\displaystyle 2}}}t} \right)\sin \left( {\displaystyle \omega _{0} t + \theta } \right)$

(53)

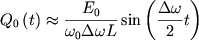где $Q_{0} \left( {\displaystyle t} \right) \approx {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle \omega _{0} \Delta \omega L}}}\sin \left( {{\displaystyle \frac{{\displaystyle \Delta \omega }}{{\displaystyle 2}}}t} \right)$ - амплитуда биений.

Частота биений 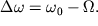$\Delta \omega = \omega _{0} - \Omega .$ Амплитуда биений является периодической медленно изменяющейся функцией времени.

Полное решение в случае биений принимает вид:

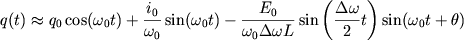$q(t) \approx q_{0} \cos (\omega _{0} t) + {\displaystyle \frac{{\displaystyle i_{0} }}{{\displaystyle \omega _{0} }}}\sin (\omega _{0} t) - {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle \omega _{0} \Delta \omega L}}}\sin \left( {{\displaystyle \frac{{\displaystyle \Delta \omega }}{{\displaystyle 2}}}t} \right)\sin (\omega _{0} t + \theta )$

(54)

(собственные колебания "остаются" и "происходят также как и раньше сами собой").

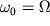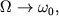3. Случай резонанса. ( условие $\omega _{0} = \Omega$ ) В выражении (23) переходим к пределу $\Omega \to \omega _{0} ,$ тогда

$q_{res} (t) \approx - {\displaystyle \mathop {\displaystyle \lim }\limits_{\Omega \to \omega _{0} } }{\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle \omega _{0} \Delta \omega L}}}\sin \left( {{\displaystyle \frac{{\displaystyle \Delta \omega }}{{\displaystyle 2}}}t} \right)\sin \left( {\displaystyle \omega _{0} t + \theta } \right)$

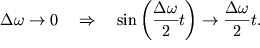При этом $\Delta \omega \to 0\quad \Rightarrow \quad \sin \left( {{\displaystyle \frac{{\displaystyle \Delta \omega }}{{\displaystyle 2}}}t} \right) \to {\displaystyle \frac{{\displaystyle \Delta \omega }}{{\displaystyle 2}}}t.$ Тогда

$q_{res} (t) \approx - {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle \omega _{0} \Delta \omega L}}}{\displaystyle \frac{{\displaystyle \Delta \omega }}{{\displaystyle 2}}}t \cdot \sin \left( {\displaystyle \omega _{0} t + \theta } \right)$

и окончательно получаем

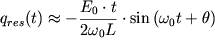$q_{res} (t) \approx - {\displaystyle \frac{{\displaystyle E_{0} \cdot t}}{{\displaystyle 2\omega _{0} L}}} \cdot \sin \left( {\displaystyle \omega _{0} t + \theta } \right)$

(55)

Вывод: Колебания происходят с собственной частотой и амплитудой, линейно возрастающей с течением времени. [С.П. Тимошенко, 1959]

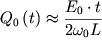$Q_{0} \left( {\displaystyle t} \right) \approx {\displaystyle \frac{{\displaystyle E_{0} \cdot t}}{{\displaystyle 2\omega _{0} L}}}$ - амплитуда при резонансе как функция времени.

Поскольку затухание отсутствует, то амплитуда колебаний возрастает до бесконечности, что приводит к разрушению системы.

7.2. Вынужденные электромагнитные колебания в реальном электрическом контуре

При наличии источника изменяющейся ЭДС уравнение для реального последовательного электрического контура примет вид:

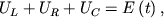$U_{L} + U_{R} + U_{C} = E\left( {\displaystyle t} \right),$

(56)

Если ЭДС изменяется по гармоническому закону, тогда из (56) получим

$L{\displaystyle \frac{{\displaystyle dI}}{{\displaystyle dt}}} + R \cdot I + {\displaystyle \frac{{\displaystyle q}}{{\displaystyle C}}} = E_{0} \cos \left( {\displaystyle \Omega t + \theta } \right)$

или

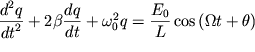${\displaystyle \frac{{\displaystyle d^{2}q}}{{\displaystyle dt^{2}}}} + 2\beta {\displaystyle \frac{{\displaystyle dq}}{{\displaystyle dt}}} + \omega _{0}^{2} q = {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle L}}}\cos \left( {\displaystyle \Omega t + \theta } \right)$

(57)

Выражение (57) - это дифференциальное уравнение вынужденных гармонических колебаний в реальном электрическом контуре.

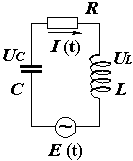Схема 4

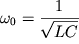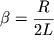где $\omega _{0} = {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \sqrt {\displaystyle LC} }}}$ - частота собственных незатухающих колебаний и $\beta = {\displaystyle \frac{{\displaystyle R}}{{\displaystyle 2L}}}$ - коэффициент затухания.

Решение (см. п. 2.1.) уравнения (54) имеет вид

$q\left( {\displaystyle t} \right) = A_{1} e^{ - \beta t}\cos \omega t + A_{2} e^{ - \beta t}\sin \omega t + {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle L\sqrt {{\displaystyle \left[ {\displaystyle \left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)^{2} + 4\beta ^{2}\Omega ^{2}} \right]}} }}}\cos \left( {\displaystyle \Omega t + \theta + \varepsilon } \right)$

(58)

Выражение (58) принимает вид (см. п. 2.2.):

$q(t) = \left( {\displaystyle q_{0} - {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle L\sqrt {{\displaystyle \left[ {\displaystyle \left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)^{2} + 4\beta ^{2}\Omega ^{2}} \right]}} }}}\cos \left( {\displaystyle \theta + \varepsilon } \right)} \right) \cdot e^{ - \beta t}\cos \omega t + \left( {{\displaystyle \frac{{\displaystyle i_{0} + \beta q_{0} }}{{\displaystyle \omega }}} + {\displaystyle \frac{{\displaystyle \Omega E_{0} \sin \left( {\displaystyle \theta + \varepsilon } \right) - \beta E_{0} \cos \left( {\displaystyle \theta + \varepsilon } \right)}}{{\displaystyle \omega \cdot L\sqrt {{\displaystyle \left[ {\displaystyle \left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)^{2} + 4\beta ^{2}\Omega ^{2}} \right]}} }}}} \right) \cdot e^{ - \beta t}\sin \omega t + {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle L\sqrt {{\displaystyle \left[ {\displaystyle \left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)^{2} + 4\beta ^{2}\Omega ^{2}} \right]}} }}}\cos (\Omega t + \theta + \varepsilon )$

(59)

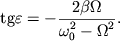Значение фазы $\varepsilon$ вынужденных колебаний ${\displaystyle \rm tg}\varepsilon = - {\displaystyle \frac{{\displaystyle 2\beta \Omega }}{{\displaystyle \omega _{0}^{2} - \Omega ^{2}}}}.$ См. выражения (30) - (31).

Рассмотрим установившиеся вынужденные колебания. (Последнее слагаемое.)

(Аналогия между механическими и электромагнитными колебаниями: координата - заряд, скорость - сила тока.) Изменение заряда имеет вид:

$q_{уст} \left( {\displaystyle t} \right) = {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle L\sqrt {{\displaystyle \left[ {\displaystyle \left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)^{2} + 4\beta ^{2}\Omega ^{2}} \right]}} }}}\cos \left( {\displaystyle \Omega t + \theta + \varepsilon } \right),$

где $Q_{0} = {\displaystyle \frac{{\displaystyle E_{0} }}{{\displaystyle L\sqrt {{\displaystyle \left[ {\displaystyle \left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)^{2} + 4\beta ^{2}\Omega ^{2}} \right]}} }}}$ - амплитуда вынужденных колебаний заряда.

Изменение силы тока (сила тока производная заряда по времени):

$I\left( {\displaystyle t} \right) = - {\displaystyle \frac{{\displaystyle \Omega E_{0} }}{{\displaystyle L\sqrt {{\displaystyle \left[ {\displaystyle \left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)^{2} + 4\beta ^{2}\Omega ^{2}} \right]}} }}}\sin \left( {\displaystyle \Omega t + \theta + \varepsilon } \right),$

(60)

где

$I_{0} = {\displaystyle \frac{{\displaystyle \Omega E_{0} }}{{\displaystyle L\sqrt {{\displaystyle \left[ {\displaystyle \left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)^{2} + 4\beta ^{2}\Omega ^{2}} \right]}} }}} = \Omega Q_{0}$

(61)

амплитуда силы тока при вынужденных колебаниях. [И.В. Савельев, 1982]

Найдем значение частоты вынуждающей силы, при которой достигается максимальное значение амплитуды силы тока в цепи

${\displaystyle \frac{{\displaystyle dI_{0} }}{{\displaystyle d\Omega }}} = {\displaystyle \frac{{\displaystyle d}}{{\displaystyle d\Omega }}}\left( {{\displaystyle \frac{{\displaystyle \Omega E_{0} }}{{\displaystyle L\sqrt {{\displaystyle \left[ {\displaystyle \left( {\displaystyle \omega _{0}^{2} - \Omega ^{2}} \right)^{2} + 4\beta ^{2}\Omega ^{2}} \right]}} }}}} \right) = 0$

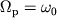Откуда $\Omega _{р} = \omega _{0}$ (рис. 7.2.1).

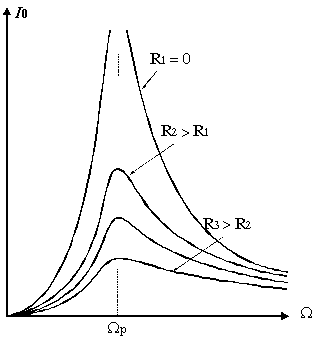Рис. 7.2.1

Назад| Вперед

П.В.Кузьмин

Написать комментарий