Next: 4 Задачи на повторение
Up: Тригонометрия для абитуриентов
Previous: 2 Отбор чисел на
Повторить:п. 2.2. Определение тригонометрических функций.
п. 2.7. Графики синуса и косинуса.
Мы начнем с простейших
неравенств, к которым
любое тригонометрическое неравенство в конечном счете сводится.
Пример 3.1
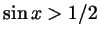 . .
Рис. 104:
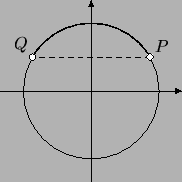 |
Решение. Для начала выясним, какие точки на
тригонометрической окружности соответствуют решениям
неравенства. Это - точки, ордината которых больше 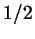 , и на
окружности они заполняют дугу , и на
окружности они заполняют дугу 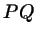 , отмеченную на
рис. 104. , отмеченную на
рис. 104.
Теперь можно записать множество чисел, соответствующих точкам на
дуге 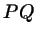 . Ясно, что это множество содержит интервал . Ясно, что это множество содержит интервал
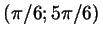 ( (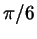 соответствует точке соответствует точке 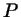 , , 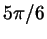 -
точке -
точке 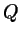 ), а вообще наше множество состоит из всех интервалов ), а вообще наше множество состоит из всех интервалов
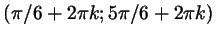 , где , где 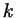 - целое: ведь если
точке на тригонометрической окружности соответствует число - целое: ведь если
точке на тригонометрической окружности соответствует число 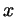 ,
то ей же соответствуют и все числа вида ,
то ей же соответствуют и все числа вида 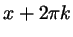 ( (
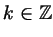 )
(рис. 105). )
(рис. 105).
Рис. 105:
 |
Ответ к неравенству можно записать так:
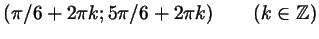 или еще проще:
или еще проще:
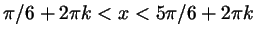 . .
Пример 3.2
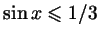 . .
Рис. 106:
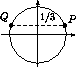 |
Решение. На тригонометрической окружности множество
решений неравенства изобразится дугой 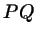 , отмеченной на
рис. 106. Нам нужно выбрать на числовой оси какой-нибудь
отрезок, соответствующий этой дуге, и тогда останется только
прибавить к его границам , отмеченной на
рис. 106. Нам нужно выбрать на числовой оси какой-нибудь
отрезок, соответствующий этой дуге, и тогда останется только
прибавить к его границам 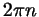 .
Выберем какое-нибудь число, соответствующее одному из концов
дуги. Очевидно, точке .
Выберем какое-нибудь число, соответствующее одному из концов
дуги. Очевидно, точке 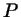 соответствует соответствует
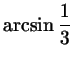 . Раз
это число выбрано, выбор числа, соответствующего другому концу,
уже предопределен. Чтобы найти это число, надо сдвинуться из
точки . Раз
это число выбрано, выбор числа, соответствующего другому концу,
уже предопределен. Чтобы найти это число, надо сдвинуться из
точки
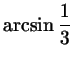 на числовой оси в отрицательном
направлении на расстояние, равное длине дуги на числовой оси в отрицательном
направлении на расстояние, равное длине дуги 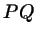 . Точке . Точке 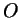 на
окружности соответствует ноль, точке на
окружности соответствует ноль, точке 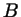 - число - число 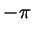 , а
точке , а
точке 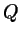 - число, расположенное еще на - число, расположенное еще на
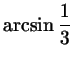 левее, то есть
левее, то есть
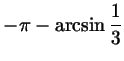 . Стало быть, один из
отрезков, соответствующих дуге . Стало быть, один из
отрезков, соответствующих дуге 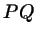 , будет , будет
![$ \Bigl[-\pi-\arcsin\dfrac13; \arcsin\dfrac13\Bigr]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s5img422.gif) , а ответом к
неравенству , а ответом к
неравенству
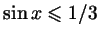 будет объединение отрезков будет объединение отрезков
![$\displaystyle \Bigl[-\pi-\arcsin\dfrac13+2\pi k; \arcsin\dfrac13+2\pi k\Bigr]\quad
(k\in\mathbb{Z}).
$](http://images.nature.web.ru/nature/2000/12/28/0001158396//s5img423.preview.gif) Разумеется, тот же ответ можно представить и по-иному, например
Разумеется, тот же ответ можно представить и по-иному, например
![$\displaystyle \Bigl[-\dfrac\pi2 +2\pi k; \arcsin\dfrac13+2\pi k\Bigr];\quad
\Bigl[\pi-\arcsin\dfrac13+2\pi k; \dfrac{3\pi}2+ 2\pi k\Bigr].
$](http://images.nature.web.ru/nature/2000/12/28/0001158396//s5img424.preview.gif)
Рис. 107:
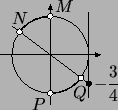 |
Пример 3.3
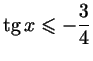 . .
Решение. Используя ось тангенсов, легко убедиться, что
на тригонометрической окружности
решения неравенства изображаются двумя дугами, отмеченными на рис. 107.
Дуге 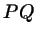 соответствует интервал соответствует интервал
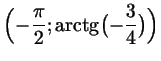 , а дуге , а дуге 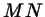 - интервал - интервал
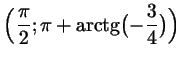 .
Второй из этих интервалов получается из
первого сдвигом на .
Второй из этих интервалов получается из
первого сдвигом на 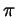 , так что ясно, что ответ к неравенству
- это объединение интервалов , так что ясно, что ответ к неравенству
- это объединение интервалов
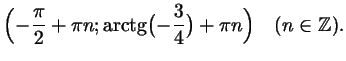 При решении простейших тригонометрических неравенств можно также
пользоваться не тригонометрическим кругом, а графиками. Например,
чтобы решить то же неравенство
При решении простейших тригонометрических неравенств можно также
пользоваться не тригонометрическим кругом, а графиками. Например,
чтобы решить то же неравенство
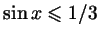 , достаточно
отметить на числовой оси такие точки, что лежащие над ними точки
графика , достаточно
отметить на числовой оси такие точки, что лежащие над ними точки
графика
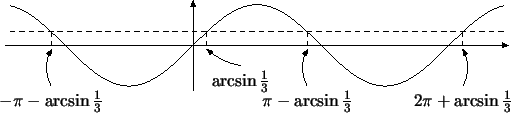
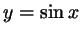 имеют ординату не более имеют ординату не более 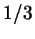 (рис. 108).
По этому рисунку легко записать ответ.
(рис. 108).
По этому рисунку легко записать ответ.
Рис. 108:
 |
При оформлении решений простейших тригонометрических неравенств
не надо записывать рассуждений наподобие тех, что мы проводили в
этих примерах: достаточно рисунка наподобие рис. 106 и
ответа. Можно также нарисовать рисунок наподобие
рис. 108 и опять же записать ответ.
Задача 3.1
Решите неравенства:
а)
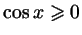 ;
б) ;
б)
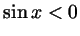 ;
в) ;
в)
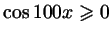 ;
г) ;
г)
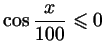 ;
д) ;
д)
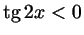 . .
Задача 3.2
Решите неравенства:
а)
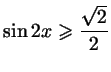 ;
б) ;
б)
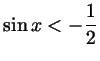 ;
в) ;
в)
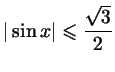 ;
г) ;
г)
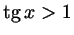 ;
д) ;
д)
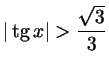 . .
Задача 3.3
Решите неравенства:
а)
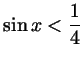 ;
б) ;
б)
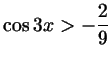 ;
в) ;
в)
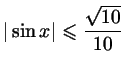 . .
Задача 3.4
Решите неравенства:
а)
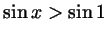 ;
б) ;
б)
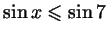 ;
в) ;
в)
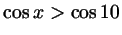 . .
Задача 3.5
Решите неравенства:
а)
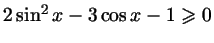 ;
б) ;
б)
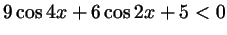 ;
в) ;
в)
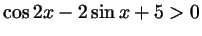 . .
Задача 3.6
Решите неравенства:
а)
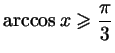 ;
б) ;
б)
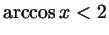 ; ;
в)
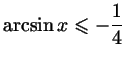 ;
г) ;
г)
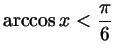 . .
Приведем пример решения более сложного неравенства.
Пример 3.4
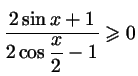 . .
Решение. Мы применим
``метод интервалов'', который должен
быть вам знаком по решению рациональных неравенств. Рецепт таков:
надо на числовой оси отметить те точки, в которых обращаются
в нуль числитель и знаменатель; на каждом из интервалов, на
которые делится этими точками числовая ось, знак левой части
будет постоянен, и останется только записать ответ как
объединение интервалов с нужным знаком. В случае
тригонометрических неравенств точек и интервалов будет, как
правило, бесконечно много, однако они будут периодически
повторяться, поэтому достаточно все проделать на отрезке длиной в
период.
В нашем случае наименьшим периодом числителя будет 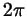 , а
знаменателя , а
знаменателя 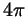 . Будем поэтому рассматривать знак левой части
на отрезке . Будем поэтому рассматривать знак левой части
на отрезке ![$ [0;4\pi]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s5img458.gif) : его длина равна : его длина равна 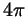 , а это число служит
периодом как числителя, так и знаменателя. , а это число служит
периодом как числителя, так и знаменателя.
Легко видеть, что на отрезке ![$ [0;4\pi]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s5img458.gif) числитель обращается в
нуль в точках числитель обращается в
нуль в точках
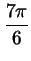 , ,
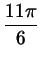 , ,
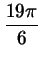 и
и
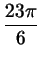 , а знаменатель - в точках , а знаменатель - в точках
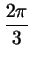 и и
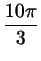 . Знаки числителя, знаменателя и левой части
удобно записать в таблице (точки, в которых знаменатель
обращается в нуль, мы в интервалы не включили). . Знаки числителя, знаменателя и левой части
удобно записать в таблице (точки, в которых знаменатель
обращается в нуль, мы в интервалы не включили).
Теперь, выделяя промежутки, на которых левая часть
неотрицательна, и прибавляя к их концам 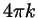 , получаем , получаем
Ответ:
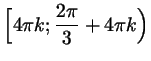 ; ;
![$ \Bigl[\dfrac{7\pi}6+4\pi k;\dfrac{11\pi}6+4\pi k\Bigr]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s5img478.gif) ; ;
![$ \Bigl[\dfrac{19\pi}6+4\pi k;\dfrac{10\pi}3+4\pi k\Bigr]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s5img479.gif) ; ;
![$ \Bigl[\dfrac{23\pi}6+4\pi k;4\pi +4\pi k\Bigr]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s5img480.gif) ( (
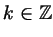 ). ).
Задача 3.7
Ответ к неравенству из примера 0.20 можно записать
и так:
![$ \Bigl[\dfrac{7\pi}6+4\pi k;\dfrac{11\pi}6+4\pi k\Bigr]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s5img478.gif) ; ;
![$ \Bigl[\dfrac{19\pi}6+4\pi k;\dfrac{10\pi}3+4\pi k\Bigr]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s5img479.gif) ; ;
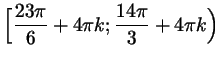 (
(
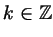 ).
Убедитесь, что ответ в этой форме задает то же самое множество
значений ).
Убедитесь, что ответ в этой форме задает то же самое множество
значений 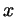 . .
Задача 3.8
Решите неравенства:
а)
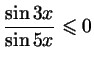 ;
б) ;
б)
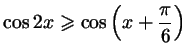 ;
в) ;
в)
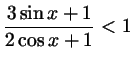 . .
Написать комментарий
|

