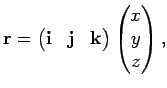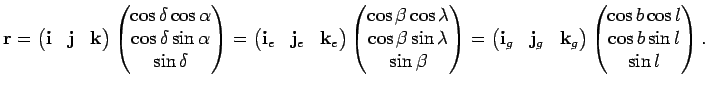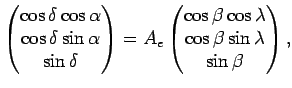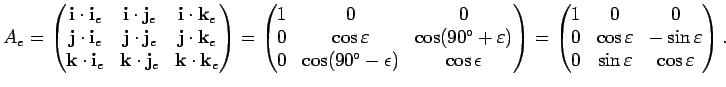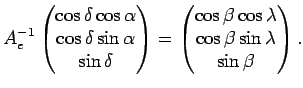<< 3.4. Галактическая система координат
| Оглавление |
3.6. Суточное вращение небесной >>
3.5. Преобразование координат из одной системы в другую
Данная задача уже упоминалась при рассмотрении горизонтальной системы координат. Если система установки телескопа горизонтальная, то движение звезд в этой системе будет неравномерным. Для точного ведения телескопа за звездой требуется непрерывно пересчитывать экваториальные координаты звезды в горизонтальные.
Рассмотрим сначала классический метод и найдем выражения, связывающие экваториальные и горизонтальные координаты. Затем рассмотрим матричный метод, который значительно облегчает задачу преобразования координат вектора из одной системы в другую.
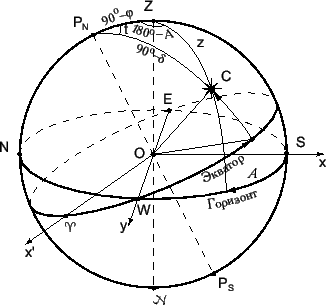
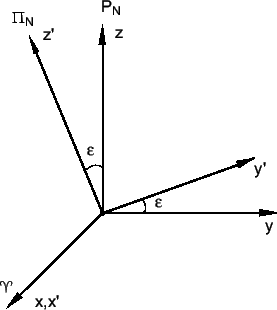
Рассмотрим треугольник 
(рис. 3.6).
. Такой треугольник называется параллактическим.
Согласно определениям координат, имеем: дуга
равна зенитному расстоянию 
, дуга
равна
, дуга
равна
, двугранный угол 
- это часовой угол
, двугранный угол равен
. Допустим, что
требуется найти зенитное расстояние и азимут источника по его
сферическим координатам. По теореме косинусов, используя
треугольник , имеем:
По теореме синусов получим:
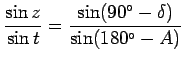
По теореме подобия получим:
Из системы уравнений (3.1-3.3) можно однозначно определить
и 
по координатам 
и . Обратим внимание на
необходимость использования всех трех уравнений (3.1-3.3)
для решения задачи. Так как азимут входит в уравнения под
знаком синуса и косинуса, то только совместное решение
уравнений (3.2-3.3) позволяет однозначно найти .
Обратное преобразование (от и к и ) можно
записать в виде:
Точно так же можно получить формулы, связывающие экваториальную систему координат с эклиптической, экваториальную с галактической и т.д.
Однако более просто найти преобразование от одной системы координат к другой системе с помощью матричных методов. Так как в дальнейшем мы будем использовать эти методы часто, рассмотрим их подробно.
Разложение вектора по тройке базисных векторов (
, 
,
) было записано в виде (2.5):
, 
, - проекции вектора 
(2.3) на
векторы 
, 
, 
, соответственно.
Используя матричные обозначения, это выражение можно записать в
виде:
где запись (
) обозначает
вектор-строку. Оставим обозначение (
)
для базисной тройки векторов экваториальной системы. Базисные
тройки векторов эклиптической и галактической системы координат
обозначены в § 3.3 и 3.4 как (
) и (
), соответственно.
Разложим радиус-вектор одного и того же небесного объекта по
базисным тройкам экваториальной, эклиптической и галактической
систем. Для этого используем формулу (2.20), в которой
координаты
заменяются на
, или
, или 
, и запишем матричное
равенство (3.5) в виде:
Чтобы найти преобразование от одной системы координат к другой, надо найти матрицу поворота от одной базисной тройки к другой. Например, найдем преобразование от экваториальной к эклиптической системе. Тогда
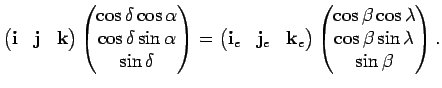
Умножим обе части уравнения на вектор-столбец
слева, где индекс
"T" обозначает транспонирование, т.е.
.
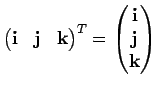В результате получим
- единичная матрица.
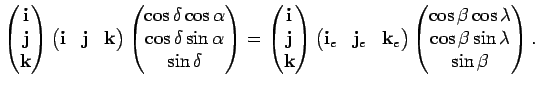
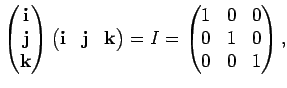
Таким образом преобразование от эклиптической к экваториальной системе можно записать следующим образом:
где
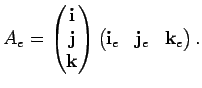
Вычислим матрицу 
в явном виде, используя рис. 3.7.
направлена в точку весеннего
равноденствия 
. Поэтому направление векторов и
совпадает. Оси 
и 
направлены соответственно
в полюс мира 
и полюс эклиптики 
. Следовательно угол
между векторами и 
равен
. Угол
между векторами и 
также равен
.
Используя определение скалярного произведения, получим:
Уравнения (3.7) и (3.8) однозначно определяют связь между двумя системами координат, и удобны при вычислении на компьютере. Тем не менее приведем преобразование (3.7) в явном виде:
Используя матричную запись (3.7) легко найти обратное преобразование от экваториальной к эклиптической системе координат. Для этого умножим уравнение (3.7) слева на матрицу, обратную
, т.е. на 
:
Матрица
обладает специальными свойствами. Нетрудно проверить,
что
, т.е.
.
Подобные матрицы называются
ортогональными. П