В 1834 году шотландский инженер-кораблестроитель и ученый Дж. Рассел, наблюдая за движением баржи по
каналу, которую тащила пара лошадей, обратил внимание на удивительное
явление. При внезапной остановке судна масса воды вокруг баржи в узком
канале не остановилась, а собралась около носа судна, и затем оторвалась от
него и в виде большого уединенного водного холма стала двигаться со
скоростью около 8 миль в час. Удивительно, что форма холма в процессе его
движения практически не менялась. Рассел назвал это движущееся по
поверхности воды образование "great solitary wave", что в переводе
означает "большая уединенная волна".
Теоретическое объяснение уединенные волны получили впоследствии в работах
французского ученого Ж. В. де Буссинеска и английского физика Дж. Рэлея. Они
обосновали математически возможность существования уединенных волн в
мелководных каналах.
После смерти Рассела в 1895 году голландский физик Д. Кортевег и его ученик
Г. де Фрис вывели уравнение, описывающее уединенные волны. Это уравнение
получило название уравнения Кортевега - де Фриса (уравнение КДФ) и имеет
вид
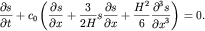 | (6.65) |
Оно описывает распространение поверхностных гравитационных волн на мелкой
воде. Здесь 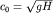 - скорость волн мелкой воды, - скорость волн мелкой воды, 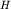 - глубина
водоема. Отметим сразу, что по виду уравнение КДФ отличается от нелинейного
уравнения (6.50) наличием дополнительного члена - глубина
водоема. Отметим сразу, что по виду уравнение КДФ отличается от нелинейного
уравнения (6.50) наличием дополнительного члена
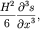 ответственного за дисперсию гравитационных волн (хотя и небольшую на мелкой
воде).
ответственного за дисперсию гравитационных волн (хотя и небольшую на мелкой
воде).
Рассмотрим несколько подробнее влияние нелинейности и дисперсии на
распространение поверхностных гравитационных волн. По аналогии с нелинейными
акустическими волнами сразу можем сказать, что скорость различных участков
поверхностной волны будет различна:
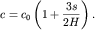 | (6.66) |
Из-за различия скоростей (гребень волны движется быстрее впадины) происходит
превращение гармонической волны в пилообразную. Крутой фронт под действием
силы тяжести опрокидывается, и на поверхности воды появляются пенистые
гребешки. Опрокидывание фронта легко наблюдать при движении волны по
мелководью вблизи берега (рис. 6.12). Однако в ряде случаев нелинейное
искажение волны может компенсироваться дисперсией. В самом деле,
пилообразная волна представляет собой набор гармонических волн с разными
частотами. Из-за дисперсии эти волны движутся с разными скоростями, и
поэтому пилообразный фрагмент волны, подобно импульсу, стремится
расшириться. При определенной форме фрагмента оба конкурирующих механизма
могут компенсировать друг друга, и тогда по поверхности воды побежит
устойчивая структура в виде уединенной волны (солитона). Выясним некоторые
свойства этой уединенной волны.
 | | Рис. 6.12. |
Предположим, что солитон имеет амплитуду 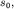 протяженность вдоль оси
Ox, равную протяженность вдоль оси
Ox, равную 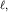 и представляет собой некоторый холмик, изображенный на
рисунке 6.13. Оценим величины нелинейного и дисперсионного членов в
уравнении КДФ: и представляет собой некоторый холмик, изображенный на
рисунке 6.13. Оценим величины нелинейного и дисперсионного членов в
уравнении КДФ:
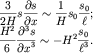 | (6.67) |
В (6.67) учтено, что на переднем и заднем фронтах холмика 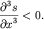 Естественно, что оба механизма будут
компенсировать друг друга при условии Естественно, что оба механизма будут
компенсировать друг друга при условии
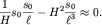 | (6.68) |
Последнее накладывает связь на амплитуду 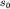 и длину и длину  солитона: солитона:
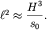 | (6.69) |
Таким образом, чем больше амплитуда солитона 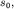 тем меньше должна быть
его длина тем меньше должна быть
его длина 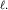 Скорость солитона c возрастает с ростом амплитуды, что
характерно для нелинейного распространения волн. Скорость солитона c возрастает с ростом амплитуды, что
характерно для нелинейного распространения волн.
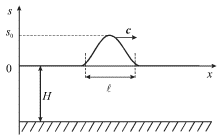 | | Рис. 6.13. |
Точное решение уравнения КДФ, описывающее солитон, имеет вид
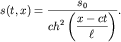 | (6.70) |
При этом длина солитона  связана с амплитудой связана с амплитудой 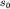 соотношением соотношением
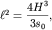 | (6.71) |
а скорость
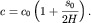 | (6.72) |
Если 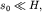 то последнее выражение можно переписать в виде то последнее выражение можно переписать в виде
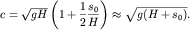 | (6.73) |
Эту формулу мы уже записывали при качественном обсуждении поведения
гравитационных волн по мере их приближения к берегу.
Важно подчеркнуть, что солитон является устойчивой структурой. Если
первоначально соотношение (6.71) не выполняется и амплитуда 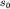 слишком
велика, то водяной холм распадается на несколько меньших холмиков, из
которых сформируются солитоны. Напротив, если слишком
велика, то водяной холм распадается на несколько меньших холмиков, из
которых сформируются солитоны. Напротив, если 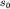 слишком мала, то такой
низкий холм расползется вследствие дисперсии. слишком мала, то такой
низкий холм расползется вследствие дисперсии.
По современным представлениям большинство волн цунами образуются, когда
достаточно крупный, но безвредный в океане солитон выбрасывается на берег.
При подходе к берегу он становится выше и короче, и его высота становится
сравнима с глубиной океана вблизи берега.
В заключение этой темы отметим, что в настоящее время обнаружены солитоны
для волн различной природы. Так, например, существуют солитоны при
распространении акустических волн в кристаллах, световых импульсов в
волоконных световодах, ионно-звуковых волн в плазме и др. Во всех случаях
существование солитонов обусловлено взаимной компенсацией нелинейных и
дисперсионных эффектов. Естественно, что энергия, переносимая уединенной
волной любой природы, будет диссипировать в тепло, поэтому по мере
распространения амплитуда солитона будет стремиться уменьшиться, что,
естественно, рано или поздно приведет к его исчезновению.
Назад
Посмотреть комментарии[2]
| 
