<< 8. Уравнение движения в
| Оглавление |
Рекомендуемая и цитируемая литература >>
Разделы
Уравнение гравитационного поля в ньютоновской механике хорошо известно.
Гравитационная сила, действующая со стороны точечной массы 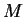 на пробную
частицу массы на пробную
частицу массы 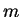 , расположенную на расстоянии , расположенную на расстоянии 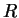 от этого тела,
представляется как: от этого тела,
представляется как:
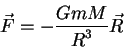
Гравитационную силу от произвольного распределения масс можно получить взяв
интеграл по плотности. Однако, чаще в теоретической физике вводят понятие
гравитационного потенциала 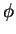 , с помощью которого уже вычисляют
гравитационную силу действующую на пробную частицу: , с помощью которого уже вычисляют
гравитационную силу действующую на пробную частицу:
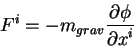
Гравитационный потенциал создается распределением масс и уравнение для
потенциала имеет вид уравнения типа скалярного поля. В отличие от
современных уравнений скалярного поля, уравнения ньютоновского
гравитационного поля не являются релятивистски инвариантными, поскольку
гравитационная теория Ньютона существенно нерелятивистская теория. Поэтому
уравнения поля есть уравнение типа Пуассона:
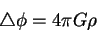 |
(9.1) |
Естественно, что ньютоновские уравнения гравитационного поля не могли
быть согласованы с принципами релятивистской физики. Потребовалось создание
новой теории гравитации - общей теории относительности.
После создания специальной теории относительности А.Эйнштейн начал
разработку идей связанных с распространением принципа относительности на
ускоренные системы отсчета. Достаточно скоро стало понятно, что невозможно
распространение принципа относительности на ускоренные системы отсчета без
обсуждения гравитационного поля.
Первая статья [15] относится лишь к однородноускоренным системам
координат. Однако уже там появляется идея - отождествление ускорения и
однородного гравитационного поля. Эта идея оказалась очень плодотворной и
решающей для обобщения принципа относительности - создания общей теории
относительности, которая включает в себя теорию релятивистского
гравитационного поля. Там же (параграф 19 этой статьи) А.Эйнштейн получает
связь между темпом течения времени в гравитационном поле с различным
потенциалом:
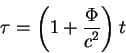
В следущем параграфе А.Эйнштейн делает вывод о том, что гравитационное поле
надо, по - видимому, характеризовать переменной скоростью света:
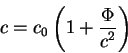
Следущую важную работу, посвященную гравитации, А.Эйнштейн опубликовал
только в 1912 г [16]. В ней он полемизирует с Абрагамом, который
построил свою теорию гравитации и строит теорию гравитации для случая
статического гравитационного поля. В этой статье все еще эксплуатируется
идея переменности скорости света. А.Эйнштейн ищет уравнение для случая
статического гравитационного поля, при этом руководствуется уравнением
нерелятивистского гравитационного поля. Он приходит к выводу, что уравнение
должно быть однородно по скорости света и приводит его в виде:
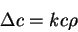
В следущей статье, опубликованной в том же 1912 году А.Эйнштейн учитывает
вклад энергии самого гравитационного поля в гравитационное поле и впервые
получает нелинейное уравнение вида:
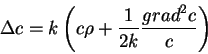
Уравнения гравитационного поля становятся нелинейными.
В следущем 1913 г. А.Эйнштейн в совместной статье с М.Гроссманом
[17] ясно формулирует связь гравитационного поля с метрическим
тензором 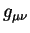 . Таким образом тензор второго ранга становится
величиной, которая описывает гравитационное поле. В этой же статье
окончательно появляется идея тождественности искривленного пространства -
времени и гравитации, появляется тензор кривизны и другие величины
свойственные для неэвклидовой геометрии. Там же делается попытка вывести
релятивистские уравнения гравитационного поля. . Таким образом тензор второго ранга становится
величиной, которая описывает гравитационное поле. В этой же статье
окончательно появляется идея тождественности искривленного пространства -
времени и гравитации, появляется тензор кривизны и другие величины
свойственные для неэвклидовой геометрии. Там же делается попытка вывести
релятивистские уравнения гравитационного поля.
Окончательно релятивистские уравнения гравитационного поля были выведены в
1916 г. В статье, опубликованной в "Анналах физики" [18],
А.Эйнштейн сформулировал общую теорию относительности, придал окончательный
вид уравнениям гравитационного поля, которыми мы пользуемся по сей день (а
также ввел знаменитое правило суммирования по повторяющимся индексам).
Весьма скоро после начала работы над общей теорией относительности,
А.Эйнштейн понял значение гамильтонова подхода для вывода уравнений поля.
Этот подход оказался очень плодотворным в современной теоретической физике.
Он связан с понятием экстремума действия и принципом наименьшего действия.
Именно таким образом мы и будем выводить уравнения гравитационного поля.
Уравнение (9.1) является существенно нерелятивистским
урапвнением. Это легко показать. Решением уравнения (9.1)
является интеграл:
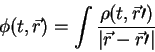
любые изменения в источнике (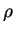 зависит от времени) могут быть мгновенно обнаружены (здесь мы опускаем проблемы связанные с обнаружением
сигнала) в тот же момент времени и на любом расстоянии от источника. Это
прямо противоречит постулату о невозможности передачи информации со
скоростью превышающей скорость света. зависит от времени) могут быть мгновенно обнаружены (здесь мы опускаем проблемы связанные с обнаружением
сигнала) в тот же момент времени и на любом расстоянии от источника. Это
прямо противоречит постулату о невозможности передачи информации со
скоростью превышающей скорость света.
Изменить это уравнение на релятивистское крайне просто. Необходимо добавить
вторую производную по времени, превратив уравнение Пуассона в уравнение
д'Аламбера:
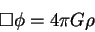 |
(9.2) |
Слева в уравнении теперь стоит релятивистски инвариантный оператор, который
обеспечивает релятивистскую инвариантность. Справа должен стоять источник
поля (плотность), обладающий такими же свойствами как и поле. Если поле
описывается скалярной величиной, то и источник поля также должен быть
скалярной величиной. Если гравитационное поле описывается тензором ранга
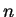 , то и источник должен быть тензором ранга , то и источник должен быть тензором ранга 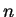 . .
Поскольку одноименные заряды в гравитации притягиваются ( в отличие от
электромагнитной теории, в которой одноименные заряды отталкиваются ), то
гравитационное поле должно описываться тензором четного ранга - скалярным
полем, полем тензора второго ранга и т.п. 9.1
Поэтому при релятивистском обобщении ньютоновской теории гравитации,
определяемой уравнением (9.2), необходимо определить
тензорные свойства источника поля. Величина 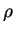 может быть
нерелятивистским пределом либо тензора энергии - импульса может быть
нерелятивистским пределом либо тензора энергии - импульса 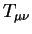 ,
либо скалярной величины - следа этого тензора ,
либо скалярной величины - следа этого тензора 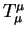 . В первом
случае гравитационное поле представляется тензором второго ранга, во втором
случае - тензором первого ранга. Эксперимент показывает, что справедлива
теория гравитации с полем второго ранга в качестве полевой переменной. . В первом
случае гравитационное поле представляется тензором второго ранга, во втором
случае - тензором первого ранга. Эксперимент показывает, что справедлива
теория гравитации с полем второго ранга в качестве полевой переменной.
Итак мы должны найти связь между метрическим тензором 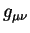 и
распределением масс, которая заменит уравнение (9.1) классической
ньютоновской теории тяготения. Рассмотрим вывод уравнений гравитационного
поля в общей теории относительности ( уравнений Эйнштейна ) используя
принцип наименьшего действия. Уравнения гравитационного поля получатся
вариацией действия по метрическому тензору - полевой переменной. Это
действие, как и для полей другого вида должно быть представлено в виде
некоторого скаляра, который является интегралом по 4 и
распределением масс, которая заменит уравнение (9.1) классической
ньютоновской теории тяготения. Рассмотрим вывод уравнений гравитационного
поля в общей теории относительности ( уравнений Эйнштейна ) используя
принцип наименьшего действия. Уравнения гравитационного поля получатся
вариацией действия по метрическому тензору - полевой переменной. Это
действие, как и для полей другого вида должно быть представлено в виде
некоторого скаляра, который является интегралом по 4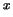 пространству от
некоторой скалярной плотности, зависящей от метрического тензора и первых
производных метрического тензора. Такой скалярной плотностью является
только величина: пространству от
некоторой скалярной плотности, зависящей от метрического тензора и первых
производных метрического тензора. Такой скалярной плотностью является
только величина:
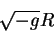
образуемая из скаляра кривизны. Действие 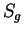 гравитационного поля можно,
следовательно, представить в виде: гравитационного поля можно,
следовательно, представить в виде:
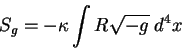 |
(9.3) |
Здесь 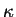 -некоторая новая гравитационная постоянная. Определить ее
связь с кавендишевой гравитационной постоянной с точностью до безразмерного
постоянного множителя достаточно просто - действие имеет размерность
энергии, скаляр кривизны имеет размерность см -некоторая новая гравитационная постоянная. Определить ее
связь с кавендишевой гравитационной постоянной с точностью до безразмерного
постоянного множителя достаточно просто - действие имеет размерность
энергии, скаляр кривизны имеет размерность см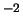 , а объем при
интегрировании см , а объем при
интегрировании см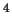 . Отсюда из соображений размерности находим, что . Отсюда из соображений размерности находим, что
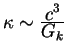 , где , где 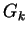 - гравитационная постоянная
Кавендиша. - гравитационная постоянная
Кавендиша.
Скалярная кривизна наряду с метрическим тензором и его первыми производными
содержит также и вторые производные от метрического тензора. Применяя к
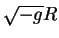 производную Эйлера - Лагранжа можно получить уравнеия
гравитационного поля. Прямые вычисления очень трудоемкие и содержат большое
количество выкладок. Мы несколько упростим вычисления, для чего
воспользуемся двумя свойствами скаляра кривизны. производную Эйлера - Лагранжа можно получить уравнеия
гравитационного поля. Прямые вычисления очень трудоемкие и содержат большое
количество выкладок. Мы несколько упростим вычисления, для чего
воспользуемся двумя свойствами скаляра кривизны.
Первый прием при выводе уравнений гравитационного поля впервые применили
[8]. Он основан на том, что в скалярной кривизне вторые производные
метрического тензора входят линейно, что позволяет выделить полную
дивергенцию, которая не влияет на уравнения движения. Поэтому действие
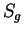 можно представить в виде: можно представить в виде:
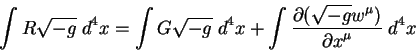
Слева стоит скалярная величина9.2. Справа стоят два
неинвариантных члена. Хотя их сумма является инвариантом, каждый из членов
неинвариантен. Для вывода уравнений поля нарушение инвариантности не
страшно, поскольку при выводе используются вариации этих величин. Напомним,
что вариации многих неинвариантных величин являются уже инвариантными,
пример, символ Кристоффеля не являются тензором, в то время как вариации
символа уже являются тензором третьего ранга.
Кроме того, полную дивергенцию по теореме Остраградского можно
преобразовать в интеграл по трехмерной гиперповерхности. При вычислении
вариаций этот член будет равен нулю, так как по определению вариации на
гиперповерхности, охватывающей объем равны нулю. Поэтому вариация
гравитационного действия равна:
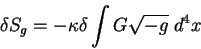
Найдем величину 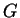 , которая определяет действие гравитационного поля и
вычислим ее вариацию относительно метрического тензора. , которая определяет действие гравитационного поля и
вычислим ее вариацию относительно метрического тензора.
Скалярная плотность кривизны выражается через метрический тензор и символы
Кристоффеля как:
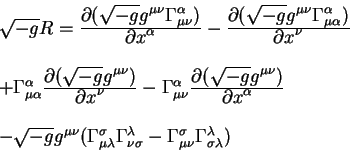
Находим величины
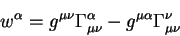
и
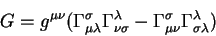
Производная Эйлера - Лагранжа величины 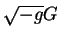 определяет уравнения
гравитационного поля. определяет уравнения
гравитационного поля.
Производная Эйлера - Лагранжа от величины 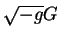 определяется как: определяется как:
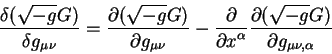
Как видно из определения, 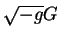 зависит от самого метрического
тензора зависит от самого метрического
тензора 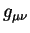 и символов Кристоффеля. Вычислим частные производные
от и символов Кристоффеля. Вычислим частные производные
от 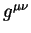 и и 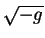 по метрическому тензору по метрическому тензору 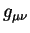 . .
Для вычисления частных производных от контравариантного метрического
тензора 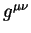 по ковариантному метрическому тензору по ковариантному метрическому тензору 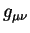 воспользуемся равенством вида:
воспользуемся равенством вида:
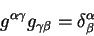
беря частную производную по ковариантному метрическому тензору по частям
получаем уравнение вида:
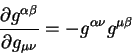
в этом уравнении достаточно трудно усмотреть симметрию по паре индексов
 и и  . Для того, чтобы сделать эту симметрию явной,
образуем симметричную сумму в правой части этого равенства, тогда частная
производная будет равна: . Для того, чтобы сделать эту симметрию явной,
образуем симметричную сумму в правой части этого равенства, тогда частная
производная будет равна:
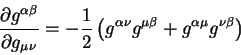
Для вычисления частной производной от корня из детерминанта 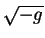 воспользуемся равенством:
воспользуемся равенством:
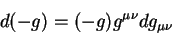
тогда получаем
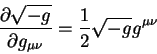
Частные производные от плотности действия 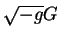 по ковариантному
метрическому тензору по ковариантному
метрическому тензору 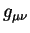 формируются только из частных
производных от контраваиантных компонент метрического тензора формируются только из частных
производных от контраваиантных компонент метрического тензора 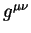 , которые входят в символы Кристоффеля и в определитель , которые входят в символы Кристоффеля и в определитель 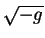 .
Производные от символа Кристоффеля есть: .
Производные от символа Кристоффеля есть:
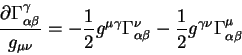
Выпишем теперь частную производную от плотности гравитационного действия
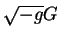 по метрическому тензору: по метрическому тензору:
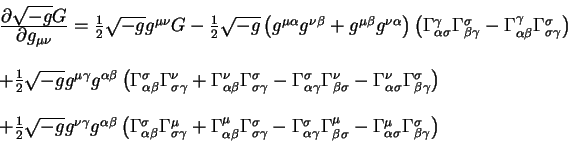
Несмотря на громоздкий вид структура этой формулы достаточна простая.
Более сложной является структура частной производной от
гравитационного действия по производной от метрического тензора.
Рассмотрим теперь ее.
Рассмотрим как происходит дифференцирование функции 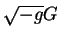 по
производной метрического тензора, скажем, по
производной метрического тензора, скажем, 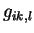 . Поскольку
производные от метрического тензора по координатам содержатся только в
символах Кристоффеля . Поскольку
производные от метрического тензора по координатам содержатся только в
символах Кристоффеля
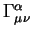 , то и частная
производная будет действовать только на эти члены. Только для этих
вычислений будем использовать латинские индексы в обозначениях
метрического тензора. Только в этом параграфе будем считать, что они
пробегают значения 0, 1, 2, 3. , то и частная
производная будет действовать только на эти члены. Только для этих
вычислений будем использовать латинские индексы в обозначениях
метрического тензора. Только в этом параграфе будем считать, что они
пробегают значения 0, 1, 2, 3.
Выпишем частную производную от символов Кристоффеля по нашей динамической
переменной - частной производной от метрического тензора по одной из
координат:
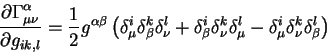
Подставим эту формулу в выражение для частной производной от плотности
гравитационного действия по нашей динамической переменной - частной
производной от метрического тензора по одной из координат
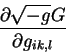
получим некоторое громоздкое выражение. Не выписывая его здесь целиком,
свернем по мертвым индексам суммирования, что значительно упростит запись:
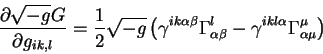
В этом уравнении введен новый тензор четвертого ранга
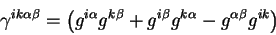
В производную Эйлера - Лагранжа член вида
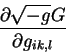
входит не самостоятельно, в от него вычисляется частная производная по
координате, которая стоит в динамической переменной - частной производной
от метрического тензора по координате
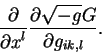
После вычисления частных производных по координате 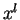 появляются
производные от символов Кристоффеля по координатам: появляются
производные от символов Кристоффеля по координатам:
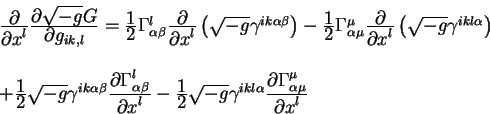
Частные производные от символов Кристоффеля входят в тензор кривизны. Этот
тензор имеет ранг 4. Но производные, которые появлись в приведенной выше
формуле входят в тензор Риччи. Запишем эту формулу через тензор Риччи
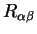 . .
Выражая частные производные от символов Кристоффеля через тензор Риччи
получим член в левой части равенства вида:
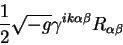
Выражая тензор
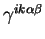 в виде произведений метрического
тензора и свертывая по индексам суммирования получаем член вида: в виде произведений метрического
тензора и свертывая по индексам суммирования получаем член вида:
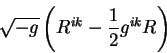
Оставшиеся четыре члена представляют произведения символов Кристоффеля,
окончательно выпишем производную от гравитационного действия в виде:
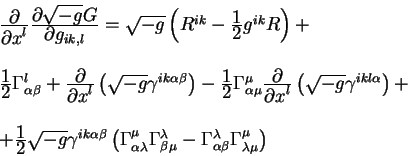
Выпишем окончательно производную Эйлера - Лагранжа от плотности
гравитационного действия:
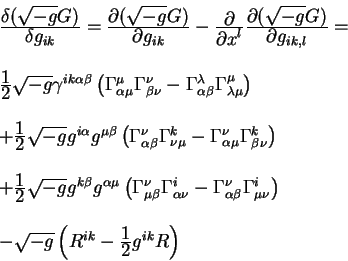
Для упрощения дальнейших выкладок выберем систему координат, в которой
удовлетворяется условие 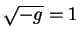 во всем пространстве - времени.
Поскольку это только одно условие, то его можно удовлетворить подходящим
выбором системы координат всегда. Доказательство этого утверждения не
входит в наш курс. Следствием этого выбора является уравнение: во всем пространстве - времени.
Поскольку это только одно условие, то его можно удовлетворить подходящим
выбором системы координат всегда. Доказательство этого утверждения не
входит в наш курс. Следствием этого выбора является уравнение:
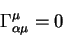
справедливое для любого значения индекса  . Тогда первый член в этом
уравнении обращается в нуль. . Тогда первый член в этом
уравнении обращается в нуль.
Подставим уравнение для производной Эйлера - Лагранжа в вариацию действия:
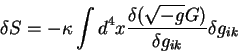
Свертка второго и третьего членов с вариацией метрического тензора
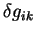 дает нуль, поскольку это сумма второго и третьего членов
антисимметрична по индексам дает нуль, поскольку это сумма второго и третьего членов
антисимметрична по индексам 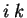 . В результате вариация гравитационного
действия по метрическому тензору равна: . В результате вариация гравитационного
действия по метрическому тензору равна:
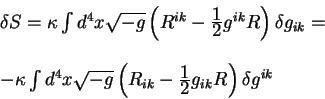
Заметим, что знак минус в последнем равенстве появляется, поскольку
вариации контравариантных компонент метрического тензора противоположна
вариациям ковариантных компонент:
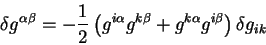
Из вариации действия гравитационного поля сразу можно получить
релятивистские уравнения поля в пустом пространстве:
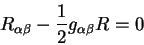 |
(9.4) |
Это уравнение эквивалентно уравнению:
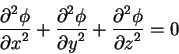
в ньютоновской теории гравитационного поля.
Вариация гравитационного действия вычислена в определенной системе
координат, которая удовлетворяет условию 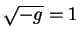 . Однако, уравнения
гравитационного поля получены в общековариантном виде, который справедлив
независимо от выбора системы координат. . Однако, уравнения
гравитационного поля получены в общековариантном виде, который справедлив
независимо от выбора системы координат.
Для вывода релятивистских уравнений, которые связывают гравитационное поле
и распределение материи необходимо найти величину, которая получается при
вариации плотности действия от материи по метрическому тензору.
Прежде чем перейти в выводу уравнений общей теории относительности, которые
связывают распределение гравитационного поля (метрического тензора) с
распределением материи приведем еще один вывод вариации действия
гравитационного поля, который является общековариантным и не требует
привлечения специальной системы координат. При этом, вывод уравнений
релятивистской гравитации методом Паллатини является экономным с точки
зрения выкладок.
Уже в предыдущем параграфе читатель мог обратить внимание на то, что вывод
уравнений гравитационного поля был отягощен многими предположениями, в
частности о выборе специальной системы координат. Это - необходимое
следствие общей ковариантности теории. Если в теории, например,
электромагнитного поля, вычисление амплитуд потенциала и их производных по
времени и координатам достаточно, чтобы полностью определить эволюцию поля,
то в общей теории относительности изменить значения метрического тензора и
его производных можно с помощью координатного преобразования. Координатное
преобразование метрического тензора не несет никакой физической нагрузки,
оно целиком зависит от соображений удобства вычислений. Поэтому необходимо
выделить ту часть в метрическом тензоре, которая обуславливает динамическую
эволюцию.
Эта проблема возникла потому, что в метрическим тензоре содержатся
дополнительные степени свободы для того, чтобы обеспечить правильное
поведение его компонент при координатных преобразованиях. Дополнительные
степени свободы подчиняются некоторым связям, которые необходимо учитывать
при выводе уравнений поля.
В современной теории поля разработан метод, который позволяет отделить
динамическую часть от части не несущей физической информации [20].
Этот формализм в современной теории поля называется каноническим. У него
есть два существенных свойства. Первое заключается в том, что уравнения
поля имеют первый порядок относительно производных по времени. Второе
свойство заключается в явнов выделении времени в лоренц - инвариантной
теории (так называемое 3+1 расщепление). В классической механике этот
формализм совпадает с формализмом Гамильтона.
Для получения этого формализма в общей теории относительности необходимо
записать плотность действия в линейном относительно первых производных
виде (этот вид называется записью в форме Паллатини). Обычный интеграл
действия:
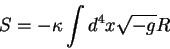
дает уравнения общей теории относительности при варьировании метрического
тензора 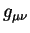 . Получившиеся уравнения Эйлера являются
дифференциальными уравнениями в частных производных второго порядка
относительно метрического тензора. Однако, те же уравнения можно привести к
каноническому гамильтонову виду: . Получившиеся уравнения Эйлера являются
дифференциальными уравнениями в частных производных второго порядка
относительно метрического тензора. Однако, те же уравнения можно привести к
каноническому гамильтонову виду:
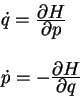
Для этого представим плотность лагранжиана гравитационного поля в форме
Палатини, при этом символы Кристоффеля рассматриваются как независимые
переменные:
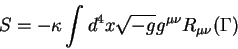 |
(9.5) |
где
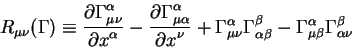
Здесь следует отметить, что ковариантные компоненты тензора Риччи не
содержат метрического тензора, а содержат только бинарные произведения
символов Кристоффеля и их производных по координатам. Варьируя
(9.5) по метрическому тензору получаем уравнения Эйнштейна:
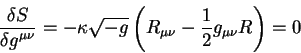 |
(9.6) |
Дополнительно к этим уравнениям получаем уравнения связи, которые
устанавливают соотношения между независимыми величинами 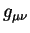 и и
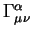 : :
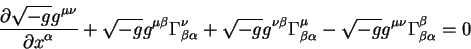
решая эти уравнения относительно величин
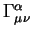 получаем обычную зависимость между символами Кристоффеля и метрическим
тензором:
получаем обычную зависимость между символами Кристоффеля и метрическим
тензором:
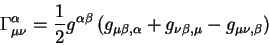
В предыдущем параграфе получены уравнения общей теории относительности в
вакууме. Полные уравнения должны содержать также влияние материи на
гравитационное поле. Они должны содержать источник гравитационного поля.
Полное действие для системы гравитационное поле + материя представляет из
себя сумму двух членов: действия для гравитационного поля 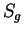 и действие
для материи и действие
для материи 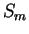 . Полные уравнения поля получаются как сумма вариаций
действия для поля и действия для материи: . Полные уравнения поля получаются как сумма вариаций
действия для поля и действия для материи:
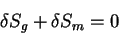
Вариации производятся по метрическому тензору, а сами уравнения получаются
из приравниванием к нулю первых производных Эйлера - Лагранжа от действия
по метрическому тензору:
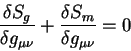 |
(9.7) |
Вариация от действия гравитационного поля по метрическому тензору есть
(9.6):
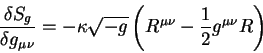
Вариации от  по метрическому тензору называются тензором энергии -
импульса: по метрическому тензору называются тензором энергии -
импульса:
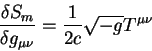 |
(9.8) |
Окончательно, уравнения гравитационного поля в общей теории относительности
имеют вид:
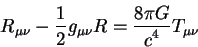 |
(9.9) |
Здесь постоянную
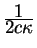 определяют из того условия, чтобы
в пределе слабых полей и медленных движений уравнения общей теории
относительности совпадали с уравнениями Ньютона для гравитационного поля. определяют из того условия, чтобы
в пределе слабых полей и медленных движений уравнения общей теории
относительности совпадали с уравнениями Ньютона для гравитационного поля.
Приведем несколько примеров тензора энергии - импульса.
Тензор энергии - импульса свободной частицы есть:
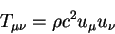 |
(9.10) |
Тензор энергии - импульса идеальной жидкости есть:
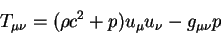 |
(9.11) |
Здесь 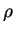 - плотность частицы в первом примере и плотность жидкости во
втором примере, - плотность частицы в первом примере и плотность жидкости во
втором примере, 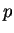 - давление в жидкости во втором примере. - давление в жидкости во втором примере.
<< 8. Уравнение движения в
| Оглавление |
Рекомендуемая и цитируемая литература >>
Посмотреть комментарии[8]
| 
