Задача об атоме водорода - одна из фундаментальных проблем квантовой механики, успешное решение которой способствовало дальнейшему развитию теории.
Атом водорода состоит из тяжелого ядра (протона массы 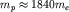 ) и движущегося в его кулоновском поле электрона. Сначала будем считать ядро бесконечно тяжелым, заменив его неподвижным кулоновским центром (конечность массы ядра учтем позже). Тогда гамильтониан атома можно записать в виде гамильтониана электрона в центральном поле: ) и движущегося в его кулоновском поле электрона. Сначала будем считать ядро бесконечно тяжелым, заменив его неподвижным кулоновским центром (конечность массы ядра учтем позже). Тогда гамильтониан атома можно записать в виде гамильтониана электрона в центральном поле:
,
где 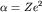 . Здесь Z - заряд ядра в единицах заряда электрона, причем Z=1 отвечает атому водорода H, а Z=2,3,... - водородоподобным ионам He+, Li++,... . Здесь Z - заряд ядра в единицах заряда электрона, причем Z=1 отвечает атому водорода H, а Z=2,3,... - водородоподобным ионам He+, Li++,...
Используя результаты п. 9, запишем волновую функцию стационарного состояния электрона, которая является собственной для полного набора наблюдаемых 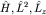 : :
.
Для радиальной функции  получаем уравнение получаем уравнение
.
Нетрудно показать, что при E>0 спектр гамильтониана непрерывен. В этом случае 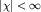 , но , но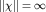 , что отвечает инфинитному движению электрона, и атом водорода как связанная система электрона и ядра не существует. Мы ограничимся поэтому рассмотрением дискретного спектра: E<0. , что отвечает инфинитному движению электрона, и атом водорода как связанная система электрона и ядра не существует. Мы ограничимся поэтому рассмотрением дискретного спектра: E<0.
Обозначим
и введем вместо r безразмерную переменную
.
Тогда уравнение на собственные значения примет вид:
,
введен параметр
.
Рассмотрим асимптотику ограниченного решения  . При . При 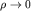 имеем (см. п. 9) имеем (см. п. 9)
.
При 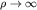 получаем приближенное уравнение получаем приближенное уравнение
,
откуда
.
Поэтому ищем решение в виде
.
Подставляя его в уравнение на СЗ, находим для функции v уравнение:
.
Решение ищем в виде ряда:
,
причем 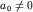 , чтобы обеспечить правильную асимптотику , чтобы обеспечить правильную асимптотику  при при 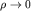 . Подставив ряд в уравнение, после очевидных замен индекса суммирования k получим: . Подставив ряд в уравнение, после очевидных замен индекса суммирования k получим:
.
Отсюда следует рекуррентное соотношение для коэффициентов ряда:
.
Ряд сходится при всех по признаку Даламбера: по признаку Даламбера:
.
Его асимптотическое поведение при больших  определяется коэффициентами ak при определяется коэффициентами ak при 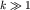 : :
,
откуда
,
т.е. для произвольного положительного параметра 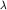 имеем при имеем при 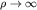 неприемлемую асимптотику радиальной функции: неприемлемую асимптотику радиальной функции:
.
Однако существуют такие дискретные значения 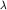 , при которых функция , при которых функция 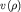 становится полиномом: становится полиномом:
.
Тогда 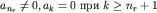 .
Вспомнив определение .
Вспомнив определение
,
приходим к дискретному спектру атома водорода и водородоподобных ионов:
.
Здесь введено главное квантовое число n, связанное с радиальным nr и орбитальным  квантовыми числами соотношением квантовыми числами соотношением
.
При заданном n орбитальное число  может принимать n значений: может принимать n значений:
.
Соответствующие волновые функции стационарных состояний имеют вид:
,
где
.
Полином 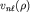 имеет степень имеет степень 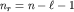 , равную числу его нулей (узлов). Коэффициенты ak при k>0 выражаются через a0 с помощью полученной выше рекуррентной формулы, а a0 определяется из условия нормировки: , равную числу его нулей (узлов). Коэффициенты ak при k>0 выражаются через a0 с помощью полученной выше рекуррентной формулы, а a0 определяется из условия нормировки:
.
Замечание. Можно показать, что 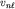 выражаются через обобщенные полиномы Лагерра выражаются через обобщенные полиномы Лагерра
,
и нормированная волновая функция имеет вид:
.
Мы видим, что собственные значения энергии вырождены с кратностью
.
Учет спина (две возможные проекции спинового момента на заданное направление) дает кратность dn=2n2, но спектр атома водорода в теории Паули не изменяется, так как отсутствует взаимодействие спинового магнитного момента с магнитным полем. Учет релятивистских эффектов (порядка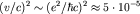 в атоме водорода) приводит к появлению тонкой структуры спектра. В частности, возникает спин-орбитальное взаимодействие в атоме водорода) приводит к появлению тонкой структуры спектра. В частности, возникает спин-орбитальное взаимодействие 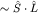 , т.е. взаимодействие спинового магнитного момента с внутриатомным магнитным полем, источником которого является орбитальное движение электрона. , т.е. взаимодействие спинового магнитного момента с внутриатомным магнитным полем, источником которого является орбитальное движение электрона.
Рассмотрим подробнее атом водорода (Z=1). Мы имеем атомную единицу длины
- боровский радиус (в полуклассической теории это радиус первой боровской орбиты: см. п. 1) и атомную единицу энергии - ридберг:
,
где R - постоянная Ридберга, входящая в выражение для спектральных частот излучения.
Энергия основного состояния атома водорода (главное квантовое число n=1) равна
.
Величина I=|E1| называется потенциалом ионизации. Он равен энергии связи электрона в атоме, определяемой как работа, которую нужно совершить, чтобы удалить электрон из атома.
Квантовая электродинамика (теория, объединяющая квантовую механику электрона и квантовую теорию электромагнитного поля на основе теории относительности) подтверждает гипотезу Бора о частотах спектральных линий:
.
Используя полученное выражение для En, приходим к известной формуле Бальмера (п.1):
.
Фиксируя n' и меняя n, получим различные спектральные серии. Укажем некоторые из них: n'=1 - серия Лаймана (ультрафиолетовая часть спектра излучения); n'=2 - серия Бальмера (первые 4 линии попадают в видимую часть спектра); n'=3 - серия Пашена (инфракрасная часть спектра).
Важные характеристики атома - вероятности переходов между стационарными состояниями wn'n. Они определяют интенсивности соответствующих спектральных линий, т.е. мощность излучения Wn'n на частоте 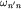 . Заметим, что величина . Заметим, что величина 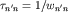 имеет смысл среднего времени жизни электрона на уровне En относительно перехода имеет смысл среднего времени жизни электрона на уровне En относительно перехода 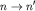 , или временного интервала, в течение которого испускается фотон с энергией , или временного интервала, в течение которого испускается фотон с энергией 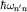 . Поэтому . Поэтому
.
Согласно квантовой электродинамике в главном (дипольном) приближении (малым параметром является отношение размера атома к длине волны испускаемого фотона) вероятность перехода выражается через матричные элементы rn'n оператора координаты электрона:
.
Здесь матричный элемент представляет собой интеграл, содержащий квадратичные комбинации волновых функций:
.
Для атома водорода индекс состояния n обозначает набор трех квантовых чисел (см. выше): 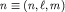 . Для некоторых переходов матричный элемент, а вместе с ним и интенсивность соответствующей спектральной линии, могут обращаться в нуль. Условия, при которых . Для некоторых переходов матричный элемент, а вместе с ним и интенсивность соответствующей спектральной линии, могут обращаться в нуль. Условия, при которых 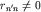 , называются правилами отбора.
Можно показать, что для атома водорода (и водородоподобных атомов) они имеют вид: , называются правилами отбора.
Можно показать, что для атома водорода (и водородоподобных атомов) они имеют вид:
,
причем 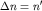 произвольно (1,2,...). Правила отбора выражают закон сохранения момента импульса при испускании фотона (спин его равен произвольно (1,2,...). Правила отбора выражают закон сохранения момента импульса при испускании фотона (спин его равен 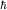 ) электроном. ) электроном.
Рассмотрим основное состояние атома водорода: 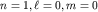 . Угловая
часть волновой функции . Угловая
часть волновой функции 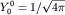 . Для радиальной части . Для радиальной части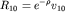 имеем
имеем 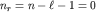 , т.е. v10 - полином нулевой степени. Учитывая связь , т.е. v10 - полином нулевой степени. Учитывая связь 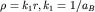 получаем полную функцию: получаем полную функцию:
.
Нормируем ее:
.
Итак, нормированная волновая функция основного состояния имеет вид:
.
Плотность вероятности обнаружить электрон на расстоянии r от ядра равна
.
Максимум вероятности достигается на расстоянии r=rm, определяемом из условия
.
Получаем в результате rm=aB.
Следовательно, радиус первой боровской орбиты - расстояние от ядра, на котором вероятность обнаружить электрон максимальна. Поскольку при 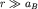 плотность экспоненциально мала, то можно сказать, что эффективный размер атома водорода порядка aB~ 10-8 см. плотность экспоненциально мала, то можно сказать, что эффективный размер атома водорода порядка aB~ 10-8 см.
Мы видим, что в основном состоянии распределение по координатам сферически симметрично. Это не так в возбужденных состояниях при 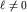 : :
.
Замечание. Угловое распределение вероятности универсально, т.е. одинаково для всех сферически-симметричных потенциалов (см. явный вид некоторых сферических функций 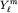 в п. 7). Что же касается вырождения уровней энергии по орбитальному числу в п. 7). Что же касается вырождения уровней энергии по орбитальному числу  , то оно характерно только для двух типов потенциалов U(r): кулоновского (U~1/r) и потенциала трехмерного осциллятора (U~r2). В.А. Фок (1935) показал, что "случайное" вырождение по , то оно характерно только для двух типов потенциалов U(r): кулоновского (U~1/r) и потенциала трехмерного осциллятора (U~r2). В.А. Фок (1935) показал, что "случайное" вырождение по  в кулоновском поле объясняется наличием более широкой, чем SO(3), группы симметрии SO(4). Это приводит к дополнительному интегралу движения в кулоновском поле объясняется наличием более широкой, чем SO(3), группы симметрии SO(4). Это приводит к дополнительному интегралу движения
,
причем ![$[\hat A,\hat L^2]\ne 0$](http://images.nature.web.ru/nature/2001/02/21/0001161226/tex/formula395.gif) .
Наблюдаемая .
Наблюдаемая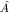 - аналог известного в классической механике вектора Рунге-Ленца, или вектора эксцентриситета: он направлен от фокуса эллиптической орбиты по большой оси к наиболее удаленной точке траектории, а его модуль равен эксцентриситету эллипса. - аналог известного в классической механике вектора Рунге-Ленца, или вектора эксцентриситета: он направлен от фокуса эллиптической орбиты по большой оси к наиболее удаленной точке траектории, а его модуль равен эксцентриситету эллипса.
Назад | Вперед
Посмотреть комментарии[1]
|

