Эта гипотеза состояла в том, что гладкий поток без положений
равновесия на трехмерной сфере
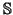 3 обязательно имеет
замкнутую траекторию. Основанием для этой гипотезы послужила теорема
Г.Зейферта, согласно которой замкнутая траектория имеется у всех
потоков, получающихся при малом возмущении ``потока Хопфа'', который
сейчас будет описан. 3 обязательно имеет
замкнутую траекторию. Основанием для этой гипотезы послужила теорема
Г.Зейферта, согласно которой замкнутая траектория имеется у всех
потоков, получающихся при малом возмущении ``потока Хопфа'', который
сейчас будет описан.
Реализуем трехмерную сферу
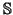 3 как множество тех точек
(z, w) двумерной комплексной плоскости 3 как множество тех точек
(z, w) двумерной комплексной плоскости
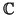 2 (с вещественной
точки зрения она четырехмерна), для которых
| z|2 + | w|2 = 1. Фазовая скорость потока Хопфа -- это векторное поле,
сопоставляющее точке (z, w) вектор (iz, iw). Траектории потока
Хопфа суть окружности
{eitz, eitw}; разбиение 2 (с вещественной
точки зрения она четырехмерна), для которых
| z|2 + | w|2 = 1. Фазовая скорость потока Хопфа -- это векторное поле,
сопоставляющее точке (z, w) вектор (iz, iw). Траектории потока
Хопфа суть окружности
{eitz, eitw}; разбиение
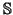 3
на эти окружности -- это известное в топологии расслоение
Хопфа 91,
откуда и название потока. Помимо доказательства, данного самим
Зейфертом, имеются по крайней мере два других доказательства его
теоремы, принадлежащие Ф.Б.Фуллеру и М.Боттколу (ссылки и
изложение идеи Фуллера см. в [78]). Фуллер использовал
``индекс Фуллера'' -- введенную им топологическую характеристику
поведения траекторий возле замкнутой траектории 92, а Ботткол --
своеобразный вариант теории возмущений (предложенный в одной работе
Ю.Мозера о периодических решениях возле положения равновесия); таким
образом, методы этих работ имеют более широкое значение (чего,
по-видимому, нельзя сказать о доказательстве самого Зейферта). Но они
тоже относятся только к малым возмущениям потока Хопфа. 3
на эти окружности -- это известное в топологии расслоение
Хопфа 91,
откуда и название потока. Помимо доказательства, данного самим
Зейфертом, имеются по крайней мере два других доказательства его
теоремы, принадлежащие Ф.Б.Фуллеру и М.Боттколу (ссылки и
изложение идеи Фуллера см. в [78]). Фуллер использовал
``индекс Фуллера'' -- введенную им топологическую характеристику
поведения траекторий возле замкнутой траектории 92, а Ботткол --
своеобразный вариант теории возмущений (предложенный в одной работе
Ю.Мозера о периодических решениях возле положения равновесия); таким
образом, методы этих работ имеют более широкое значение (чего,
по-видимому, нельзя сказать о доказательстве самого Зейферта). Но они
тоже относятся только к малым возмущениям потока Хопфа.
С гипотезой Зейферта связана ``гипотеза о торе'': если на
границе ``полнотория'' (``сплошного тора'')
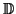 2× 2×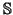 1 векторное поле фазовой скорости
направлено всюду внутрь (или всюду вовне) полнотория и в нем нет
положений равновесия, то в нем имеется замкнутая
траектория. Интуитивно кажется, что последняя должна, так сказать,
делать один оборот вдоль полнотория; поэтому построенный Фуллером
пример, когда, правда, имеется замкнутая траектория, но она гомотопна
нулю в полнотории, послужил ``тревожным сигналом'',
предостерегающим от доверия к наивной интуиции. 1 векторное поле фазовой скорости
направлено всюду внутрь (или всюду вовне) полнотория и в нем нет
положений равновесия, то в нем имеется замкнутая
траектория. Интуитивно кажется, что последняя должна, так сказать,
делать один оборот вдоль полнотория; поэтому построенный Фуллером
пример, когда, правда, имеется замкнутая траектория, но она гомотопна
нулю в полнотории, послужил ``тревожным сигналом'',
предостерегающим от доверия к наивной интуиции.
В настоящее время обе гипотезы опровергнуты даже для аналитических
потоков. В основном это заслуга К.Куперберг [108], [109],
построившей
C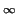 -контрпримеры, после чего У.Терстен и Э.Гис
указали аналитическую модификацию построения. Стоит отметить и вклад
предыдущих авторов. Ф.В.Вильсон построил контрпримеры к многомерным
аналогам гипотезы Зейферта. Это, в общем, не удивительно, -- довольно
понятно, что в многомерном случае квазипериодические траектории вполне
могут ``заменить'' периодическую, что и имеет место у Вильсона, --
однако часть его технических приемов пригодилась последующим авторам.
Неожиданностью был контрпример П.Швейцера 93(уже ``настоящий'', трехмерный) с потоком гладкости C1 (1974 г.).
После этого более гладкие варианты обоих гипотез не внушали большого
доверия, однако даже поднять гладкость в контрпримерах до C2
удалось далеко не сразу (Дж.Харрисон). -контрпримеры, после чего У.Терстен и Э.Гис
указали аналитическую модификацию построения. Стоит отметить и вклад
предыдущих авторов. Ф.В.Вильсон построил контрпримеры к многомерным
аналогам гипотезы Зейферта. Это, в общем, не удивительно, -- довольно
понятно, что в многомерном случае квазипериодические траектории вполне
могут ``заменить'' периодическую, что и имеет место у Вильсона, --
однако часть его технических приемов пригодилась последующим авторам.
Неожиданностью был контрпример П.Швейцера 93(уже ``настоящий'', трехмерный) с потоком гладкости C1 (1974 г.).
После этого более гладкие варианты обоих гипотез не внушали большого
доверия, однако даже поднять гладкость в контрпримерах до C2
удалось далеко не сразу (Дж.Харрисон).
Интересно, что, как доказал Х.Хофер, гипотеза Зейферта верна для
так называемых контактных потоков [111]. Контактные потоки бывают
на нечетномерных многообразиях
M2n + 1. Такой поток определяется
с помощью так называемой контактной формы 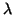 , т.е. пфаффовой
формы, для которой (2n + 1)-мерная форма , т.е. пфаффовой
формы, для которой (2n + 1)-мерная форма
всюду отлична от нуля. (Я опускаю уточнения о требуемой степени
гладкости 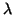 .) Это определение напоминает определение
симплектической структуры на четномерном многообразии 94,
но по существу здесь имеется по крайней мере одно существенное
различие. Задание симплектической формы никак не выделяет никаких
направлений в точках M. Контактная же форма в каждой точке x
определяет некоторое одномерное направление, -- именно, направление
вырождения формы d .) Это определение напоминает определение
симплектической структуры на четномерном многообразии 94,
но по существу здесь имеется по крайней мере одно существенное
различие. Задание симплектической формы никак не выделяет никаких
направлений в точках M. Контактная же форма в каждой точке x
определяет некоторое одномерное направление, -- именно, направление
вырождения формы d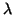 : вектор
X : вектор
X 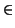 TxM имеет это
направление, если
d TxM имеет это
направление, если
d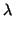 (X, Y) = 0 для любого Y (X, Y) = 0 для любого Y 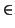 TxM.
Вдобавок фиксируется имеющий это направление вектор
Xx TxM.
Вдобавок фиксируется имеющий это направление вектор
Xx 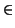 TxM, для
которого TxM, для
которого
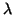 (Xx) = 1. Векторное поле X иногда называют полем
Ж.Риба. Контактный поток -- это поток с векторным полем фазовой
скорости X. (Xx) = 1. Векторное поле X иногда называют полем
Ж.Риба. Контактный поток -- это поток с векторным полем фазовой
скорости X.
В действительности теорема Хофера является более общей: если у
трехмерного замкнутого многообразия M одномерная группа когомологий
H1(M,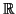 ) = 0, то любой контактный поток на M имеет
замкнутую траекторию. Это частный случай гипотезы А.Вайнстейна, в
которой многообразие не предполагается трехмерным. ) = 0, то любой контактный поток на M имеет
замкнутую траекторию. Это частный случай гипотезы А.Вайнстейна, в
которой многообразие не предполагается трехмерным.
Форму (32) можно принять за форму объема на M. (Для
читателя, который связывает понятие ``объем'' только с римановой
геометрией, замечу, что если на m-мерном гладком многообразии M
задана нигде не обращающаяся в нуль m-мерная внешняя форма 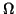 ,
то на M существует такая риманова метрика, для которой ``элемент
объема'' выражается как раз формой ,
то на M существует такая риманова метрика, для которой ``элемент
объема'' выражается как раз формой 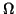 .) Легко доказать, что
контактный поток сохраняет задаваемый этой формой объем. Возникает
вопрос, не верна ли гипотеза Зейферта для любых потоков, сохраняющих
объем? Г.Куперберг (сын К.Куперберг) построил противоречащий пример к
этому предположению (ссылку см. в [109]). .) Легко доказать, что
контактный поток сохраняет задаваемый этой формой объем. Возникает
вопрос, не верна ли гипотеза Зейферта для любых потоков, сохраняющих
объем? Г.Куперберг (сын К.Куперберг) построил противоречащий пример к
этому предположению (ссылку см. в [109]).
Написать комментарий
|

