Next: 3 Теорема синусов
Up: Решение треугольников
Previous: 1 Теорема косинусов
Пусть опять в треугольнике известны стороны 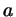 и и 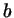 и угол
между ними и угол
между ними 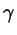 . Выразим через эти данные - которые
полностью определяют треугольник - его площадь. Для этого
опустим из вершины . Выразим через эти данные - которые
полностью определяют треугольник - его площадь. Для этого
опустим из вершины 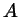 высоту высоту
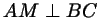 (рис. 60а);
пусть (рис. 60а);
пусть 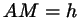 . Как известно, площадь треугольника равна . Как известно, площадь треугольника равна 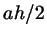 . .
Рис. 60:
Площадь треугольника.
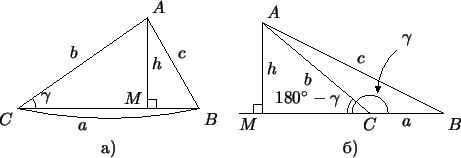 |
С другой стороны, если угол 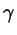 острый, то из прямоугольного
треугольника острый, то из прямоугольного
треугольника  находим, что находим, что
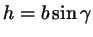 (рис. 60а); если же угол
(рис. 60а); если же угол 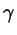 тупой
(рис. 60б), то из треугольника тупой
(рис. 60б), то из треугольника  опять же получаем опять же получаем
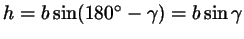 . Стало быть, в любом
случае площадь равна . Стало быть, в любом
случае площадь равна
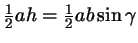 . .
Площадь треугольника равна
половине произведения двух его сторон на синус угла между
ними.
Мы пропустили случай, когда угол 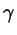 прямой. В этом случае прямой. В этом случае
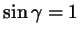 , и формула принимает вид , и формула принимает вид
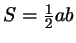 , что,
очевидно, справедливо. , что,
очевидно, справедливо.
Задача 2.1
Докажите, что площадь четырехугольника равна половине
произведения его диагоналей на синус угла между ними.
Задача 2.2
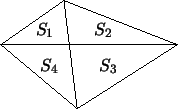
Диагонали четырехугольника делят его на четыре треугольника,
площади которых равны 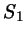 , , 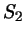 , , 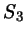 и и 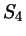 (рис. 61). Докажите, что
(рис. 61). Докажите, что
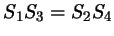 . .
Рис. 61:
 |
Итак, мы знаем, как находить площадь треугольника, если известны
две его стороны и угол между ними. А что делать, если даны три
стороны 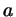 , , 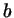 и и  ? Надо найти угол между сторонами ? Надо найти угол между сторонами 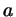 и и
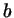 , благо мы это уже умеем. Точнее, нам нужен не сам угол, а его
синус. Его мы найдем так: из теоремы косинусов запишем , благо мы это уже умеем. Точнее, нам нужен не сам угол, а его
синус. Его мы найдем так: из теоремы косинусов запишем
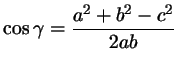 и воспользуемся формулой и воспользуемся формулой
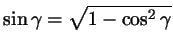 (для произвольных (для произвольных  , как
вы помните, в правой части может стоять минус, но если , как
вы помните, в правой части может стоять минус, но если
 - угол в пределах от - угол в пределах от 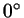 до до 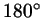 , то , то
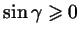 , так что в этом случае минус не нужен).
Подставляя все это в нашу формулу для площади треугольника,
получим вот что ( , так что в этом случае минус не нужен).
Подставляя все это в нашу формулу для площади треугольника,
получим вот что (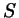 - площадь треугольника): - площадь треугольника):
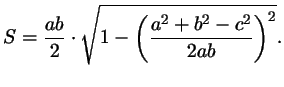 Это выражение можно преобразовать к более приятному виду. Для
этого обозначим буквой
Это выражение можно преобразовать к более приятному виду. Для
этого обозначим буквой 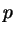 величину величину 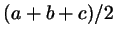 ( (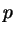 - половина
периметра треугольника, коротко - полупериметр). Тогда после
упрощений получим: - половина
периметра треугольника, коротко - полупериметр). Тогда после
упрощений получим:
Площадь треугольника со сторонами
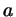 , , 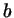 и и  равна равна
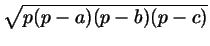 ,
где ,
где
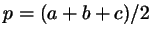 . .
Эта формула называется формулой Герона.
Задача 2.3
Проведите преобразования, с помощью которых из нашей формулы для
площади получается формула Герона.
Существует полезная формула, связывающая площадь
треугольника с радиусом вписанной в него окружности.
Именно, пусть 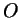 - центр окружности, вписанной в
треугольник - центр окружности, вписанной в
треугольник 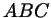 со сторонами со сторонами 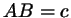 , , 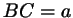 , , 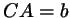 , , 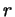 -
ее радиус. Расстояние от -
ее радиус. Расстояние от 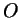 до каждой из сторон
треугольника равно, очевидно, до каждой из сторон
треугольника равно, очевидно, 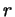 (рис. 62). (рис. 62).
Рис. 62:
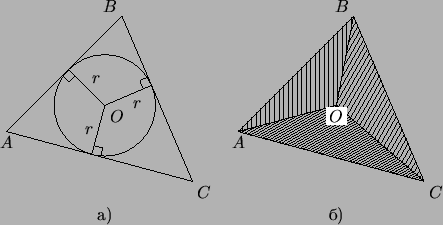 |
Поэтому, если разбить наш треугольник на треугольники  , ,
 и и  , то высоты, опущенные в них из точки , то высоты, опущенные в них из точки 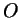 , все равны , все равны
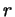 ; следовательно, площади этих треугольников равны ; следовательно, площади этих треугольников равны 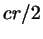 , ,
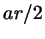 и и 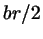 , а площадь всего треугольника , а площадь всего треугольника 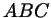 равна равна
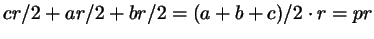 , где , где 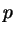 - полупериметр.
Словами: - полупериметр.
Словами:
Площадь треугольника равна
произведению его полупериметра на радиус
вписанной
окружности.
Задача 2.4
Даны стороны 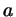 , , 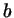 , ,  треугольника. Найдите:
а)
радиус вписанной окружности;
б)
высоту, опущенную на сторону треугольника. Найдите:
а)
радиус вписанной окружности;
б)
высоту, опущенную на сторону 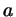 . .
Рис. 63:
 |
Задача 2.5. Пусть
стороны треугольника равны 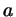 , , 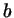 , ,  . Найдите радиус
окружности, касающейся стороны . Найдите радиус
окружности, касающейся стороны 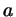 и продолжений сторон и продолжений сторон 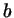 и и
 . (Окружность, касающаяся одной стороны треугольника и
продолжений двух других сторон, называется
вневписанной окружностью -
рис. 63.) . (Окружность, касающаяся одной стороны треугольника и
продолжений двух других сторон, называется
вневписанной окружностью -
рис. 63.)
Мы уже умеем находить медианы, площадь, высоты и радиус
Рис. 64:
Теорема о биссектрисе.
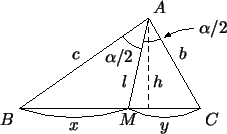 |
вписанной окружности треугольника по его трем сторонам (или по
двум сторонам и углу между ними). Давайте научимся находить и
биссектрису треугольника. Основным
средством у нас будет такая теорема:
Теорема. Если 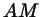 -
биссектриса угла -
биссектриса угла 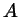 в треугольнике в треугольнике 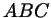 (рис. 64), то
(рис. 64), то
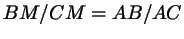 . Словами эту теорему можно
сформулировать так: ``биссектриса угла
в треугольнике делит противоположную сторону на части,
пропорциональные прилежащим сторонам''. . Словами эту теорему можно
сформулировать так: ``биссектриса угла
в треугольнике делит противоположную сторону на части,
пропорциональные прилежащим сторонам''.
Проще всего доказать эту теорему, используя площади. Именно,
обозначим 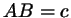 , , 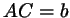 , , 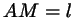 , ,
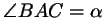 , , 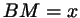 , ,
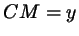 . Биссектриса . Биссектриса 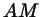 делит треугольник делит треугольник 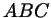 на два: на два: 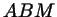 и и
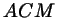 . Найдем двумя способами отношение их площадей.
Треугольники . Найдем двумя способами отношение их площадей.
Треугольники 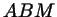 и и 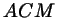 имеют общую высоту имеют общую высоту 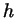 , поэтому их
площади пропорциональны основаниям: , поэтому их
площади пропорциональны основаниям:
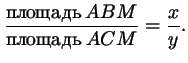 С другой стороны, так как
С другой стороны, так как 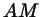 - биссектриса,
то - биссектриса,
то
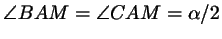 .
Пользуясь нашей формулой для площади, получаем: .
Пользуясь нашей формулой для площади, получаем:
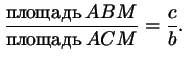 Сопоставляя два выражения для отношения площадей треугольников
Сопоставляя два выражения для отношения площадей треугольников
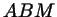 и и 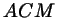 , получаем, что , получаем, что 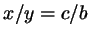 , или , или
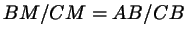 , что
и утверждалось. , что
и утверждалось.
Задача 2.6
а) В треугольнике со сторонами 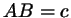 , , 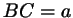 , , 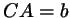 проведена биссектриса
проведена биссектриса 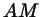 угла угла 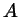 . Чему равны отрезки . Чему равны отрезки 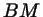 и и
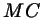 ? ?
б) В каком отношении точка пересечения биссектрис
делит биссектрису угла 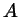 этого же треугольника? этого же треугольника?
Задача 2.7
Стороны треугольника равны 7, 8 и 12. Найдите длину
биссектрисы 8,
проведенной к стороне длиной 12.
Задача 2.8
В треугольнике биссектриса угла между сторонами длиной 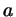 и и 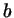 имеет длину
имеет длину 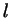 и делит противоположную сторону на отрезки длиной и делит противоположную сторону на отрезки длиной
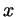 и и 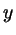 . Докажите формулу: . Докажите формулу:
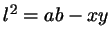 . .
Задача 2.9
В треугольнике 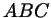 биссектриса угла, смежного к углу биссектриса угла, смежного к углу 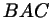 ,
пересекает прямую ,
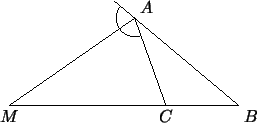
пересекает прямую 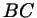 в точке в точке 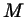 (рис. 65). Докажите, что (рис. 65). Докажите, что
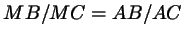 . .
Рис. 65:
 |
Задача 2.10
Высоты треугольника равны 2, 3 и 4. Найдите углы этого
треугольника.
Написать комментарий
|

