Next: 2 Вокруг площади треугольника
Up: Решение треугольников
Previous: Решение треугольников
Определения тригонометрических функций острых углов, которые мы
давали в начале нашей книжки, можно рассматривать как соотношения
между сторонами и углами прямоугольного треугольника. В этой
главе речь пойдет о произвольных треугольниках (не обязательно
прямоугольных). Ход мыслей будет вот каким. С каждым
треугольником связаны шесть чисел: величины трех сторон и трех
углов. Между этими числами есть соотношения. Одно из этих
соотношений вы уже знаете: сумма углов треугольника равна
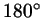 . Если, например, два угла в треугольнике равны . Если, например, два угла в треугольнике равны
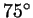 и и 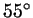 , то третий угол уже не может быть каким
попало, он обязательно равен , то третий угол уже не может быть каким
попало, он обязательно равен
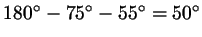 . Этим соотношением, однако, дело не исчерпывается.
Пусть, например, у некоторого треугольника мы знаем величины двух
сторон и угла между ними. Тогда, согласно одному из
признаков равенства
треугольников, оставшаяся сторона и остальные два угла уже
полностью определены. Наша цель - найти формулы, по которым они
выражаются через уже известные стороны и угол. . Этим соотношением, однако, дело не исчерпывается.
Пусть, например, у некоторого треугольника мы знаем величины двух
сторон и угла между ними. Тогда, согласно одному из
признаков равенства
треугольников, оставшаяся сторона и остальные два угла уже
полностью определены. Наша цель - найти формулы, по которым они
выражаются через уже известные стороны и угол.
Другие признаки равенства треугольников также ведут к
соотношениям между сторонами и углами, и эти соотношения также
можно задать формулами. Кроме того, если известны стороны и углы
треугольника, то этим однозначно определяются площадь
треугольника, радиусы вписанной и описанной окружности и тому
подобное. Для них тоже имеет смысл поискать формулы, выражающие
их через стороны и углы треугольника.
Начнем же мы как раз с соотношения, связанного
с ``первым признаком
равенства треугольников'' (по двум сторонам и углу между
ними) 6. Итак, пусть заданы две стороны 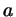 и и 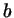 треугольника
и угол треугольника
и угол 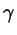 между ними. Попробуем выразить через эти данные
длину третьей стороны. Обозначим эту сторону между ними. Попробуем выразить через эти данные
длину третьей стороны. Обозначим эту сторону  . План действий
таков: . План действий
таков:
Рис. 58:
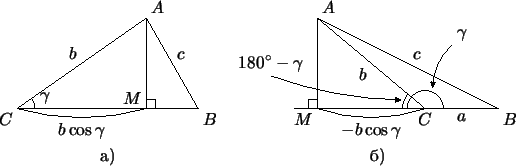 |
опустим высоту
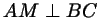 (рис. 58а - чертеж для
случая, когда угол (рис. 58а - чертеж для
случая, когда угол 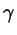 острый, 58 - для случая,
когда он тупой). По теореме Пифагора для треугольника острый, 58 - для случая,
когда он тупой). По теореме Пифагора для треугольника 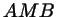 имеем имеем
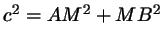 ; если мы теперь выразим ; если мы теперь выразим 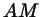 и и 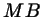 через
известные нам через
известные нам 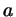 , , 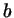 и и 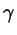 , то задача будет решена. Теперь
конкретно: , то задача будет решена. Теперь
конкретно:
- Пусть угол
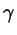 острый (рис. 58а).
Тогда: острый (рис. 58а).
Тогда:
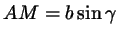 (из прямоугольного треугольника (из прямоугольного треугольника 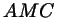 ); );
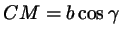 (из того же треугольника); (из того же треугольника);
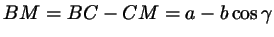 . .
Теперь по теореме Пифагора
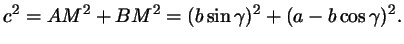 После упрощений, которые предоставляем вам провести
самостоятельно, получаем:
После упрощений, которые предоставляем вам провести
самостоятельно, получаем:
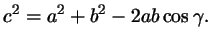
- Пусть угол
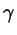 тупой (рис. 58б).
Тогда: тупой (рис. 58б).
Тогда:
(мы воспользовались формулами приведения). Отсюда
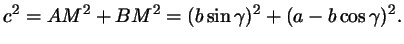 Получилось то же самое выражение, что и в первом случае; тем самым
для всех случаев мы доказали такую формулу:
Получилось то же самое выражение, что и в первом случае; тем самым
для всех случаев мы доказали такую формулу:
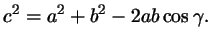
Эта формула называется теоремой
косинусов.
В нашем доказательстве мы не рассмотрели случай, когда
угол 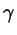 прямой. В этом случае теорема косинусов также верна
и, более того, была вам уже известна: если прямой. В этом случае теорема косинусов также верна
и, более того, была вам уже известна: если
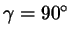 , то , то
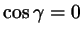 , и теорема косинусов приобретает вид , и теорема косинусов приобретает вид
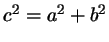 , то есть сводится к обычной
теореме Пифагора. , то есть сводится к обычной
теореме Пифагора.
Итак, часть программы по переводу первого признака равенства
треугольников на язык формул мы выполнили: формула для вычисления
третьей стороны по двум сторонам и углу между ними у нас уже
есть. Надо еще найти два оставшихся угла треугольника, при том
что один из углов и все стороны мы уже знаем. Собственно говоря,
угол даже и не нужен:
``третий признак
равенства треугольников'' гласит, что треугольник полностью
определяется своими тремя сторонами 7.
Стало быть, зададимся такой задачей: даны три стороны
треугольника, найти его углы. Оказывается, ее решение дает
та же теорема косинусов: надо только в формуле, выражающей
эту теорему, выразить
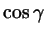 через через 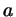 , , 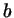 и и  : :
Вторая и третья формулы получаются аналогично первой.
Мы нашли не сами углы, а только их косинусы, но углы треугольника
этим полностью определяются: когда 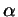 меняется от меняется от 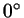 до
до 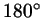 (то есть от 0 до (то есть от 0 до 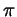 радиан), значение радиан), значение
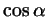 изменяется от 1 до изменяется от 1 до 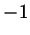 , принимая каждое значение
ровно один раз. Таким образом, можно записать: , принимая каждое значение
ровно один раз. Таким образом, можно записать:

Задача 1.1
В треугольнике со сторонами 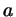 , , 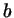 и и  против стороны против стороны  лежит угол
лежит угол 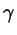 . Докажите, что угол . Докажите, что угол 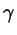 острый тогда и
только тогда, когда острый тогда и
только тогда, когда
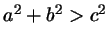 , и тупой тогда и только тогда,
когда , и тупой тогда и только тогда,
когда
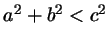 . .
Рис. 59:
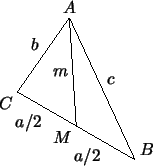 |
С помощью теоремы косинусов легко получить формулу, выражающую
длину медианы треугольника через
длины его сторон. Именно, пусть стороны треугольника равны
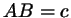 , , 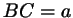 , , 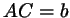 , и пусть , и пусть 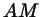 - медиана, проведенная
к стороне - медиана, проведенная
к стороне 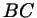 . Чтобы найти ее длину, заметим, что по теореме
косинусов для треугольника . Чтобы найти ее длину, заметим, что по теореме
косинусов для треугольника 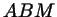 (рис. 59) имеем (рис. 59) имеем
С другой стороны, по теореме косинусов уже для всего треугольника
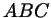 имеем имеем
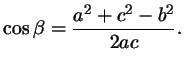 Подставляя это в предыдущую формулу, получим
(после упрощений) вот что:
Подставляя это в предыдущую формулу, получим
(после упрощений) вот что:
В треугольнике со сторонами 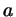 , , 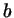 и и  длина медианы,
проведенной к стороне длина медианы,
проведенной к стороне 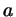 , равна , равна
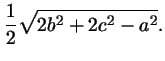
В задаче 1.4 мы предложим другой способ вывода этой
формулы.
Задача 1.2
Докажите что сумма квадратов диагоналей параллелограмма
равна сумме квадратов его сторон.
Задача 1.3
Две стороны треугольника равны 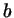 и и  , угол между ними равен , угол между ними равен
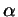 . Докажите, что длина медианы, проведенной к третьей
стороне, равна . Докажите, что длина медианы, проведенной к третьей
стороне, равна
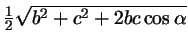 . .
Указание. Достройте треугольник до параллелограмма.
Задача 1.4
Используя результат задачи 1.2, дайте новое
доказательство формулы, выражающей медиану треугольника через три
его стороны.
Задача 1.5
В треугольнике 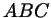 даны стороны даны стороны 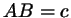 , , 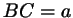 , ,
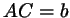 . Точка . Точка 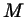 выбрана на стороне выбрана на стороне 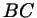 таким образом, что таким образом, что
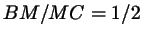 . Найдите длину отрезка . Найдите длину отрезка 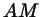 . .
Написать комментарий
|

