Механика твердого тела. Лекции.
В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)Издательство Физического факультета МГУ, 1997 г. Содержание
Центр удара.
Опыт показывает, что если тело, закрепленное на оси вращения, испытывает удар, то действие удара в общем случае передается и на ось. При этом величина и направление силы, приложенной к оси, зависят от того, в какую точку тела нанесен удар.
Рассмотрим сплошной однородный стержень АВ, подвешенный в точке А на горизонтальной, закрепленной в подшипниках оси OO' (рис. 3.9). Если удар (короткодействующая сила F ( нанесен близко к оси вращения, то ось прогибается в направлении действия силы F (рис. 3.9а). Если удар нанесен по нижнему концу стержня, вблизи точки В, то ось прогибается в противоположном направлении (рис. 3.9б). Наконец, если удар нанесен в строго определенную точку стержня, называемую центром удара (рис. 3.9в, точка С), то ось не испытывает никаких дополнительных нагрузок, связанных с ударом. Очевидно, в этом случае скорость поступательного движения, приобретаемого точной А вместе с центром масс O, будет компенсироваться линейной скоростью вращательного движения вокруг центра масс О (оба эти движения инициируются силой F и происходят одновременно).
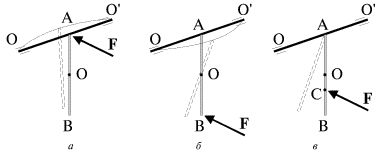 |
| Рис. 3.9. |
Вычислим, на каком расстоянии ![]() от точки подвеса стержня находится
центр удара. Уравнение моментов относительно оси вращения OO' дает
от точки подвеса стержня находится
центр удара. Уравнение моментов относительно оси вращения OO' дает
| (3.15) |
Сил реакции со стороны оси, как предполагается, при ударе не возникает, поэтому на основании теоремы о движении центра масс можно записать
| (3.16) |
где ![]() - масса тела,
- масса тела, ![]() - скорость центра масс. Если
- скорость центра масс. Если ![]() - расстояние
от оси до центра масс тела, то
- расстояние
от оси до центра масс тела, то
| (3.17) |
и в результате из уравнения моментов и уравнения движения центра масс находим
| (3.18) |
При этом точка C (центр удара) совпадает с так называемым центром качания данного физического маятника - точкой, где надо сосредоточить всю массу твердого тела, чтобы полученный математический маятник имел такой же период колебаний, как и данный физический.
В случае сплошного однородного стержня длиной ![]() имеем:
имеем:
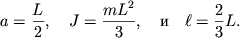 |
Замечание. Полученное выражение для ![]() (3.18) справедливо и для
произвольного твердого тела. При этом надо только иметь в виду, что точка
подвеса тела А и центр масс О должны лежать на одной вертикали, а ось
вращения должна совпадать с одной из главных осей инерции тела, проходящих
через точку А.
(3.18) справедливо и для
произвольного твердого тела. При этом надо только иметь в виду, что точка
подвеса тела А и центр масс О должны лежать на одной вертикали, а ось
вращения должна совпадать с одной из главных осей инерции тела, проходящих
через точку А.
Пример 1. При ударах палкой длиной ![]() по препятствию рука "не
чувствует" удара (не испытывает отдачи) в том случае, если удар приходится в
точку, расположенную на расстоянии
по препятствию рука "не
чувствует" удара (не испытывает отдачи) в том случае, если удар приходится в
точку, расположенную на расстоянии ![]() свободного конца палки.
свободного конца палки.
Пример 2. При горизонтальном ударе кием по бильярдному шару (рис. 3.10) шар начинает качение без проскальзывания в том случае, еcли удар нанесен в точку, находящуюся на высоте
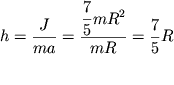 |
от поверхности бильярда, то есть на ![]() выше центра
шара. Если удар будет нанесен ниже, качение будет сопровождаться скольжением
в направлении движении шара. Если удар нанесен выше, то шар в точке касания
с бильярдным столом будет проскальзывать назад.
выше центра
шара. Если удар будет нанесен ниже, качение будет сопровождаться скольжением
в направлении движении шара. Если удар нанесен выше, то шар в точке касания
с бильярдным столом будет проскальзывать назад.
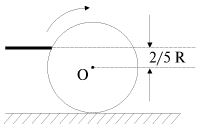 |
| Рис. 3.10. |
Рассмотренные примеры формально не относятся к вращению твердого тела вокруг неподвижной оси, однако все приведенные выше соображения о центре удара, очевидно, остаются в силе и в этих случаях.
II. Плоское движение твердого тела.
Напомним, что при плоском движении все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости, поэтому достаточно рассмотреть движение одного из сечения тела, например, того, в котором лежит центр масс. При разложении плоского движения на поступательное и вращательное скорость поступательного движения определена неоднозначно - она зависит от выбора оси вращения, однако угловая скорость вращательного движения оказывается одной и той же (см. лекцию 1).
Если в качестве оси вращения выбрать ось, проходящую через центр масс, то уравнениями движения твердого тела будут:
1. Уравнение движения центра масс
| (3.19) |
2. Уравнение моментов относительно оси, проходящей через центр масс
| (3.20) |
Особенностью плоского движения является то, что ось вращения сохраняет свою ориентацию в пространстве и остается перпендикулярной плоскости, в которой движется центр масс. Еще раз подчеркнем, что уравнение моментов (3.20) записано относительно, в общем случае, ускоренно движущегося центра масс, однако, как было отмечено в начале лекции, оно имеет такой же вид, как и уравнение моментов относительно неподвижной точки.
В качестве примера рассмотрим задачу о скатывании цилиндра с наклонное плоскости. Приведем два способа решения этой задачи с использованием уравнений динамики твердого тела.
Первый способ. Рассматривается вращение цилиндра относительно оси, проходящее через центр масс (рис. 3.11).
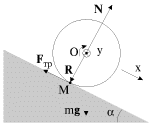 |
| Рис. 3.11. |
Система уравнений (3.19 - 3.20) имеет вид:
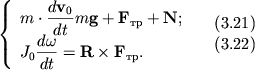 |
К этой системе необходимо добавить уравнение кинематической связи
| (3.23) |
Последнее уравнение получается из условия, что цилиндр скатывается без проскальзывания, то есть скорость точки М цилиндра равна нулю.
Уравнение движения центра масс (3.1) запишем для проекций ускорения и сил на ось x вдоль наклонной плоскости, а уравнение моментов (3.22) - для проекций углового ускорения и момента силы трения на ось y , совпадающую с осью цилиндра. Направления осей x и у выбраны согласованно, в том смысле, что положительному линейному ускорению оси цилиндра соответствует положительное же угловое ускорение вращения вокруг этой оси. В итоге получим:
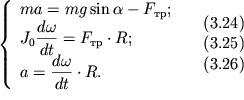 |
откуда
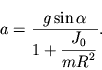 | (3.27) |
Следует подчеркнуть, что ![]() - сила трения сцепления - может
принимать любое значение в интервале от О до
- сила трения сцепления - может
принимать любое значение в интервале от О до ![]() (сила трения скольжения) в зависимости от
параметров задачи. Работу эта сила не совершает, но обеспечивает ускоренное
вращение цилиндра при его скатывании с наклонной плоскости. В данном случае
(сила трения скольжения) в зависимости от
параметров задачи. Работу эта сила не совершает, но обеспечивает ускоренное
вращение цилиндра при его скатывании с наклонной плоскости. В данном случае
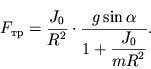 | (3.28) |
Если цилиндр сплошной, то
| (3.29) |
Качение без проскальзывания определяется условием
| (3.30) |
где ![]() - коэффициент трения скольжения,
- коэффициент трения скольжения, ![]() - сила реакции
опоры. Это условие сводится к следующему:
- сила реакции
опоры. Это условие сводится к следующему:
| (3.31) |
или
| (3.32) |
Второй способ. Рассматривается вращение цилиндра относительно неподвижной оси, совпадающей в данный момент времени с мгновенной осью вращения (рис. 3.12).
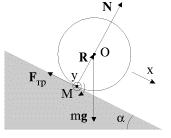 |
| Рис. 3.12. |
Мгновенная ось вращения проходит через точку соприкосновения цилиндра и плоскости (точку М). При таком подходе отпадает необходимость в уравнении движении центра масс и уравнении кинематической связи. Уравнение моментов относительно мгновенной оси имеет вид:
| (3.33) |
Здесь
| (3.34) |
В проекции на ось вращения (ось y)
| (3.35) |
Ускорение центра масс выражается через угловое ускорение
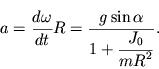 | (3.36) |
|
Публикации с ключевыми словами:
механика - твердое тело - углы Эйлера
Публикации со словами: механика - твердое тело - углы Эйлера | |
|
См. также:
| |